R平方/相关性取决于预测变量的方差

原文链接：http://tecdat.cn/?p=6289

 在我今天参与的一个讨论中，提出了一个问题，即在具有单个连续预测器的线性回归模型中R平方如何/是否取决于预测变量的方差。这个问题的答案当然是肯定的。

 可视化 

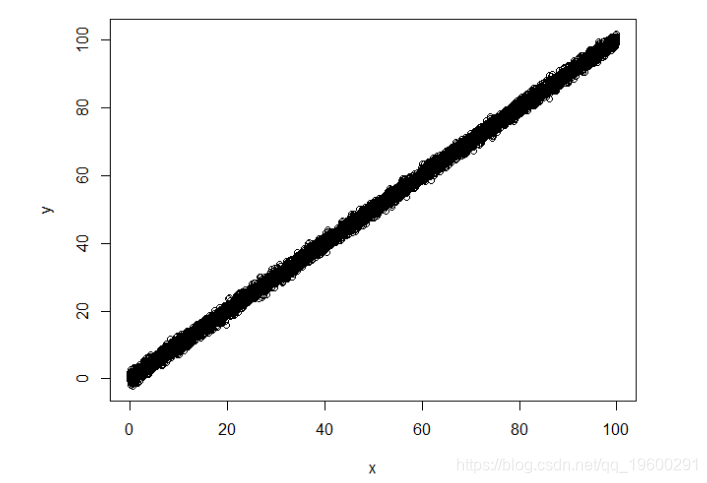
我们还可以在R中轻松地可视化前面的概念。我们首先从具有非常大的样本大小的线性模型中模拟数据：

n < -  10000
 x < -  100 * runif（n）
y < -  x + rnorm（n）

我们有：​

Y对X，对X没有限制

 拟合相应的线性模型证实了这一点：

summary(lm(y~x))

Call:
lm(formula = y ~ x)

Residuals:
    Min      1Q  Median      3Q     Max 
-4.1295 -0.6794 -0.0023  0.6879  3.5579 

Coefficients:
             Estimate Std. Error  t value Pr(>|t|)    
(Intercept) 0.0068489  0.0204500    0.335    0.738    
x           0.9999752  0.0003534 2829.539   <2e-16 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 1.015 on 9998 degrees of freedom
Multiple R-squared:  0.9988,	Adjusted R-squared:  0.9988 
F-statistic: 8.006e+06 on 1 and 9998 DF,  p-value: < 2.2e-16

给出R平方0.9988。

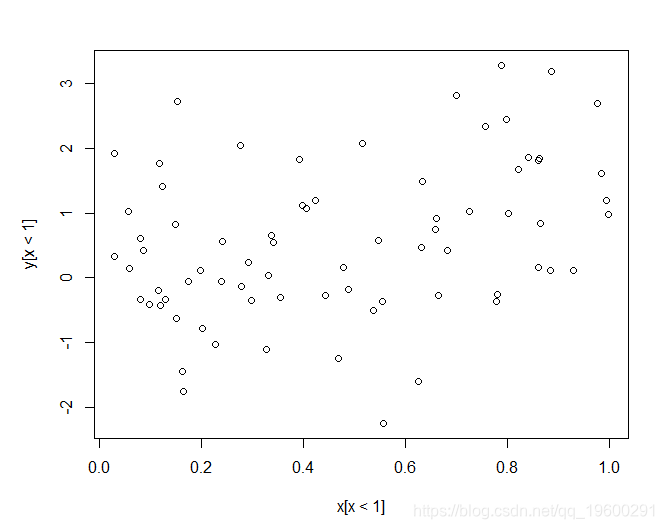
接下来，我们再次绘制数据， ​

summary(lm(y[x<1]~x[x<1]))

Call:
lm(formula = y[x < 1] ~ x[x < 1])

Residuals:
     Min       1Q   Median       3Q      Max 
-2.93421 -0.73513 -0.09459  0.69282  2.59506 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)   
(Intercept)  -0.0893     0.2432  -0.367  0.71459   
x[x < 1]      1.3960     0.4386   3.183  0.00215 **
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 1.121 on 72 degrees of freedom
Multiple R-squared:  0.1233,	Adjusted R-squared:  0.1112 
F-statistic: 10.13 on 1 and 72 DF,  p-value: 0.002155

R平方值低得多，为0.1233。

 

如果您有任何疑问，请在下面发表评论。