原文链接:http://tecdat.cn/?p=5453
变量选择方法
所有可能的回归
model <- lm(mpg ~ disp + hp + wt + qsec, data = mtcars)
ols_all_subset(model)
## # A tibble: 15 x 6
## Index N Predictors `R-Square` `Adj. R-Square` `Mallow's Cp`
##
## 1 1 1 wt 0.75283 0.74459 12.48094
## 2 2 1 disp 0.71834 0.70895 18.12961
## 3 3 1 hp 0.60244 0.58919 37.11264
## 4 4 1 qsec 0.17530 0.14781 107.06962
## 5 5 2 hp wt 0.82679 0.81484 2.36900
## 6 6 2 wt qsec 0.82642 0.81444 2.42949
## 7 7 2 disp wt 0.78093 0.76582 9.87910
## 8 8 2 disp hp 0.74824 0.73088 15.23312
## 9 9 2 disp qsec 0.72156 0.70236 19.60281
## 10 10 2 hp qsec 0.63688 0.61183 33.47215
## 11 11 3 hp wt qsec 0.83477 0.81706 3.06167
## 12 12 3 disp hp wt 0.82684 0.80828 4.36070
## 13 13 3 disp wt qsec 0.82642 0.80782 4.42934
## 14 14 3 disp hp qsec 0.75420 0.72786 16.25779
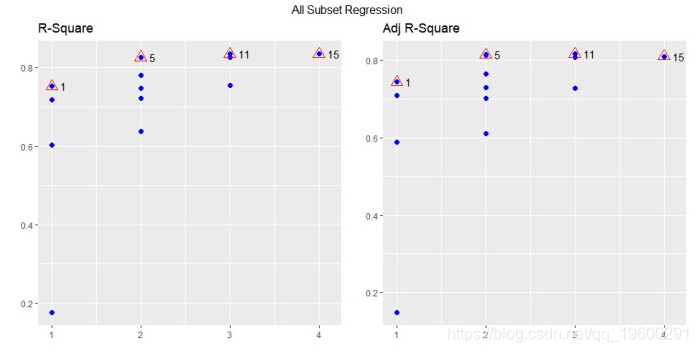
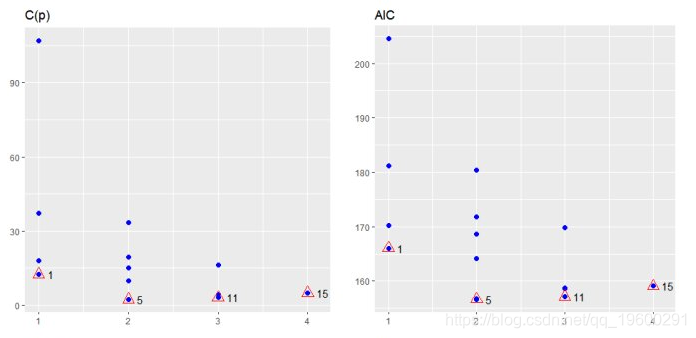
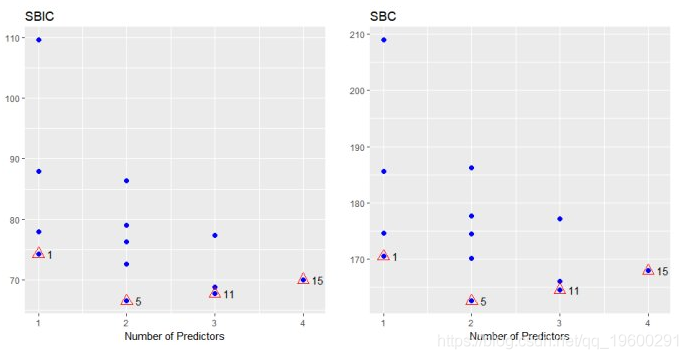
## 15 15 4 disp hp wt qsec 0.83514 0.81072 5.00000该plot方法显示了所有可能的回归方法的拟合 。
model <- lm(mpg ~ disp + hp + wt + qsec, data = mtcars)
k <- ols_all_subset(model)
plot(k)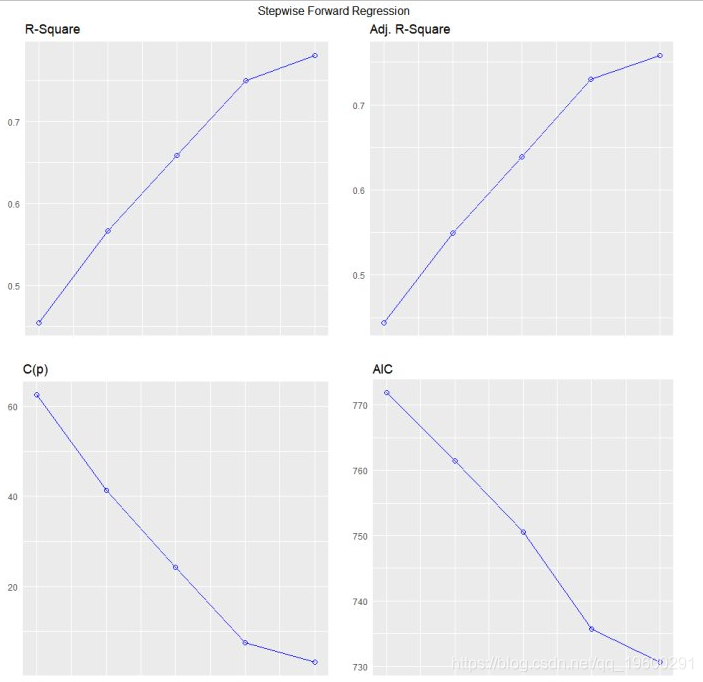
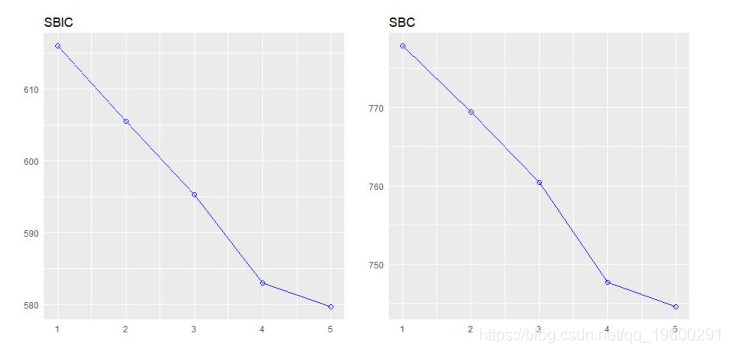
最佳子集回归
选择在满足一些明确的客观标准时做得最好的预测变量的子集,例如具有最大R2值或最小MSE, Cp或AIC。
model <- lm(mpg ~ disp + hp + wt + qsec, data = mtcars)
ols_best_subset(model)
## Best Subsets Regression
## ------------------------------
## Model Index Predictors
## ------------------------------
## 1 wt
## 2 hp wt
## 3 hp wt qsec
## 4 disp hp wt qsec
## ------------------------------
##
## Subsets Regression Summary
## -------------------------------------------------------------------------------------------------------------------------------
## Adj. Pred
## Model R-Square R-Square R-Square C(p) AIC SBIC SBC MSEP FPE HSP APC
## -------------------------------------------------------------------------------------------------------------------------------
## 1 0.7528 0.7446 0.7087 12.4809 166.0294 74.2916 170.4266 9.8972 9.8572 0.3199 0.2801
## 2 0.8268 0.8148 0.7811 2.3690 156.6523 66.5755 162.5153 7.4314 7.3563 0.2402 0.2091
## 3 0.8348 0.8171 0.782 3.0617 157.1426 67.7238 164.4713 7.6140 7.4756 0.2461 0.2124
## 4 0.8351 0.8107 0.771 5.0000 159.0696 70.0408 167.8640 8.1810 7.9497 0.2644 0.2259
## -------------------------------------------------------------------------------------------------------------------------------
## AIC: Akaike Information Criteria
## SBIC: Sawa's Bayesian Information Criteria
## SBC: Schwarz Bayesian Criteria
## MSEP: Estimated error of prediction, assuming multivariate normality
## FPE: Final Prediction Error
## HSP: Hocking's Sp
## APC: Amemiya Prediction Criteriaplot
model <- lm(mpg ~ disp + hp + wt + qsec, data = mtcars)
k <- ols_best_subset(model)
plot(k)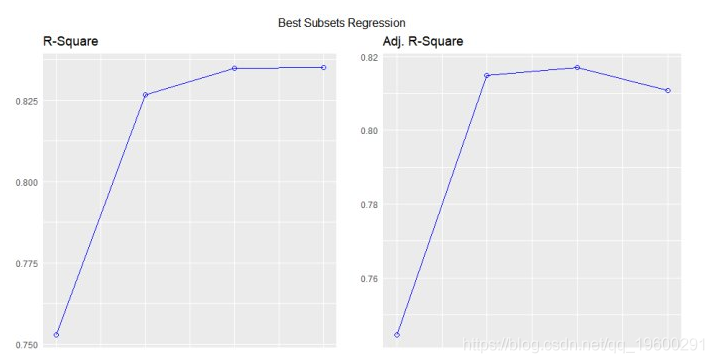
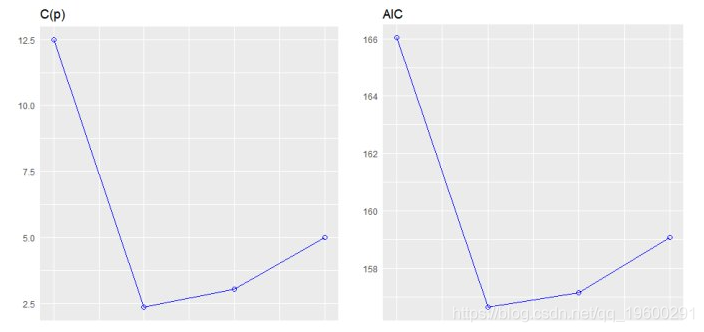
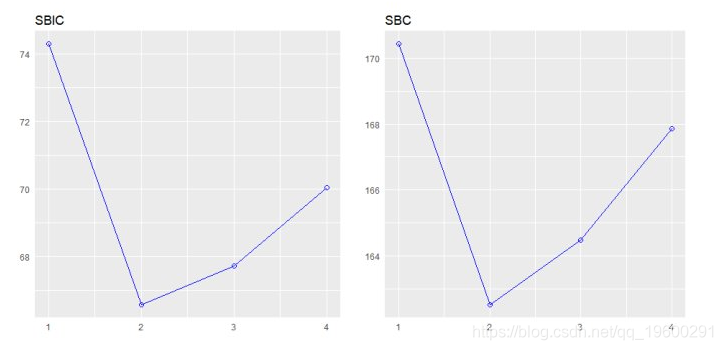
逐步前进回归
从一组候选预测变量中建立回归模型,方法是逐步输入基于p值的预测变量,直到没有变量进入变量。该模型应该包括所有的候选预测变量。如果细节设置为TRUE,则显示每个步骤。
变量选择
# stepwise forward regression
model <- lm(y ~ ., data = surgical)
ols_step_forward(model)
## We are selecting variables based on p value...
## 1 variable(s) added....
## 1 variable(s) added...
## 1 variable(s) added...
## 1 variable(s) added...
## 1 variable(s) added...
## No more variables satisfy the condition of penter: 0.3
## Forward Selection Method
##
## Candidate Terms:
##
## 1 . bcs
## 2 . pindex
## 3 . enzyme_test
## 4 . liver_test
## 5 . age
## 6 . gender
## 7 . alc_mod
## 8 . alc_heavy
##
## ------------------------------------------------------------------------------
## Selection Summary
## ------------------------------------------------------------------------------
## Variable Adj.
## Step Entered R-Square R-Square C(p) AIC RMSE
## ------------------------------------------------------------------------------
## 1 liver_test 0.4545 0.4440 62.5119 771.8753 296.2992
## 2 alc_heavy 0.5667 0.5498 41.3681 761.4394 266.6484
## 3 enzyme_test 0.6590 0.6385 24.3379 750.5089 238.9145
## 4 pindex 0.7501 0.7297 7.5373 735.7146 206.5835
## 5 bcs 0.7809 0.7581 3.1925 730.6204 195.4544
## ------------------------------------------------------------------------------
model <- lm(y ~ ., data = surgical)
k <- ols_step_forward(model)
## We are selecting variables based on p value...
## 1 variable(s) added....
## 1 variable(s) added...
## 1 variable(s) added...
## 1 variable(s) added...
## 1 variable(s) added...
## No more variables satisfy the condition of penter: 0.3
plot(k)