参数检验受制于数据属性的假设。例如，学生t检验是众所周知的参数检验，假设样本均值具有正态分布。由于中心极限定理，如果样本量足够，测试也可以应用于非正态分布的测量。在这里，我们将研究t检验有效所需的大致样本数。
将正态分布拟合到采样均值
为了研究满足学生t检验要求所需的样本数量，我们迭代各种样本量。对于每个样本大小，我们从几个分布中抽取样本。然后，计算样本的平均值，并将正态分布拟合到平均值的分布。在每次迭代中，我们记录描述正态分布与采样均值拟合程度的对数似然。当对数似然变为正时，我们将考虑采样均值接近正态分布。
记录拟合的概率
调查结果，我们可以看到一些分布似乎比其他分布更快地接近正态分布：
<span style="color:#000000"><span style="color:#000000"><code>print(result)</code></span></span>
## Sample_Size Beta Normal Chi Poisson Student
## 1 5 694.9139 -299.81161 -496.33474 -702.94076 -1971.203
## 2 10 823.0384 -126.68806 -297.08253 -515.18702 -3806.447
## 3 15 909.4417 -30.63266 -199.77525 -455.64737 -2119.944
## 4 20 1045.1414 46.45709 -136.21868 -375.75690 -2263.025
## 5 50 1235.7655 278.66189 84.44694 -117.56140 -3427.721
## 6 100 1397.7265 443.81523 281.68706 47.87537 -2178.871
## 7 1000 1996.2198 1019.70692 845.26837 619.25871 -3636.674
## 8 5000 2398.4267 1402.41433 1260.47873 1018.24454 -3231.983根据正对数似然，β分布产生的正态分布均值已经为5的样本大小。正态分布，卡方分布和泊松分布在样本大小分别为20,50和100时产生正态分布均值。最后，学生分布的方式永远不会正常，因为具有一个自由度的分布具有无限的峰度（非常重的尾部），使得中心极限定理不成立。
验证对数似然标准
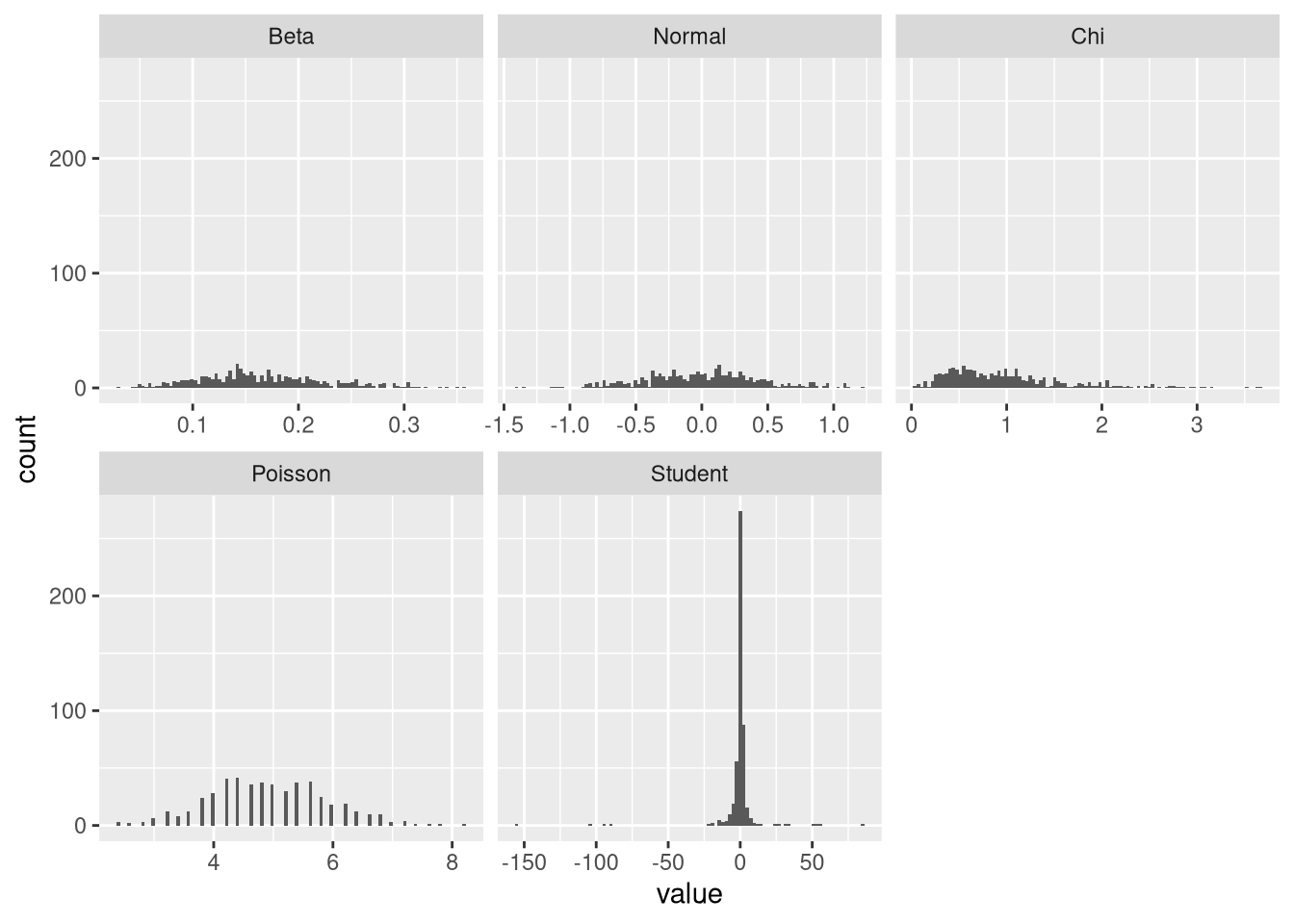
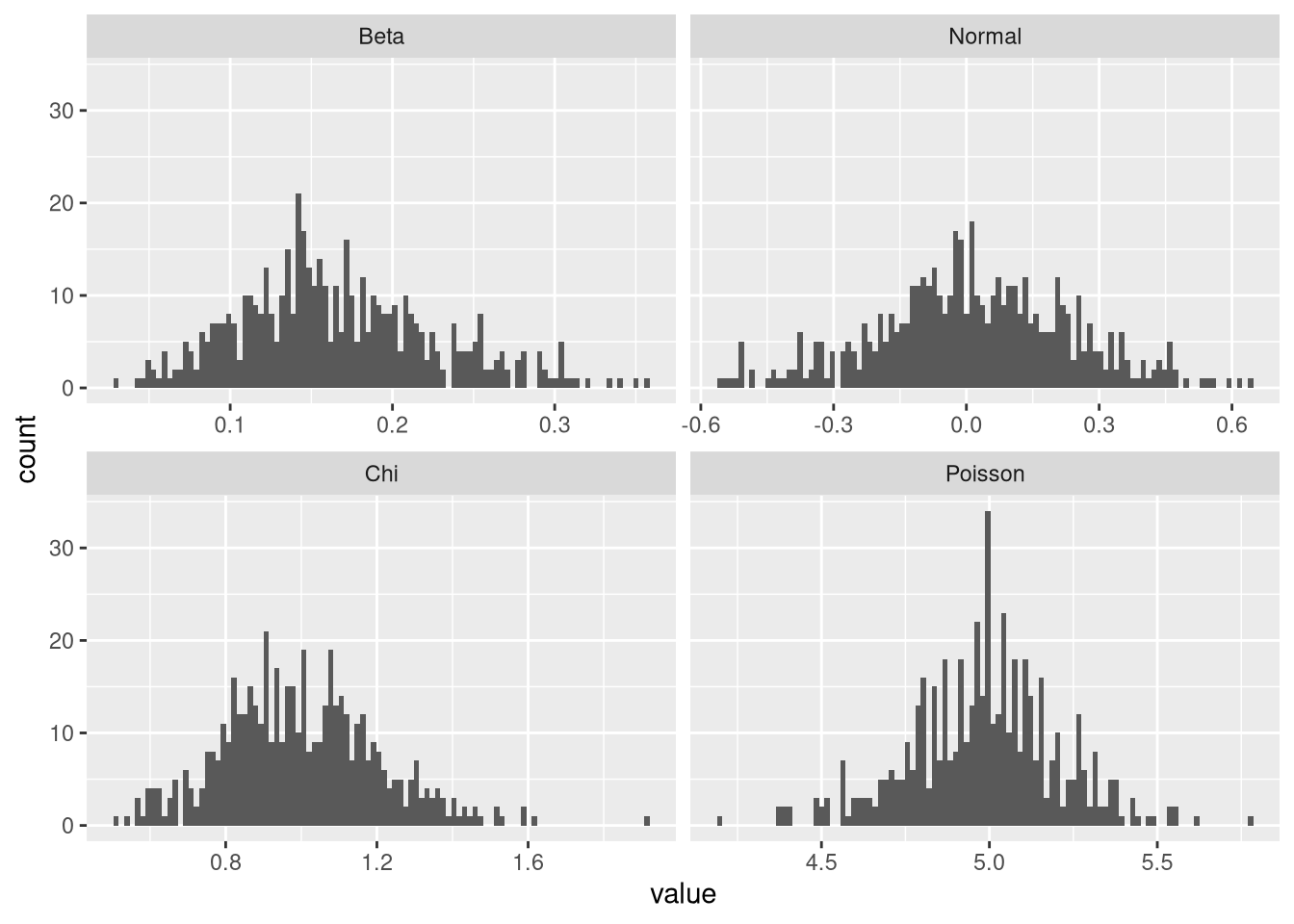
作为结果的验证，让我们绘制样本大小为5的直方图和平均分布变为正常的样本大小：
<span style="color:#000000"><span style="color:#000000"><code>plot.means(norm.means)</code></span></span>
这些结果表明对数似然准则是正态性的充分代理。但请注意，从目视检查来看，平均值的初始贝塔分布似乎不比正态分布更正常。所以这个结果可能是用一粒盐。看看学生的t分布，我们可以看出为什么它的手段不是正态分布的：
<span style="color:#000000"><span style="color:#000000"><code>round(quantile(means$Student), <span style="color:#880000">2</span>)</code></span></span>## 0% 25% 50% 75% 100%
## -495.61 -0.95 0.00 0.98 3422.66对于一些样本，平均分布在分布的两个尾部具有极端异常值。
结论
这些实验的结果表明，对于小于20的样本，绝对应该避免学生t检验。当样本量至少为100时，大多数分布似乎都满足了测试的假设。
总之，特别建议检查样本大小低于100的测量分布。由于中心极限定理不适用于具有无穷方差的分布，因此验证大样本大小的测量分布也是合理的。排除这种分配的可能性。正如我们在这里看到的，即使在5000的样本大小下，根据具有一个自由度的t分布分布的测量也不满足测试的假设。