原文链接:http://tecdat.cn/?p=4051
Double-no-touch(DNT)选项是二元期权,在到期时支付固定金额的现金。我们将展示两种不同的方式来定价包含两种不同定价方法的DNT。
首先,我们将尝试使用正常参数,看看收敛速度有多快:
另一个问题是,如果我们选择极高的ü或极低的L,则会出现计算错误,然而,类似于波动性的问题。如果我们将ü更高或更低,则DNT的价格应该增加。
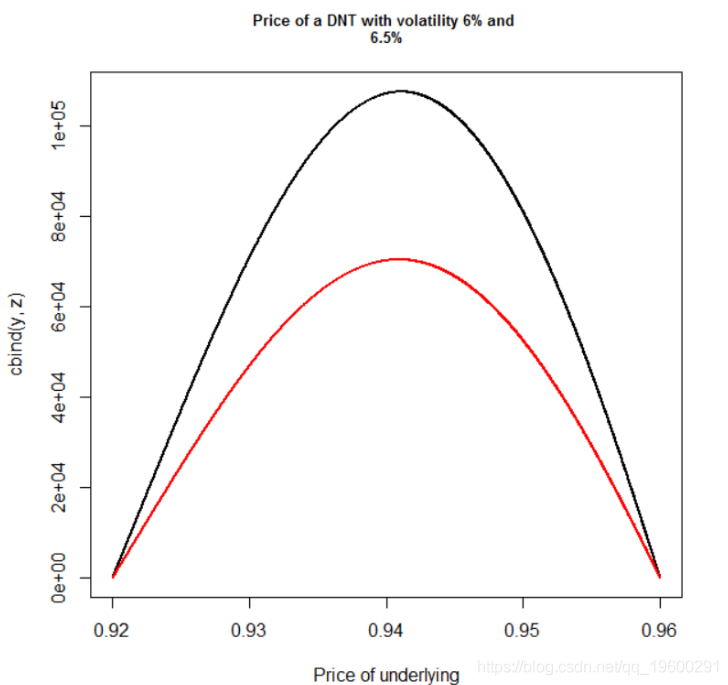
以下代码绘制了底层价格的图表:
以下输出是上述代码的结果:
可以清楚地看到,即使波动率的微小变化也会对DNT的价格产生巨大影响。
大多数最终用户认为最大的风险是现场接近触发点。这是因为最终用户真的以二进制方式考虑二元期权。
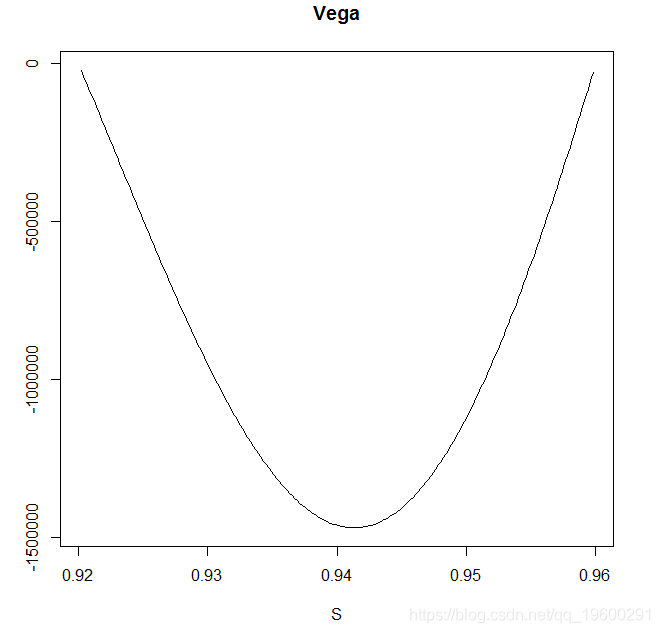
我们可以使用GetGreeks函数来估计维加,γ,δ和有峰。
对于γ,我们可以通过以下方式使用GetGreeks函数:
以下图表是上述代码的结果:
在看了价值图表之后,DNT的增量也非常接近直觉; 如果我们接近更高的障碍,我们的增量变为负值,如果我们接近较低的障碍,增量变为正值如下:
对于动态套期保值者来说,这意味着在价格上涨后买入一些澳元兑美元,并在价格下跌后卖出相同的金额。
可以通过如下的伽玛来描述增量的变化:
负伽玛意味着如果该点上升,我们的增量正在减少,但如果该点下降,我们的增量增加。
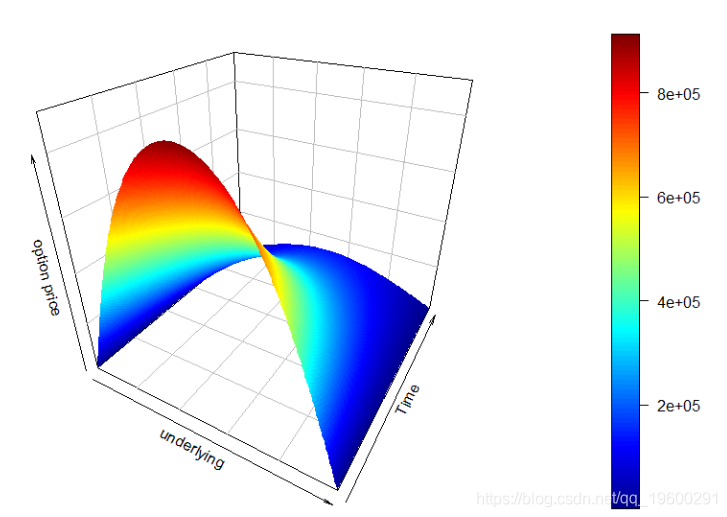
我们之前已经介绍了布莱克 - 斯科尔斯表面; 现在,我们可以详细介绍一下。代码如下:
Double-no-touch 模拟
DNT价格在2014年第二季度的变化情况如何?
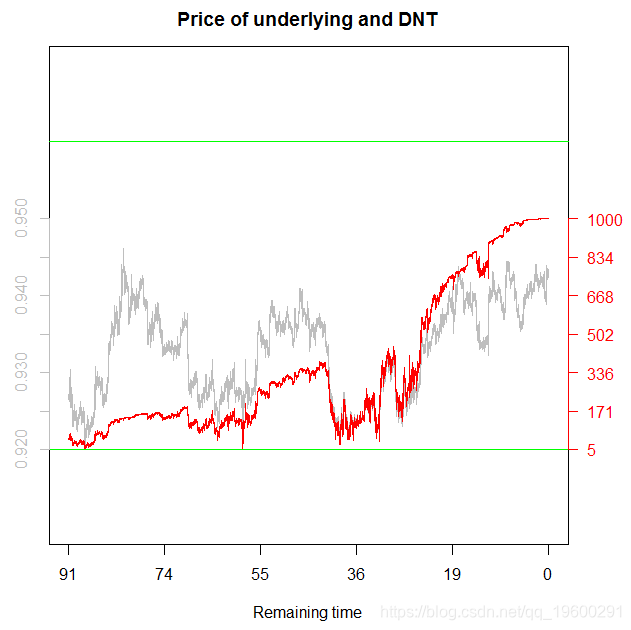
以下是上述代码的输出:
DNT的价格在右轴显示为红色(除以1000),实际的AUDUSD价格在左轴显示为灰色。
比较此5302美元至最初的48564美元期权价格
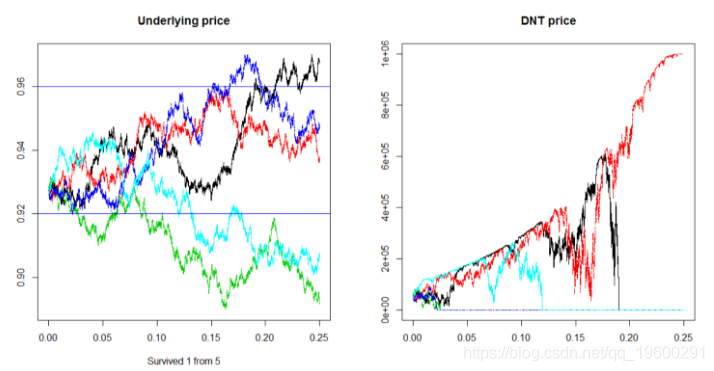
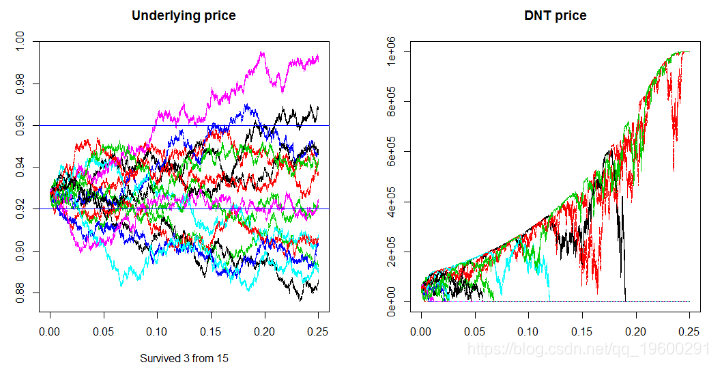
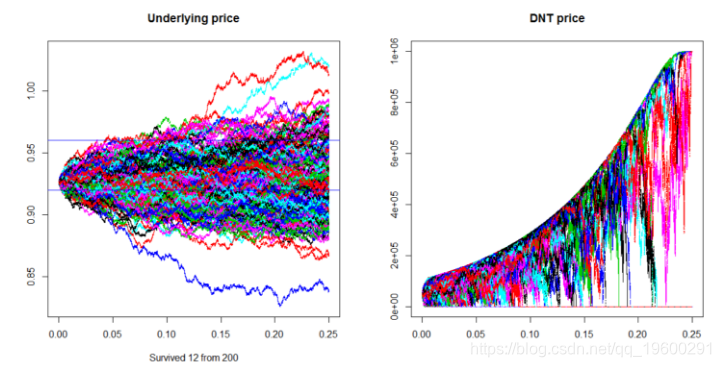
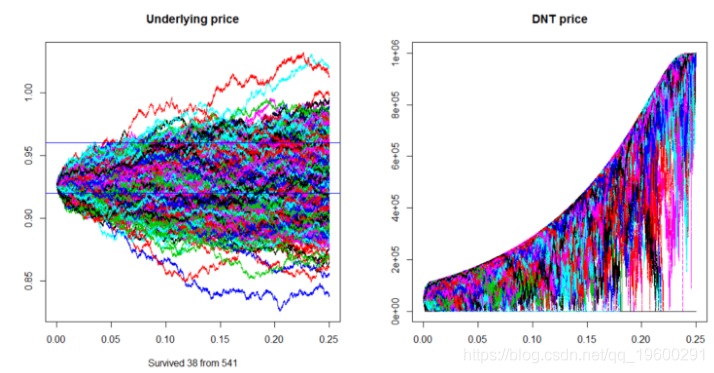
在下面的模拟中,我们将展示一些不同的轨迹所有这些都是从与4月1日黎明时相同的0.9266澳元兑美元现货价格开始,我们将看到其中有多少人保持在(0.9200。0.9600)区间内,为简单起见,我们将使用与我们用于定价DNT相同的6%波动率来模拟几何布朗运动:
以下是上述代码的输出:
如果您有任何疑问,请在下面发表评论。