POJ 1363 Rails（栈）

题目代号：POJ 1363

题目链接：http://poj.org/problem?id=1363

题目原题：

Rails

Time Limit: 1000MS		Memory Limit: 10000K
Total Submissions: 34585		Accepted: 13434

Description

There is a famous railway station in PopPush City. Country there is incredibly hilly. The station was built in last century. Unfortunately, funds were extremely limited that time. It was possible to establish only a surface track. Moreover, it turned out that the station could be only a dead-end one (see picture) and due to lack of available space it could have only one track. 

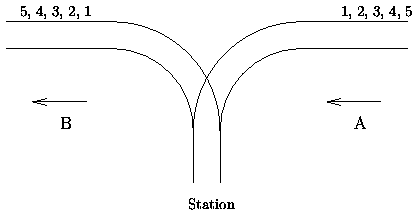
The local tradition is that every train arriving from the direction A continues in the direction B with coaches reorganized in some way. Assume that the train arriving from the direction A has N <= 1000 coaches numbered in increasing order 1, 2, ..., N. The chief for train reorganizations must know whether it is possible to marshal coaches continuing in the direction B so that their order will be a1, a2, ..., aN. Help him and write a program that decides whether it is possible to get the required order of coaches. You can assume that single coaches can be disconnected from the train before they enter the station and that they can move themselves until they are on the track in the direction B. You can also suppose that at any time there can be located as many coaches as necessary in the station. But once a coach has entered the station it cannot return to the track in the direction A and also once it has left the station in the direction B it cannot return back to the station. 

Input

The input consists of blocks of lines. Each block except the last describes one train and possibly more requirements for its reorganization. In the first line of the block there is the integer N described above. In each of the next lines of the block there is a permutation of 1, 2, ..., N. The last line of the block contains just 0. 

The last block consists of just one line containing 0.

Output

The output contains the lines corresponding to the lines with permutations in the input. A line of the output contains Yes if it is possible to marshal the coaches in the order required on the corresponding line of the input. Otherwise it contains No. In addition, there is one empty line after the lines corresponding to one block of the input. There is no line in the output corresponding to the last ``null'' block of the input.

Sample Input

5
1 2 3 4 5
5 4 1 2 3
0
6
6 5 4 3 2 1
0
0

Sample Output

Yes
No

Yes

通过代码：

# include <stdio.h>
# include <string.h>
# include <stdlib.h>
# include <iostream>
# include <fstream>
# include <vector>
# include <queue>
# include <stack>
# include <map>
# include <math.h>
# include <algorithm>
using namespace std;
# define pi acos(-1.0)
# define mem(a,b) memset(a,b,sizeof(a))
# define FOR(i,a,n) for(int i=a; i<=n; ++i)
# define For(i,n,a) for(int i=n; i>=a; --i)
# define FO(i,a,n) for(int i=a; i<n; ++i)
# define Fo(i,n,a) for(int i=n; i>a ;--i)
typedef long long LL;
typedef unsigned long long ULL;

int a[1005],vect[1005],queu[1005];

int main()
{
    for(int i=1;i<=1000;i++)queu[i]=i;
    int n,s;
    while(cin>>n,n)
    {
        while(cin>>s,s)
        {
        bool flag=true;
        int top=0,pop=1,ans=1;
        a[1]=s;
        for(int i=2;i<=n;i++)
        {
            cin>>a[i];
        }
        while(ans<=n)
        {
            if(pop<=n)
            {
                if(a[ans]>=queu[pop])vect[++top]=queu[pop++];
            }
            if(top)
            {
                if(a[ans]==vect[top])ans++,top--;
                else if(a[ans]<vect[top]){flag=false;break;}
            }
        }
        if(flag)cout<<"Yes"<<endl;
        else cout<<"No"<<endl;
        }
        cout<<endl;
    }
    return 0;
}