决策树模型

一、决策树

  决策树的方法在分类、预测、规则提取等领域有着广泛的应用。决策树是一种树形结构，它的每一个叶节点对应一个分类，非叶节点对应某个属性上的划分，根据样本在属性上的取值将其划分为若干个子集。对于非纯的叶节点，多数类的标号给出到达这个节点样本所属的类。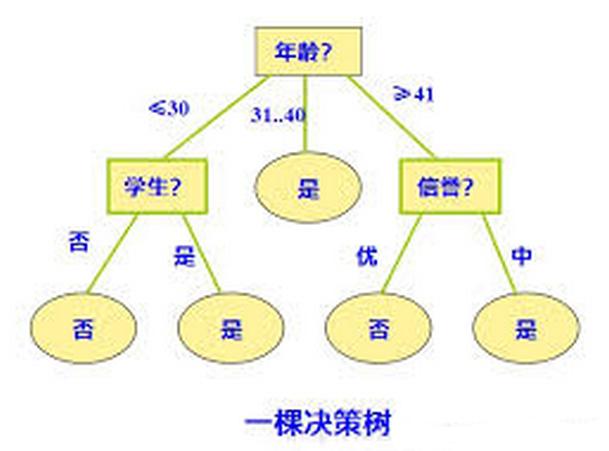

例如上图是一颗决策树，首先它根据年龄分成三颗子树，然后再根据其它属性继续分。决策树的好处是它可以从数据中提取规则，这也符合人的逻辑判断习惯。对于一个数据集，我们可以构造很多棵决策树，决策树算法（ID3、C4.5等）就是根据一定的衡量标准来构造一棵最优的决策树，它使得分类效果最好。这里主要介绍ID3算法的原理和步骤。

二、信息熵介绍

1. 熵与条件熵

  在信息论中，熵是表示随机变量不确定性的度量，设(X)是一个取有限个值的离散随机变量，其概率分布为：

[P(X=x_i)=p_i quad i = 1,2,...,n ]

则随机变量(X)的熵定义为

[H(X)=-p_isum_{i=1}^n{log(p_i)} ]

上式中，通常取对数为以(2)或(e)为低。从上面可知，熵的分布只与(X)的分布有关，而与(X)的取值无关。熵越大，随机变量的不确定性越大，又定义可知

[ 0 leq H(X) leq log(n) ]

一般的，当(n=2)时，(P(X=x_1)=p,P(X=x_2)=1-p),则(X)的熵为

[H(X)=-plog_2(p)-(1-p)log_2(1-p) ]

(H(X))随p的变化图为

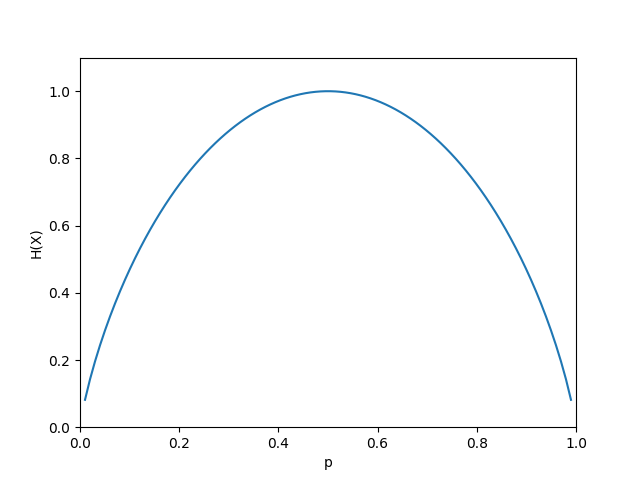
当(p=0)或者(p=1)时，(H(p)=0),随机变量完全没有不确定性，当(p=0.5)时，(H(p)=1),熵取值最大，随机变量不确定性最大。
设有随机变量((X,Y)),其联合概率分布为

[P(X=x_i,Y=y_j)=p_{ij} quad i=1,2,...,n quad j=1,2...m ]

条件熵(H(Y|X))表示已知随机变量(X)的条件下随机变量(Y)的不确定性，即为随机变量(X)给定的条件下随机变量(Y)的条件熵。它的定义为

[H(Y|X)=sum_{i=1}^n{p_iH(Y|X=x_i)} quad quad p_i=P(x=x_i) ]

如果有0概率，则定义(0log0=0)

2.信息增益

  特征(A)对训练数据集(D)的信息增益为(g(D,A)),定义为集合(D)的经验熵(H(D))与特征(A)给定条件下(D)的经验条件熵(H(D|A))之差，即为

[g(D,A)=H(D)-H(D|A) ]

  决策树的学习应用信息增益准则选择特征，给定训练集数据(D)和特征(A),经验熵(H(D))表示对数据集(D)进行分类的不确定性，而经验条件熵(H(D|A))表示在特征(A)给定的条件下对数据集(D)进行分类的不确定性，那么它们的差就表示信息增益。信息增益大的特征具有更强的分类能力。

3. 一个信息增益的计算例子

一个贷款样本的数据表

ID	年龄	有工作	有自己的房子	信贷情况	类别
1	青年	否	否	一般	否
2	青年	否	否	好	否
3	青年	是	否	好	是
4	青年	是	是	一般	是
5	青年	否	否	一般	否
6	中年	否	否	一般	否
7	中年	否	否	好	否
8	中年	是	是	好	是
9	中年	否	是	非常好	是
10	中年	否	是	非常好	是
11	老年	否	是	非常好	是
12	老年	否	是	好	是
13	老年	是	否	好	是
14	老年	是	否	非常好	是
15	老年	否	否	一般	否

下面我们来在计算每个属性条件下的信息增益，然后选择一个信息增益最大的属性。

首先计算训练数据的熵(H(D))

[H(D)=-frac{6}{15}log_2(frac{6}{15})--frac{9}{15}log_2(frac{9}{15})=0.971 ]

然后计算各个特征对(D)的信息增益，从表格左到右特征依次记做(A_1,A_2,A_3,A_4) 则

(1)计算(A_1)条件下信息增益

[g(D,A_1)=H(D)-H(D|A_1)=H(D)-[frac{5}{15}H(D_1)+frac{5}{15}H(D_2)+frac{5}{15}H(D_3)] ]

[=0.971 - frac{5}{15}[-frac{3}{5}log_2(frac{3}{5})-frac{2}{5}log_2(frac{2}{5})] ]

[- frac{5}{15}[-frac{2}{5}log_2(frac{2}{5})-frac{3}{5}log_2(frac{3}{5})] - frac{5}{15}[-frac{1}{5}log_2(frac{1}{5})-frac{4}{5}log_2(frac{4}{5})]=0.083 ]

(2)计算(A_2)条件下信息增益

[g(D,A_2)=H(D)-H(D|A_2)=H(D)-[frac{5}{15}H(D_1)+frac{10}{15}H(D_2)] ]

[=0.971 - frac{5}{15} imes 0-frac{10}{15}[-frac{4}{10}log_2(frac{4}{10})-frac{6}{10}log_2(frac{6}{10})] = 0.324 ]

(3)同理计算(A_3)条件下信息增益

[g(D,A_3)=0.420 ]

(4)同理计算(A_4)条件下信息增益

[g(D,A_4)=0.363 ]

根据比较可知，特征(A_3)条件下信息增益最大，所以最优划分特征为(A_3)

三、ID3算法原理

  ID3算法的思想是在决策树各个节点上应用信息增益准则来选择特征，递归的构建决策树。从根节点开始，对节点计算所有可能的特征的信息增益，选择信息增益最大的特征作为节点特征，由该特征的不同取值建立子节点，再对子节点递归的调用以上方法，构建决策树。算法流程如下：

输入：训练数据(D)，特征(A),阈值 (varepsilon)

输出：决策树(T)

1. 若(D)中所有实例都属于同一类(C_k)，则(T)为单节点树，并将类(C_k)作为该节点的标记，返回(T).
2. 若(A=emptyset),则(T)为单节点树，并将(D)中实例数最大的类(C_k)作为节点的标记，返回(T).
3. 否则计算(A)中各种特征(D)的信息增益，选择信息增益最大的特征(A_g)
4. 如果(A_g)的信息增益小于阈值(varepsilon)，则(T)为单节点树，并将(D)中实例数最大的类(C_k)做为该节点的标记，返回(T)
5. 否则，对(A_g)的每一可能值(a_i),依(A_g=a_i)将(D)分割为若干非空子集(D_i),将(D)i)中实例数最大的类作为标记，构建子节点，由节点及子节点构成树(T),返回(T)
6. 对第i个子结点，以(D_i)为训练集，以(A-{A_g})为特征集，递归调用1 - 5步骤得到子树(T_i),返回(T_i)

（算法用C++实现，待续。。。）

决策树存在的问题

  决策树生成算法递归的生成决策树，直到不能继续下去为止，这样产生的树往往对训练数据的分类很正确，但是对未知测试数据的分类却每那么准确，即出现过拟合现象，过拟合原因在于学习时过多的考率如何提高对训练数据的正确分类，从而构建过于复杂的决策树，解决这类问题常用的做法就是剪枝，对已生成的决策树进行简化。

（就到这里了，以后再完善。。。）