现在给出一个Web统计信息,他们存储着每小时的访问次数。每一行包含连续的小时和信息,以及该小时Web的访问次数。现在要解决的问题是,估计在何时访问量达到基础设施的极限。极限数据是每小时100000次访问。
1.读取数据:
# 获取数据 filepath = r'C:UsersTDDesktopdataMachine Learning1400OS_01_Codesdataweb_traffic.tsv' data = sp.genfromtxt(filepath,delimiter = ' ') x = data[:,0] y = data[:,1]
其中,x表示小时,y表示访问量。
2.预处理和清洗数据:
print sp.sum(sp.isnan(y))
结果显示含有8个控值,为了方便,在此处理缺失值办法是直接剔除。
x = x[~sp.isnan(y)] y = y[~sp.isnan(y)]
接下来,画出散点图,观察数据的规律:
# 可视化,观察数据规律
plt.scatter(x,y)
plt.title('Web traffic over the last month')
plt.xlabel('Time')
plt.ylabel('Hits/hours')
plt.xticks([w*24*7 for w in range(5)],
['week {}'.format(i) for i in range(5)])
plt.autoscale(tight = True)
plt.grid()
plt.show()
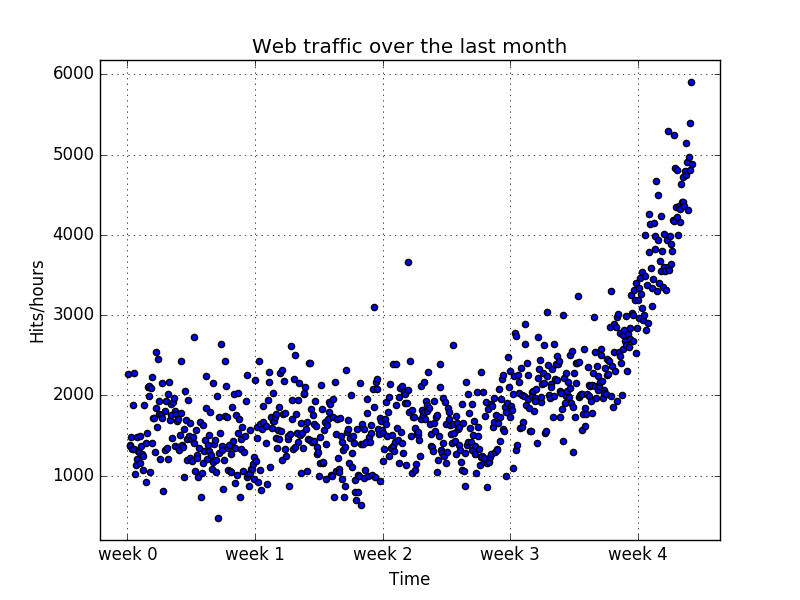
3 选择正确的模型和学习算法:
回答原始问题需要明确以下几点:
1)找到噪声数据后真正的模型
2)使用这个模型预测未来,一遍解决我们的问题
1.首先需要明白模型与实际数据区别。模型可以理解为对复杂现实世界简化的理论近似。它总会包含一些劣质的类容,这个就叫做近似误差。我们用真实数据与模型预测的数据之间的平方距离来计算这个误差,对于一个训练好的模型f,按照下面函数来计算误差:
def error(f,x,y): return sp.sum((f(x)-y)**2)
2.简单的线性模型
现在用一个线性模型来拟合上面数据,看看可以得到什么。
plt.scatter(x,y)
plt.title('Web traffic over the last month')
plt.xlabel('Time')
plt.ylabel('Hits/hours')
plt.xticks([w*24*7 for w in range(5)],
['week {}'.format(i) for i in range(5)])
plt.autoscale(tight = True)
plt.grid()
# 开始构建模型,使用1阶多项式拟合
p1 = sp.polyfit(x,y,1)
f1 = sp.poly1d(p1) # 将拟合系数传入ployld函数创建模型函数f1
fx = sp.linspace(0,x[-1],1000)
plt.plot(fx,f1(fx),linewidth = 3)
plt.legend(["d = {}".format(f1.order)], loc = "upper left")
plt.show()
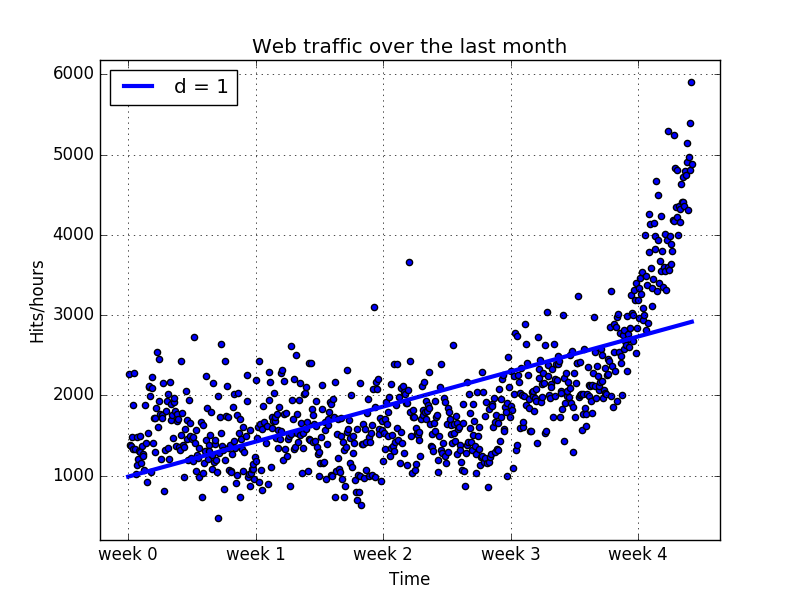
上图显示了第一个训练的模型,发现前四个星期好像没有偏差很多,可以清楚的看到直线模型的假设是有问题的。
3 接下来用3阶,10阶,50阶多项式来拟合:
colors = ['g', 'k', 'b', 'm', 'r']
def error(f,x,y):
return sp.sum((f(x)-y)**2)
def plot_models(x, y, models, fname, mx = None):
plt.clf()
plt.scatter(x, y, s=10)
plt.title("Web traffic over the last month")
plt.xlabel("Time")
plt.ylabel("Hits/hour")
plt.xticks(
[w * 7 * 24 for w in range(10)], ['week %i' % w for w in range(10)])
if models:
if mx is None:
mx = sp.linspace(0, x[-1], 1000)
for model, color in zip(models, colors):
# print "Model:",model
# print "Coeffs:",model.coeffs
plt.plot(mx, model(mx), c = color,linewidth = 1.5)
plt.legend(["d = {}".format(m.order) for m in models], loc="upper left")
plt.autoscale(tight=True)
plt.grid(True, linestyle='-', color='0.75')
plt.savefig(fname)
# create and plot models
os.chdir(r'C:UsersTDDesktopdataMachine Learning1400OS_01_Codesdata')
f1 = sp.poly1d(sp.polyfit(x,y,1))
f3 = sp.poly1d(sp.polyfit(x, y, 3))
f10 = sp.poly1d(sp.polyfit(x, y, 10))
f50 = sp.poly1d(sp.polyfit(x, y, 50))
plot_models(
x, y, [f1,f3, f10, f50],"2.png")
# error
indices = [1,3,10,50]
for index,model in zip(indices,[f1,f3,f10,f50]):
print 'Error d= {} : {}'.format(index,error(model,x,y))
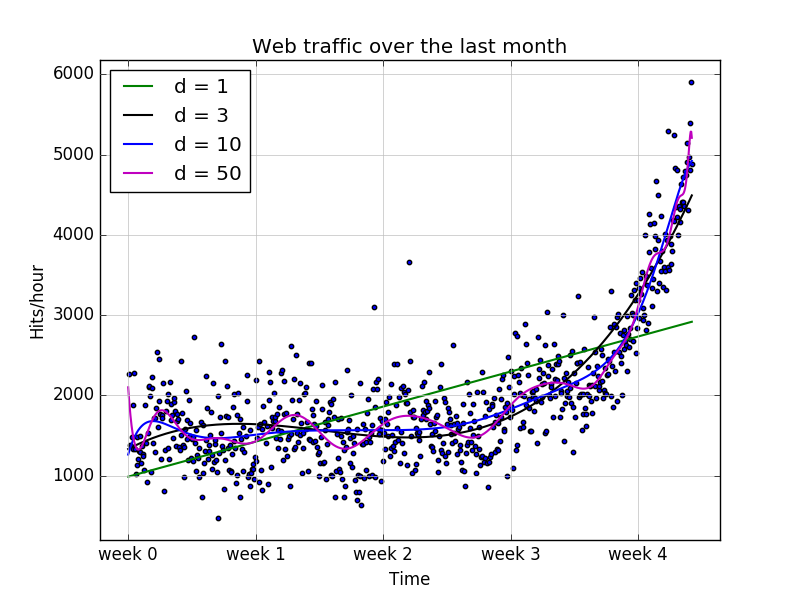
可以看出多项式越复杂,数据逼近越好。他们误差如下:
Error d= 1 : 317389767.34
Error d= 3 : 139350144.032
Error d= 10 : 121942326.364
Error d= 50 : 109504607.366
看看10阶和100阶的多项式,我们发现了巨大的震荡。似乎这样拟合的太过了,他不断捕捉到背后数据的生成,还把噪声数据也考虑进去了。这样叫做过拟合。然而1阶的显然太简单了,不能反映数据的规律,这种叫做欠拟合。不管是欠拟合还是过拟合,都不适合进行预测。
4 已退为进,另眼看数据
观察数据,似乎第三周和第四周之间有一个拐点。这可以让我们将3.5周作为分界点,把数据分为两份,并训练出两条直线。
plt.scatter(x, y, s=10)
plt.title("Web traffic over the last month")
plt.xlabel("Time")
plt.ylabel("Hits/hour")
plt.xticks(
[w * 7 * 24 for w in range(10)], ['week %i' % w for w in range(10)])
inflection = int(3.5*7*24)
xa = x[:inflection]
ya = y[:inflection]
xb = x[inflection:]
yb = y[inflection:]
fa = sp.poly1d(sp.polyfit(xa,ya,1))
fb = sp.poly1d(sp.polyfit(xb,yb,1))
plt.scatter(x,y)
fax = sp.linspace(0,x[-1],1000)
fbx = sp.linspace(x[inflection]/1.1,x[-1]*1.1,1000)
plt.plot(fax,fa(fax),c = 'g',linewidth = 2.5)
plt.plot(fbx,fb(fbx),c = 'r',linewidth = 2.5)
plt.show()
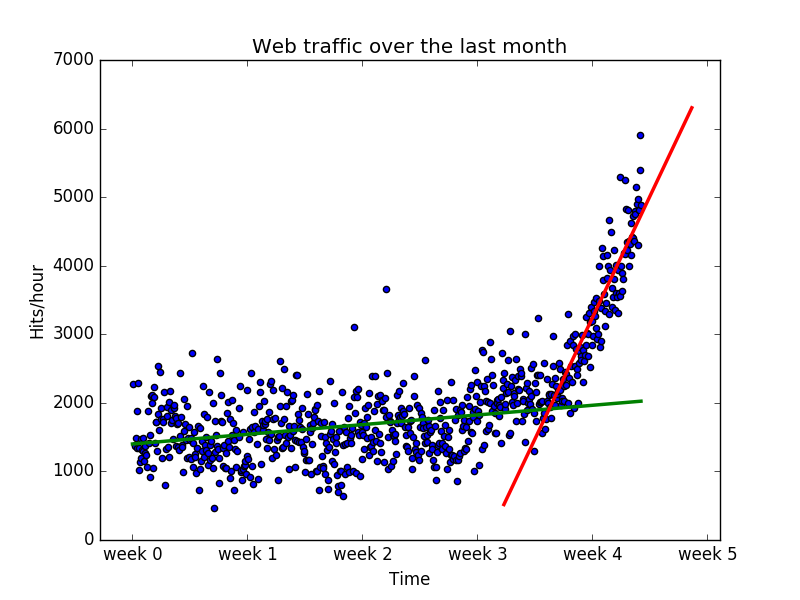
很明显,这两条直线组合起来似乎比之前任何模型都可以更好的拟合数据,虽然组合后的误差高于高阶多项式的误差。为什么仅仅在最后一周上更相信线性模型呢?这是因为我们认为他更好的符合未来数据。10阶和100阶多项式在此没有光明的未来,他们只是非常努力的对给定的数据进行拟合,但是他们却无法推广到将来的数据上,这就是过拟合,另外低阶模型也不能恰好的模拟数据,叫做欠拟合。
5 训练与测试
如果有些外来数据用于模型评估,那么仅从近似误差结果就可以判断出我们的选择的模型是好还是坏。尽管我们找不到未来数据,但是可以从现有的数据中拿出一部分,来判断我们的结果是好还是坏了。利用拐点后的数据进行训练,得到的二阶模型的误差最小,这个模型很适中,既不欠拟合也不过拟合。
6 回答最初的问题
得到了训练的模型。只需要带入数值就可以计算得到我们所求结果。
实验代码:
#!/usr/bin/env python
# -*- coding: utf-8 -*-
# __author__ : '小糖果'
import scipy as sp
import matplotlib.pyplot as plt
from scipy.optimize import fsolve
import os
# 获取数据
filepath = r'C:UsersTDDesktopdataMachine Learning1400OS_01_Codesdata'
data = sp.genfromtxt(os.path.join(filepath,'web_traffic.tsv'),delimiter = ' ')
x = data[:,0]
y = data[:,1]
# 缺失数据处理,用相邻数据平均数代替
print sp.sum(sp.isnan(y))
x = x[~sp.isnan(y)]
y = y[~sp.isnan(y)]
colors = ['g', 'k', 'b', 'm', 'r']
def error(f,x,y):
return sp.sum((f(x)-y)**2)
def plot_model(x, y,models = None,fname = None,mx = None):
plt.clf()
plt.scatter(x,y)
plt.title("Web traffic over the last month")
plt.xlabel("Time")
plt.ylabel("Hits/hour")
plt.xticks([w*24*7 for w in range(10)],
['week {}'.format(i) for i in range(10)])
if models:
if mx is None:
mx = sp.linspace(0,x[-1],1000)
for (model,color) in zip(models,colors):
plt.plot(mx,model(mx),c = color,linewidth = 2)
plt.legend(['d = {}'.format(m.order) for m in models],loc = 'upper left')
plt.autoscale(tight = True)
plt.grid(True)
if fname:
plt.savefig(fname)
else:
plt.show()
# 查看初始数据
plot_model(x,y,fname = os.path.join(filepath,'1.jpg'))
#分别用1,2,10,50阶多项式拟合
f1 = sp.poly1d(sp.polyfit(x,y,1))
f2 = sp.poly1d(sp.polyfit(x,y,2))
f10 = sp.poly1d(sp.polyfit(x,y,10))
f50 = sp.poly1d(sp.polyfit(x,y,50))
plot_model(x,y,models = [f1,f2,f10,f50],fname = os.path.join(filepath,'2.jpg'))
# 线性分段拟合
plt.clf()
inflection = int(3.5*7*24)
xa = x[:inflection]
ya = y[:inflection]
xb = x[inflection:]
yb = y[inflection:]
fa = sp.poly1d(sp.polyfit(xa,ya,1))
fb = sp.poly1d(sp.polyfit(xb,yb,1))
plt.scatter(x,y)
fax = sp.linspace(0,x[-1],1000)
fbx = sp.linspace(x[inflection]/1.1,x[-1]*1.1,1000)
plt.plot(fax,fa(fax),c = 'g',linewidth = 2.5)
plt.plot(fbx,fb(fbx),c = 'r',linewidth = 2.5)
plt.grid(True)
plt.savefig(os.path.join(filepath,'3.jpg'))
# 只使用后面部分数据
f1 = sp.poly1d(sp.polyfit(xb,yb,1))
f2 = sp.poly1d(sp.polyfit(xb,yb,2))
f10 = sp.poly1d(sp.polyfit(xb,yb,10))
f50 = sp.poly1d(sp.polyfit(xb,yb,50))
plot_model(xb,yb,models = [f1,f2,f10,f50],
mx = sp.linspace(xb[0],xb[-1],100),
fname = os.path.join(filepath,'4,jpg'))
# 求问题的解,使用二次多项式模型
ans = fsolve(f2 - 100000,800)/7/24
print ans