CF19E Fairy

题目链接

题意分析

一个图是二分图的充要条件：该图中不存在奇环

由于奇偶性的关系 复杂奇环的产生一定源于简单奇环 所以我们仅仅考虑删去一条边使得所有简单奇环被破坏

也就说 我们仅仅考虑简单环

首先 我们从这张图中拽出一个生成树

然后 对于非树边 如果加上去的话 必然会产生一个环 我们需要统计会产生奇环的数量cnt

如果cnt=0

那么一开始就不再奇环 而我们删边是不可能删出奇环的 所以这种情况下m条边都可以删

如果cnt≠0

树边

对于每一条树边 如果参与构成奇数环的话 就是a类型边 否则就是b类型边

显然我们对于树边就是要讨论a类型边中哪些边删了会使得奇环全部消失

第一反应 很显然 如果一条树边参与形成了全部奇环的话 是必须要删除的

但是 会存在这么一种情况

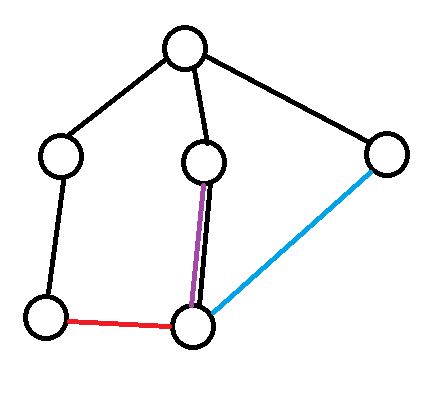
其中黑色的是树边 显然 我们应该删除紫边 但是紫边不仅参与形成了奇环 还参与形成了偶环 由于奇偶性 删除了紫边 还会有一个大奇环

所以我们要删除的是参与形成奇环并且没有参与形成偶环的树边

这个的话 利用树上差分赋值边权的方法可以办到

对于奇数环上的树边边权+1 对于偶数环上的树边边权-1

最后边权=cnt的树边就是我们要删除的树边

非树边

如果存在多个奇环的话 只删掉一条非树边显然只能消去一个奇环 不可行

如果只存在一个奇环的话 只删掉一条非树边显然是可行的

一定要注意的是 题目给出的图可能不是连通图

CODE:

#include<bits/stdc++.h>
using namespace std;
#define M 10080
int n,m,tot,cnt;
int bel[M];
vector<pair<int,int> > G[M];
int dep[M],fa[M][20],siz[M],id[M];
int sum[M],ans[M];
bool vis[M];
struct Edge
{
	int u,v;
	bool tag;
}e[M];
int find(int x)
{return x==bel[x] ? x:bel[x]=find(bel[x]);}
void add(int x,int y,int z)
{G[x].push_back(make_pair(y,z));}
void dfs(int now,int fat)
{
	dep[now]=dep[fat]+1;fa[now][0]=fat;
	for(int i=1;(1<<i)<=dep[now];++i)
	fa[now][i]=fa[fa[now][i-1]][i-1];
	for(int i=0;i<(int)G[now].size();++i)
	{
		int v=G[now][i].first;
		if(v==fat) continue;
		id[v]=G[now][i].second;dfs(v,now);
	}
}
int LCA(int nowx,int nowy)
{
	if(dep[nowx]<dep[nowy]) swap(nowx,nowy);
	for(int i=16;i>=0;--i)
	if(dep[fa[nowx][i]]>=dep[nowy]) nowx=fa[nowx][i];
	if(nowx==nowy) return nowx;
	for(int i=16;i>=0;--i)
	if(fa[nowx][i]!=fa[nowy][i]) 
	nowx=fa[nowx][i],nowy=fa[nowy][i];
	return fa[nowx][0];
}
void dfs_sum(int now,int fat)
{
	vis[now]=1;
	for(int i=0;i<(int)G[now].size();++i)
	{
		int v=G[now][i].first;
		if(v==fat) continue;
		dfs_sum(v,now);
		sum[now]+=sum[v];
	}
}
int main()
{
	scanf("%d%d",&n,&m);
	for(int i=1;i<=m;++i)
	{
		scanf("%d%d",&e[i].u,&e[i].v);
		e[i].tag=0;
	} 
	for(int i=1;i<=n;++i) bel[i]=i;
	for(int i=1;i<=m;++i)
	{
		int fx=find(e[i].u),fy=find(e[i].v);
		if(fx==fy) continue;
		bel[fx]=fy;e[i].tag=1;
		add(e[i].u,e[i].v,i);add(e[i].v,e[i].u,i); 	
	} 
	for(int i=1;i<=n;++i) if(!dep[i]) dfs(i,0);
	tot=0;
	for(int i=1;i<=m;++i)
	{
		if(e[i].tag) continue;
		int lca=LCA(e[i].u,e[i].v);
		int tmpnum=dep[e[i].u]+dep[e[i].v]-(dep[lca]<<1);
		if((tmpnum+1)&1)//是奇环的话
		{
			sum[e[i].u]++;sum[e[i].v]++;
			sum[lca]-=2;
			++tot;
		} 
		else//是偶环的话 
		{
			sum[e[i].u]--;sum[e[i].v]--;
			sum[lca]+=2;
		}
	}
	for(int i=1;i<=n;++i) if(!vis[i]) dfs_sum(i,0);
	if(tot==0)
	{
		printf("%d\n",m);
		for(int i=1;i<=m;++i) printf("%d%c",i,(i==m ? '\n':' ')); 
	}
	if(tot==1)
	{
		for(int i=1;i<=m;++i)
		{
			if(e[i].tag) continue;
			int lca=LCA(e[i].u,e[i].v);
			int tmpnum=dep[e[i].u]+dep[e[i].v]-(dep[lca]<<1);
			if((tmpnum+1)&1) ans[++cnt]=i;
		}	
		for(int i=1;i<=n;++i)
		if(sum[i]==1) ans[++cnt]=id[i];
		sort(ans+1,ans+cnt+1);
		printf("%d\n",cnt);
		for(int i=1;i<=cnt;++i) printf("%d%c",ans[i],(i==cnt ? '\n':' ')); 
	}
	if(tot>1)
	{
		
		for(int i=1;i<=n;++i)
		if(sum[i]==tot) ans[++cnt]=id[i];
		sort(ans+1,ans+cnt+1);
		printf("%d\n",cnt);
		for(int i=1;i<=cnt;++i) printf("%d%c",ans[i],(i==cnt ? '\n':' ')); 
	}
	return 0;
}