1.堆基础
二叉堆的定义:
1.二叉堆是一个完全二叉树结构。完全二叉树不一定是一个满二叉树。完全二叉树左节点必须是满的,右节点为可以为空。把元素一层一层的从左往右依次排列。
2.当满足该节点的左右孩子节点都小于该节点时,称为最大堆。反之,当该节点的左右孩子节点大于该节点时,称为最小堆。

2.手动实现最大堆及复杂度分析

package com.tc.javabase.datastructure.tree.heap;
import com.tc.javabase.datastructure.array.ArrayList;
public class MaxHeap<E extends Comparable<E>> {
private ArrayList<E> data;
public MaxHeap(int capacity){
data = new ArrayList<>(capacity);
}
public MaxHeap(){
data = new ArrayList<>();
}
public MaxHeap(E[] arr){
data = new ArrayList<>(arr);
if(arr.length != 1){
for(int i = parent(arr.length - 1) ; i >= 0 ; i --)
siftDown(i);
}
}
// 返回堆中的元素个数
public int size(){
return data.getSize();
}
// 返回一个布尔值, 表示堆中是否为空
public boolean isEmpty(){
return data.isEmpty();
}
// 返回完全二叉树的数组表示中,一个索引所表示的元素的父亲节点的索引
private int parent(int index){
if(index == 0)
throw new IllegalArgumentException("index-0 doesn't have parent.");
return (index - 1) / 2;
}
// 返回完全二叉树的数组表示中,一个索引所表示的元素的左孩子节点的索引
private int leftChild(int index){
return index * 2 + 1;
}
// 返回完全二叉树的数组表示中,一个索引所表示的元素的右孩子节点的索引
private int rightChild(int index){
return index * 2 + 2;
}
// 向堆中添加元素
public void add(E e){
data.addLast(e);
siftUp(data.getSize() - 1);
}
private void siftUp(int k){
while(k > 0 && data.get(parent(k)).compareTo(data.get(k)) < 0 ){
data.swap(k, parent(k));
k = parent(k);
}
}
// 看堆中的最大元素
public E findMax(){
if(data.getSize() == 0)
throw new IllegalArgumentException("Can not findMax when heap is empty.");
return data.get(0);
}
// 取出堆中最大元素
public E extractMax(){
E ret = findMax();
data.swap(0, data.getSize() - 1);
data.removeLast();
siftDown(0);
return ret;
}
private void siftDown(int k){
while(leftChild(k) < data.getSize()){
int j = leftChild(k); // 在此轮循环中,data[k]和data[j]交换位置
if( j + 1 < data.getSize() &&
data.get(j + 1).compareTo(data.get(j)) > 0 )
j ++;
// data[j] 是 leftChild 和 rightChild 中的最大值
if(data.get(k).compareTo(data.get(j)) >= 0 )
break;
data.swap(k, j);
k = j;
}
}
// 取出堆中的最大元素,并且替换成元素e
public E replace(E e){
E ret = findMax();
data.set(0, e);
siftDown(0);
return ret;
}
}
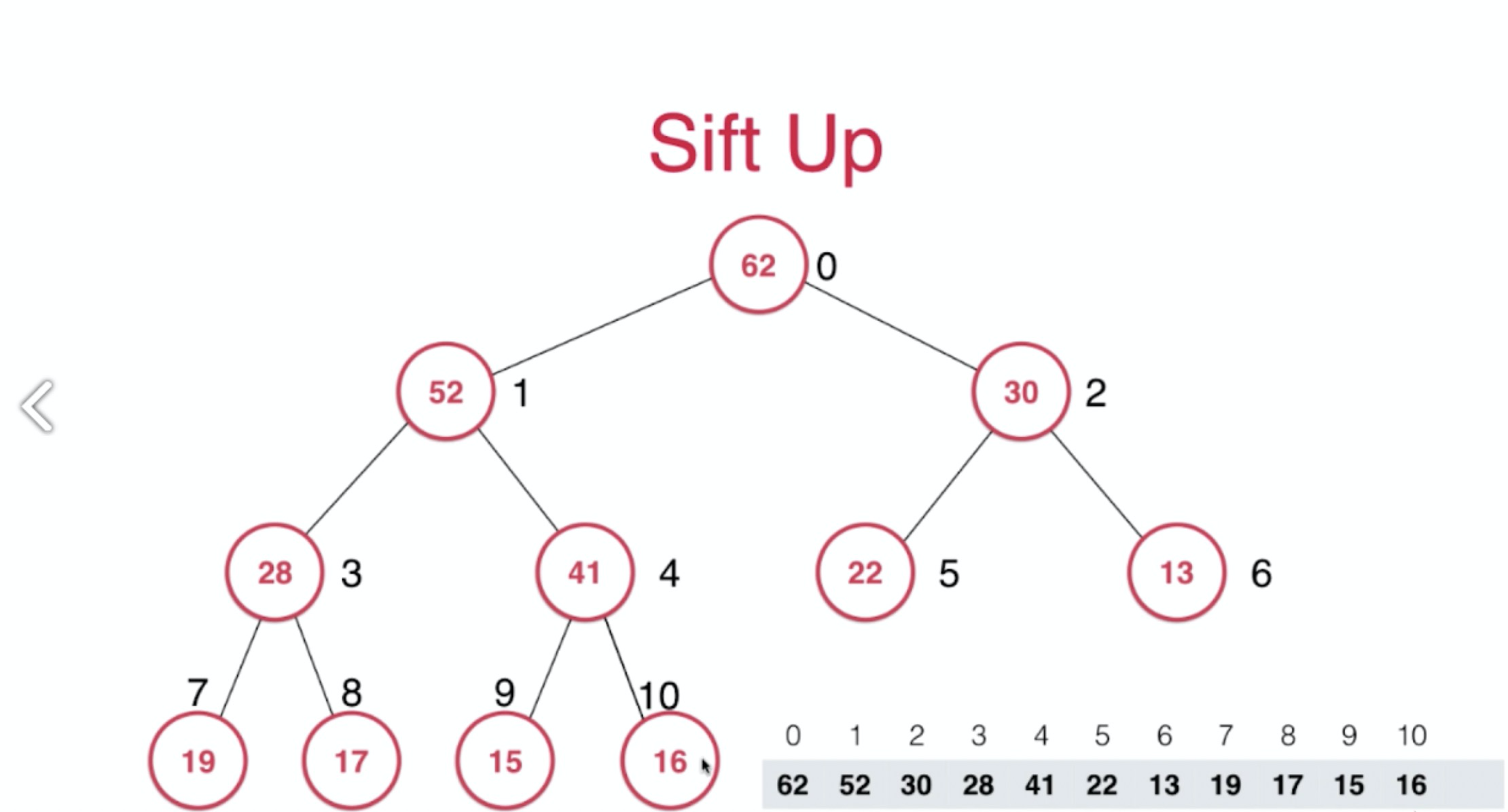
Sift Up(上浮):当我们往堆中添加了个元素的时候,在堆的最后添加一个元素,再将该元素进行上浮操作,即和它的父节点一直进行比较,若比它的父节点大则交换位置,否则不动。
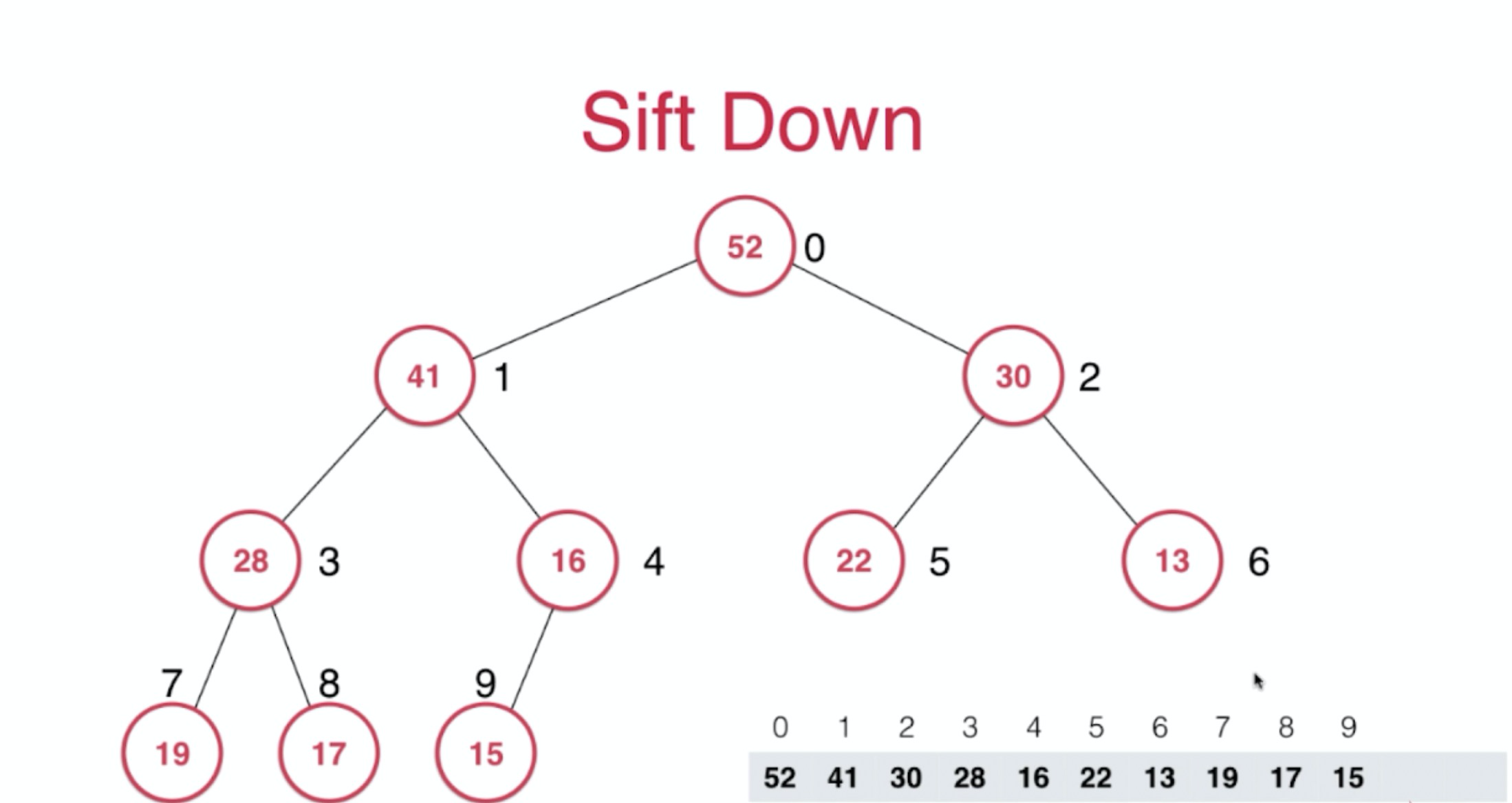
Sift Down(下沉):当我们取出堆中最大的元素时,首先将根元素和最尾端的元素进行交换位置,然后删掉最尾端的元素,然后再将此时的顶端元素进行下层操作,即将该元素和它的左右孩子中的最大的一个进行比较,若比它小则交换位置否则不动 。
问题:考虑给你一个没有顺序的数组,然后用给排成一个二叉最大堆的结构
若直接将该数组扫描一遍,然后依次进行add操作则时间复杂度为nLog(n),那么有没有更好的方法?
Heapify(堆排序):即将依次从最后一个非叶子节点到根节点依次做Sift Down操作,此时的时间复杂度为O(n)。