一,前言
TreeMap:基于红黑树实现的,TreeMap是有序的。
二,TreeMap结构
2.1 红黑树结构
红黑树又称红-黑二叉树,它首先是一颗二叉树,它具体二叉树所有的特性。同时红黑树更是一颗自平衡的排序二叉树。我们知道一颗基本的二叉树他们都需要满足一个基本性质--即树中的任何节点的值大于它的左子节点,且小于它的右子节点。按照这个基本性质使得树的检索效率大大提高。我们知道在生成二叉树的过程是非常容易失衡的,最坏的情况就是一边倒(只有右/左子树),这样势必会导致二叉树的检索效率大大降低(O(n)),所以为了维持二叉树的平衡,大牛们提出了各种实现的算法,如:AVL,SBT,伸展树,TREAP ,红黑树等等。
平衡二叉树必须具备如下特性:它是一棵空树或它的左右两个子树的高度差的绝对值不超过1,并且左右两个子树都是一棵平衡二叉树。也就是说该二叉树的任何一个等等子节点,其左右子树的高度都相等。
红黑树的特点:
1、每个节点都只能是红色或者黑色
2、根节点是黑色
3、每个叶节点(NIL节点,空节点)是黑色的。
4、如果一个结点是红的,则它两个子节点都是黑的。也就是说在一条路径上不能出现相邻的两个红色结点。
5、从任一节点到其每个叶子的所有路径都包含相同数目的黑色节点。
这些约束强制了红黑树的关键性质: 从根到叶子的最长的可能路径不多于最短的可能路径的两倍长。结果是这棵树大致上是平衡的。因为操作比如插入、删除和查找某个值的最坏情况时间都要求与树的高度成比例,这个在高度上的理论上限允许红黑树在最坏情况下都是高效的,而不同于普通的二叉查找树。所以红黑树它是复杂而高效的,其检索效率O(log n)。下图为一颗典型的红黑二叉树。
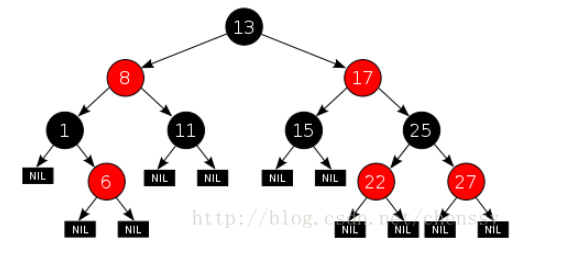
对于红黑树的其他内容可以参照:http://www.cnblogs.com/yangecnu/p/Introduce-Red-Black-Tree.html
2.2 TreeMap红黑树节点
前面已经说个TreeMap是基于红黑树结构实现的。如下是JDK中红黑树节点的代码:
static final class Entry<K,V> implements Map.Entry<K,V> { K key; //键 V value; //值 Entry<K,V> left = null; //左孩子节点 Entry<K,V> right = null; //右孩子节点 Entry<K,V> parent; //父节点 boolean color = BLACK; //节点的颜色,在红黑树种,只有两种颜色,红色和黑色 //构造方法,用指定的key,value ,parent初始化,color默认为黑色 Entry(K key, V value, Entry<K,V> parent) { this.key = key; this.value = value; this.parent = parent; } //返回key public K getKey() { return key; } //返回该节点对应的value public V getValue() { return value; } //替换节点的值,并返回旧值 public V setValue(V value) { V oldValue = this.value; this.value = value; return oldValue; } //重写equals()方法 public boolean equals(Object o) { if (!(o instanceof Map.Entry)) return false; Map.Entry<?,?> e = (Map.Entry<?,?>)o; //两个节点的key相等,value相等,这两个节点才相等 return valEquals(key,e.getKey()) && valEquals(value,e.getValue()); } //重写hashCode()方法 public int hashCode() { int keyHash = (key==null ? 0 : key.hashCode()); int valueHash = (value==null ? 0 : value.hashCode()); //key和vale hash值得异或运算,相同则为零,不同则为1 return keyHash ^ valueHash; } //重写toString()方法 public String toString() { return key + "=" + value; } }
三,TreeMap源码阅读
3.1 TreeMap的继承关系
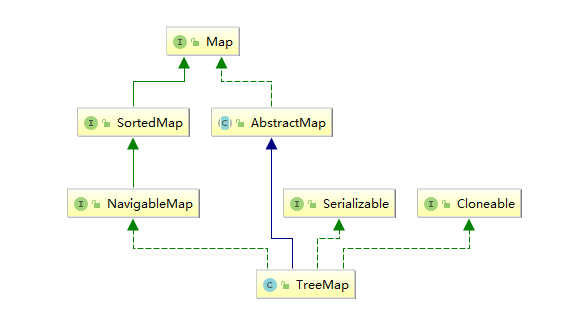
TreeMap实现了SotredMap接口,它是有序的集合。而且是一个红黑树结构,每个key-value都作为一个红黑树的节点。如果在调用TreeMap的构造函数时没有指定比较器,则根据key执行自然排序。
3.2 TreeMap的成员变量
private final Comparator<? super K> comparator; //比较器,是自然排序,还是定制排序 ,使用final修饰,表明一旦赋值便不允许改变 private transient Entry<K,V> root = null; //红黑树的根节点 private transient int size = 0; //TreeMap中存放的键值对的数量 private transient int modCount = 0; //修改的次数
3.3 TreeMap的构造方法
//空参构造方法,comparator用键的顺序做比较 public TreeMap() { comparator = null; } //构造方法,提供比较器,用指定比较器排序 public TreeMap(Comparator<? super K> comparator) { his.comparator = comparator; } //将m中的元素转化daoTreeMap中,按照键的顺序做比较排序 public TreeMap(Map<? extends K, ? extends V> m) { comparator = null; putAll(m); } //构造方法,指定的参数为SortedMap //采用m的比较器排序 public TreeMap(SortedMap<K, ? extends V> m) { comparator = m.comparator(); try { buildFromSorted(m.size(), m.entrySet().iterator(), null, null); } catch (java.io.IOException cannotHappen) { } catch (ClassNotFoundException cannotHappen) { } }
3.4 TreeMap的常用方法
public int size() {} // 返回个数 public boolean containsKey(Object key) {} // 是否包含某个key public boolean containsValue(Object value) {} // 是否包含某个值 public V get(Object key) {} // 根据key取值 public Comparator<? super K> comparator() {} // 排序的算法 public K firstKey() {} // 返回第一个key public K lastKey() {} // 返回最后一个key public void putAll(Map<? extends K, ? extends V> map) {} // 添加多个 public V put(K key, V value) {} // 添加一个 public V remove(Object key) {} // 删除 public void clear() {} // 清空 public Object clone() {} // 复制 public Map.Entry<K,V> firstEntry() {} public Map.Entry<K,V> lastEntry() {} public Map.Entry<K,V> pollFirstEntry() {} public Map.Entry<K,V> pollLastEntry() {} public Map.Entry<K,V> lowerEntry(K key) {} public K lowerKey(K key) {} public Map.Entry<K,V> floorEntry(K key) {} public K floorKey(K key) {} public Map.Entry<K,V> ceilingEntry(K key) {} public K ceilingKey(K key) {} public Map.Entry<K,V> higherEntry(K key) {} public K higherKey(K key) {} public Set<K> keySet() {} public NavigableSet<K> navigableKeySet() {} public NavigableSet<K> descendingKeySet() {} public Collection<V> values() {} public Set<Map.Entry<K,V>> entrySet() {} public NavigableMap<K,V> subMap(K fromKey, boolean fromInclusive,K toKey, boolean toInclusive) {} public NavigableMap<K,V> headMap(K toKey, boolean inclusive) {} public NavigableMap<K,V> tailMap(K fromKey, boolean inclusive) {} public SortedMap<K,V> subMap(K fromKey, K toKey) {} public SortedMap<K,V> headMap(K toKey) {} public SortedMap<K,V> tailMap(K fromKey) {} @Override public boolean replace(K key, V oldValue, V newValue) {} // 对应值替换 @Override public V replace(K key, V value) {} // 替换 @Override public void forEach(BiConsumer<? super K, ? super V> action) {} // 提供便利 @Override public void replaceAll(BiFunction<? super K, ? super V, ? extends V> function) {}
四,总结
因为TreeMap是有序的,TreeMap的增删改查和统计相关的操作的时间复杂度都为 O(logn).相对于HashMap和LikedHashMap 这些 hash表的时间复杂度O(1)(不考虑冲突情况),TreeMap的增删改查的时间复杂度为O(logn)就显得效率较低。HashMap并不保证任何顺序性。LikedHashMap额外保证了Map的遍历顺序与put顺序一致的有序性。