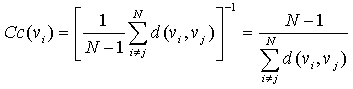7-1 求组合数(15 分)
本题要求编写程序,根据公式C(m,n)=n!/(m!(n-m)!)算出从n个不同元素中取出m个元素(m≤n)的组合数。
建议定义和调用函数fact(n)计算n!,其中n的类型是int,函数类型是double。
输入格式:
输入在一行中给出两个正整数m和n(m≤n),以空格分隔。
输出格式:
按照格式“result = 组合数计算结果”输出。题目保证结果在double类型范围内。
输入样例:
2 7
输出样例:
result = 211 #include<bits/stdc++.h> 2 using namespace std; 3 long long fact(int n) 4 { 5 long long sum=1; 6 for(int i=2;i<=n;i++) 7 sum*=i; 8 return sum; 9 } 10 int main() 11 { 12 int n,m; 13 scanf("%d%d",&m,&n); 14 printf("result = %lld",fact(n)/(fact(m)*fact(n-m))); 15 return 0; 16 }
7-3 判断上三角矩阵(15 分)
上三角矩阵指主对角线以下的元素都为0的矩阵;主对角线为从矩阵的左上角至右下角的连线。
本题要求编写程序,判断一个给定的方阵是否上三角矩阵。
输入格式:
输入第一行给出一个正整数T,为待测矩阵的个数。接下来给出T个矩阵的信息:每个矩阵信息的第一行给出一个不超过10的正整数n。随后n行,每行给出n个整数,其间以空格分隔。
输出格式:
每个矩阵的判断结果占一行。如果输入的矩阵是上三角矩阵,输出“YES”,否则输出“NO”。
输入样例:
2
3
1 2 3
0 4 5
0 0 6
2
1 0
-8 2
输出样例:
YES
NO1 #include<bits/stdc++.h> 2 using namespace std; 3 int main() 4 { 5 int t,a; 6 cin>>t; 7 while(t--) 8 { 9 int n,flag=1; 10 cin>>n; 11 for(int i=0;i<n;i++) 12 for(int j=0;j<n;j++) 13 { 14 cin>>a; 15 if(j<i&&a!=0) 16 flag=0; 17 } 18 printf("%s ",flag==1?"YES":"NO"); 19 } 20 return 0; 21 }
7-4 整数152的各位数字(10 分)
本题要求编写程序,输出整数152的个位数字、十位数字和百位数字的值。
输入格式:
本题无输入。
输出格式:
按照以下格式输出:
152 = 个位数字 + 十位数字*10 + 百位数字*100
1 #include<bits/stdc++.h> 2 using namespace std; 3 int main() 4 { 5 printf("152 = 2 + 5*10 + 1*100"); 6 return 0; 7 }
7-5 韩信点兵(10 分)
在中国数学史上,广泛流传着一个“韩信点兵”的故事:韩信是汉高祖刘邦手下的大将,他英勇善战,智谋超群,为汉朝建立了卓越的功劳。据说韩信的数学水平也非常高超,他在点兵的时候,为了知道有多少兵,同时又能保住军事机密,便让士兵排队报数:
- 按从1至5报数,记下最末一个士兵报的数为1;
- 再按从1至6报数,记下最末一个士兵报的数为5;
- 再按从1至7报数,记下最末一个士兵报的数为4;
- 最后按从1至11报数,最末一个士兵报的数为10;
请编写程序计算韩信至少有多少兵。
输入格式:
本题无输入
输出格式:
输出韩信至少拥有的士兵人数。
#include<bits/stdc++.h> using namespace std; int main() { for(int i=1;;i++) { if(i%5==1&&i%6==5&&i%7==4&&i%11==10) { printf("%d",i); break; } } return 0; }
7-6 表格输出(5 分)
本题要求编写程序,按照规定格式输出表格。
输入格式:
本题目没有输入。
输出格式:
------------------------------------
Province Area(km2) Pop.(10K)
------------------------------------
Anhui 139600.00 6461.00
Beijing 16410.54 1180.70
Chongqing 82400.00 3144.23
Shanghai 6340.50 1360.26
Zhejiang 101800.00 4894.00
------------------------------------1 #include<bits/stdc++.h> 2 using namespace std; 3 int main() 4 { 5 cout<<"------------------------------------ " 6 <<"Province Area(km2) Pop.(10K) " 7 <<"------------------------------------ " 8 <<"Anhui 139600.00 6461.00 " 9 <<"Beijing 16410.54 1180.70 " 10 <<"Chongqing 82400.00 3144.23 " 11 <<"Shanghai 6340.50 1360.26 " 12 <<"Zhejiang 101800.00 4894.00 " 13 <<"------------------------------------ "; 14 return 0; 15 }
7-7 混合类型数据格式化输入(5 分)
本题要求编写程序,顺序读入浮点数1、整数、字符、浮点数2,再按照字符、整数、浮点数1、浮点数2的顺序输出。
输入格式:
输入在一行中顺序给出浮点数1、整数、字符、浮点数2,其间以1个空格分隔。
输出格式:
在一行中按照字符、整数、浮点数1、浮点数2的顺序输出,其中浮点数保留小数点后2位。
输入样例:
2.12 88 c 4.7
输出样例:
c 88 2.12 4.701 #include<bits/stdc++.h> 2 using namespace std; 3 int main() 4 { 5 double a,b; 6 int c; 7 char ch; 8 scanf("%lf %d %c %lf",&a,&c,&ch,&b); 9 printf("%c %d %.2f %.2f",ch,c,a,b); 10 return 0; 11 }
7-2 水仙花数(20 分)
水仙花数是指一个N位正整数(N≥3),它的每个位上的数字的N次幂之和等于它本身。例如:153=13+53+33。 本题要求编写程序,计算所有N位水仙花数。
输入格式:
输入在一行中给出一个正整数N(3≤N≤7)。
输出格式:
按递增顺序输出所有N位水仙花数,每个数字占一行。
输入样例:
3
输出样例:
153
370
371
4071 #include<bits/stdc++.h> 2 using namespace std; 3 int Pow(int a,int n) 4 { 5 int sum=a; 6 for(int i=1;i<n;i++) 7 sum*=a; 8 return sum; 9 } 10 int main() 11 { 12 int n; 13 cin>>n; 14 int a=Pow(10,n-1),b=Pow(10,n); 15 for(int i=a;i<b;i++) 16 { 17 int sum=0,div=1; 18 for(int j=0;j<n;j++) 19 sum+=Pow(i/div%10,n),div*=10; 20 if(sum==i) 21 printf("%d ",i); 22 } 23 return 0; 24 }
7-10 整除光棍(20 分)
这里所谓的“光棍”,并不是指单身汪啦~ 说的是全部由1组成的数字,比如1、11、111、1111等。传说任何一个光棍都能被一个不以5结尾的奇数整除。比如,111111就可以被13整除。 现在,你的程序要读入一个整数x,这个整数一定是奇数并且不以5结尾。然后,经过计算,输出两个数字:第一个数字s,表示x乘以s是一个光棍,第二个数字n是这个光棍的位数。这样的解当然不是唯一的,题目要求你输出最小的解。
提示:一个显然的办法是逐渐增加光棍的位数,直到可以整除x为止。但难点在于,s可能是个非常大的数 —— 比如,程序输入31,那么就输出3584229390681和15,因为31乘以3584229390681的结果是111111111111111,一共15个1。
输入格式:
输入在一行中给出一个不以5结尾的正奇数x(<1000)。
输出格式:
在一行中输出相应的最小的s和n,其间以1个空格分隔。
输入样例:
31
输出样例:
3584229390681 15模拟下大数除以小数,now/x为商
1 #include<bits/stdc++.h> 2 using namespace std; 3 int main() 4 { 5 int x,p=0,now=0,Len=0; 6 scanf("%d",&x); 7 while(++Len) 8 { 9 now=now*10+1; 10 if(p||now/x) 11 cout<<now/x,p=1; 12 now%=x; 13 if(now==0) 14 { 15 cout<<' '<<Len; 16 break; 17 } 18 } 19 return 0; 20 }
7-8 银行业务队列简单模拟(25 分)
设某银行有A、B两个业务窗口,且处理业务的速度不一样,其中A窗口处理速度是B窗口的2倍 —— 即当A窗口每处理完2个顾客时,B窗口处理完1个顾客。给定到达银行的顾客序列,请按业务完成的顺序输出顾客序列。假定不考虑顾客先后到达的时间间隔,并且当不同窗口同时处理完2个顾客时,A窗口顾客优先输出。
输入格式:
输入为一行正整数,其中第1个数字N(≤1000)为顾客总数,后面跟着N位顾客的编号。编号为奇数的顾客需要到A窗口办理业务,为偶数的顾客则去B窗口。数字间以空格分隔。
输出格式:
按业务处理完成的顺序输出顾客的编号。数字间以空格分隔,但最后一个编号后不能有多余的空格。
输入样例:
8 2 1 3 9 4 11 13 15
输出样例:
1 3 2 9 11 4 13 15
1 #include<bits/stdc++.h> 2 using namespace std; 3 vector<int> A,B,C; 4 int main() 5 { 6 int n,t,a; 7 cin>>n; 8 for(int i=0;i<n;i++) 9 { 10 cin>>a; 11 if(a%2)A.push_back(a); 12 else B.push_back(a); 13 } 14 int la=A.size(),lb=B.size(); 15 int aa=0,bb=0; 16 for(int i=0;i<la+lb;i++) 17 { 18 if(aa<la)C.push_back(A[aa++]); 19 if(aa<la)C.push_back(A[aa++]); 20 if(bb<lb)C.push_back(B[bb++]); 21 } 22 for(int i=0;i<C.size();i++) 23 if(i==0)cout<<C[i]; 24 else cout<<' '<<C[i]; 25 return 0; 26 }
7-9 修理牧场(25 分)
农夫要修理牧场的一段栅栏,他测量了栅栏,发现需要N块木头,每块木头长度为整数Li个长度单位,于是他购买了一条很长的、能锯成N块的木头,即该木头的长度是Li的总和。
但是农夫自己没有锯子,请人锯木的酬金跟这段木头的长度成正比。为简单起见,不妨就设酬金等于所锯木头的长度。例如,要将长度为20的木头锯成长度为8、7和5的三段,第一次锯木头花费20,将木头锯成12和8;第二次锯木头花费12,将长度为12的木头锯成7和5,总花费为32。如果第一次将木头锯成15和5,则第二次锯木头花费15,总花费为35(大于32)。
请编写程序帮助农夫计算将木头锯成N块的最少花费。
输入格式:
输入首先给出正整数N(N≤104),表示要将木头锯成N块。第二行给出N个正整数(N≤50),表示每段木块的长度。输入样例:
8
4 5 1 2 1 3 1 1
输出样例:
49每次取出优先队列前两个最小的组成1个
1 #include<bits/stdc++.h> 2 using namespace std; 3 int main() 4 { 5 priority_queue<int,vector<int>,greater<int> > Q; 6 int n; 7 long long int a,b; 8 cin>>n; 9 for(int i=0;i<n;i++) 10 { 11 cin>>a; 12 Q.push(a); 13 } 14 int sum=0; 15 while(Q.size()>1) 16 { 17 a=Q.top();Q.pop(); 18 b=Q.top();Q.pop(); 19 sum+=a+b; 20 Q.push(a+b); 21 } 22 printf("%d ",sum); 23 return 0; 24 }
7-13 QQ帐户的申请与登陆(25 分)
实现QQ新帐户申请和老帐户登陆的简化版功能。最大挑战是:据说现在的QQ号码已经有10位数了。
输入格式:
输入首先给出一个正整数N(≤105),随后给出N行指令。每行指令的格式为:“命令符(空格)QQ号码(空格)密码”。其中命令符为“N”(代表New)时表示要新申请一个QQ号,后面是新帐户的号码和密码;命令符为“L”(代表Login)时表示是老帐户登陆,后面是登陆信息。QQ号码为一个不超过10位、但大于1000(据说QQ老总的号码是1001)的整数。密码为不小于6位、不超过16位、且不包含空格的字符串。
输出格式:
针对每条指令,给出相应的信息:
1)若新申请帐户成功,则输出“New: OK”;
2)若新申请的号码已经存在,则输出“ERROR: Exist”;
3)若老帐户登陆成功,则输出“Login: OK”;
4)若老帐户QQ号码不存在,则输出“ERROR: Not Exist”;
5)若老帐户密码错误,则输出“ERROR: Wrong PW”。
输入样例:
5
L 1234567890 myQQ@qq.com
N 1234567890 myQQ@qq.com
N 1234567890 myQQ@qq.com
L 1234567890 myQQ@qq
L 1234567890 myQQ@qq.com
输出样例:
ERROR: Not Exist
New: OK
ERROR: Exist
ERROR: Wrong PW
Login: OK1 #include<bits/stdc++.h> 2 using namespace std; 3 int main() 4 { 5 int n,hm; 6 char zl[5],mm[20]; 7 scanf("%d",&n); 8 map<int,string> ma; 9 for(int i=0;i<n;i++) 10 { 11 scanf("%s %d %s",zl,&hm,mm); 12 if(zl[0]=='L') 13 { 14 if(ma.find(hm)!=ma.end()) 15 if(ma[hm]==mm)//3 16 printf("Login: OK "); 17 else//5 18 printf("ERROR: Wrong PW "); 19 else//4 20 printf("ERROR: Not Exist "); 21 } 22 if(zl[0]=='N') 23 { 24 if(ma.find(hm)==ma.end())//1 25 { 26 ma[hm]=mm; 27 printf("New: OK "); 28 } 29 else//2 30 printf("ERROR: Exist "); 31 } 32 } 33 return 0; 34 }
7-12 约瑟夫环(25 分)
N个人围成一圈顺序编号,从1号开始按1、2、3......顺序报数,报p者退出圈外,其余的人再从1、2、3开始报数,报p的人再退出圈外,以此类推。 请按退出顺序输出每个退出人的原序号。
输入格式:
输入只有一行,包括一个整数N(1<=N<=3000)及一个整数p。
输出格式:
按退出顺序输出每个退出人的原序号,数据间以一个空格分隔,但行尾无空格。
输入样例:
在这里给出一组输入。例如:
7 3
输出样例:
3 6 2 7 5 1 4
1 #include<bits/stdc++.h> 2 using namespace std; 3 vector<int> v; 4 int a[3005]; 5 int main() 6 { 7 int n,p,b=0,cnt=0,i=1; 8 cin>>n>>p; 9 while(1) 10 { 11 if(!a[i]) 12 { 13 if(++b==p) 14 { 15 v.push_back(i); 16 b=0;a[i]=1; 17 if(++cnt==n)break; 18 } 19 } 20 if(++i>n)i=1; 21 } 22 for(int i=0;i<v.size();i++) 23 printf("%d%c",v[i],i==v.size()-1?' ':' '); 24 return 0; 25 }
7-13 家谱处理(30 分)
人类学研究对于家族很感兴趣,于是研究人员搜集了一些家族的家谱进行研究。实验中,使用计算机处理家谱。为了实现这个目的,研究人员将家谱转换为文本文件。下面为家谱文本文件的实例:
John
Robert
Frank
Andrew
Nancy
David
家谱文本文件中,每一行包含一个人的名字。第一行中的名字是这个家族最早的祖先。家谱仅包含最早祖先的后代,而他们的丈夫或妻子不出现在家谱中。每个人的子女比父母多缩进2个空格。以上述家谱文本文件为例,John这个家族最早的祖先,他有两个子女Robert和Nancy,Robert有两个子女Frank和Andrew,Nancy只有一个子女David。
在实验中,研究人员还收集了家庭文件,并提取了家谱中有关两个人关系的陈述语句。下面为家谱中关系的陈述语句实例:
John is the parent of Robert
Robert is a sibling of Nancy
David is a descendant of Robert
研究人员需要判断每个陈述语句是真还是假,请编写程序帮助研究人员判断。
输入格式:
输入首先给出2个正整数N(2≤N≤100)和M(≤100),其中N为家谱中名字的数量,M为家谱中陈述语句的数量,输入的每行不超过70个字符。
名字的字符串由不超过10个英文字母组成。在家谱中的第一行给出的名字前没有缩进空格。家谱中的其他名字至少缩进2个空格,即他们是家谱中最早祖先(第一行给出的名字)的后代,且如果家谱中一个名字前缩进k个空格,则下一行中名字至多缩进k+2个空格。
在一个家谱中同样的名字不会出现两次,且家谱中没有出现的名字不会出现在陈述语句中。每句陈述语句格式如下,其中X和Y为家谱中的不同名字:
X is a child of Y
X is the parent of Y
X is a sibling of Y
X is a descendant of Y
X is an ancestor of Y
输出格式:
对于测试用例中的每句陈述语句,在一行中输出True,如果陈述为真,或False,如果陈述为假。
输入样例:
6 5
John
Robert
Frank
Andrew
Nancy
David
Robert is a child of John
Robert is an ancestor of Andrew
Robert is a sibling of Nancy
Nancy is the parent of Frank
John is a descendant of Andrew
输出样例:
True
True
True
False
False
1 #include<bits/stdc++.h> 2 using namespace std; 3 int main() 4 { 5 int n,m,k; 6 string s,F[105];//存父亲 7 map<string,string> fa;//映射父亲 8 cin>>n>>m;cin.get(); 9 for(int i=0;i<n;i++) 10 { 11 getline(cin,s); 12 k=count(s.begin(),s.end(),' '); 13 s=s.substr(k); 14 if(k==0) 15 { 16 fa[s]="NULL";//祖宗自己没有父亲 17 F[k]=s;//0个空格自己做为父亲F[0],给2个空格的儿子用的 18 } 19 else 20 { 21 fa[s]=F[k/2-1];//2个空格父亲为F[0],4个空格父亲为F[1],以此类推 22 F[k/2]=s;//2个空格自己做为父亲F[1],给4个空格的儿子用的 23 } 24 } 25 for(int i=0;i<m;i++) 26 { 27 int f=0; 28 string X,Y,P,a; 29 cin>>X>>a>>a>>P>>a>>Y; 30 if(P=="child")//X的父亲是Y 31 if(fa[X]==Y) 32 f=1; 33 if(P=="parent")//Y的父亲是X 34 if(fa[Y]==X) 35 f=1; 36 if(P=="sibling") 37 if(fa[X]==fa[Y])//X和Y父亲相同(兄弟) 38 f=1; 39 if(P=="descendant")//X的祖宗是Y 40 { 41 while(fa[X]!=Y&&fa[X]!="NULL")X=fa[X];//向上找Y,若找到或者遇到NULL则结束 42 if(fa[X]==Y)f=1; 43 } 44 if(P=="ancestor")//Y的祖宗是X 45 { 46 while(fa[Y]!=X&&fa[Y]!="NULL")Y=fa[Y];//向上找X,若找到或者遇到NULL则结束 47 if(fa[Y]==X)f=1; 48 } 49 printf("%s ",f?"True":"False"); 50 } 51 return 0; 52 }
7-14 社交网络图中结点的“重要性”计算(30 分)
在社交网络中,个人或单位(结点)之间通过某些关系(边)联系起来。他们受到这些关系的影响,这种影响可以理解为网络中相互连接的结点之间蔓延的一种相互作用,可以增强也可以减弱。而结点根据其所处的位置不同,其在网络中体现的重要性也不尽相同。
“紧密度中心性”是用来衡量一个结点到达其它结点的“快慢”的指标,即一个有较高中心性的结点比有较低中心性的结点能够更快地(平均意义下)到达网络中的其它结点,因而在该网络的传播过程中有更重要的价值。在有N个结点的网络中,结点vi的“紧密度中心性”Cc(vi)数学上定义为vi到其余所有结点vj (j≠i) 的最短距离d(vi,vj)的平均值的倒数:
对于非连通图,所有结点的紧密度中心性都是0。
给定一个无权的无向图以及其中的一组结点,计算这组结点中每个结点的紧密度中心性。
输入格式:
输入第一行给出两个正整数N和M,其中N(N≤104)是图中结点个数,顺便假设结点从1到N编号;M(M≤105)是边的条数。随后的M行中,每行给出一条边的信息,即该边连接的两个结点编号,中间用空格分隔。最后一行给出需要计算紧密度中心性的这组结点的个数K(K≤100)以及K个结点编号,用空格分隔。输出格式:
按照Cc(i)=x.xx的格式输出K个给定结点的紧密度中心性,每个输出占一行,结果保留到小数点后2位。
输入样例:
9 14
1 2
1 3
1 4
2 3
3 4
4 5
4 6
5 6
5 7
5 8
6 7
6 8
7 8
7 9
3 3 4 9
输出样例:
Cc(3)=0.47
Cc(4)=0.62
Cc(9)=0.35这个题可以floyd过的(不知道为啥??10000ˆ3),这里用spfa,如果有1个点不能到Dist[i]=无穷直接返回0
1 #include<bits/stdc++.h> 2 using namespace std; 3 typedef pair<int,int> pii; 4 const int N=10005,INF=0x3f3f3f3f; 5 vector<pii> G[N]; 6 int Vis[N],Dist[N]; 7 int spfa(int s,int n) 8 { 9 memset(Vis,0,sizeof(Vis)); 10 memset(Dist,INF,sizeof(Dist)); 11 queue<int> Q; 12 Q.push(s); 13 Dist[s]=0; 14 while(!Q.empty()) 15 { 16 int u=Q.front();Q.pop(); 17 Vis[u]=0; 18 for(int i=0;i<G[u].size();i++) 19 { 20 int v=G[u][i].first; 21 int w=G[u][i].second; 22 if(Dist[v]>Dist[u]+w) 23 { 24 Dist[v]=Dist[u]+w; 25 if(!Vis[v]) 26 { 27 Q.push(v); 28 Vis[v]=1; 29 } 30 } 31 } 32 } 33 int sum=0; 34 for(int i=1;i<=n;i++) 35 if(Dist[i]==INF)return 0; 36 else sum+=Dist[i]; 37 return sum; 38 } 39 int main() 40 { 41 int n,m,u,v,k; 42 scanf("%d%d",&n,&m); 43 for(int i=0;i<m;i++) 44 { 45 scanf("%d%d",&u,&v); 46 G[u].push_back(pii(v,1)); 47 G[v].push_back(pii(u,1)); 48 } 49 scanf("%d",&k); 50 for(int i=0;i<k;i++) 51 { 52 scanf("%d",&u); 53 int sum=spfa(u,n); 54 printf("Cc(%d)=%.2f ",u,sum==0?0.00:(n-1)*1.0/sum); 55 } 56 return 0; 57 }
7-15 周游世界(30 分)
周游世界是件浪漫事,但规划旅行路线就不一定了…… 全世界有成千上万条航线、铁路线、大巴线,令人眼花缭乱。所以旅行社会选择部分运输公司组成联盟,每家公司提供一条线路,然后帮助客户规划由联盟内企业支持的旅行路线。本题就要求你帮旅行社实现一个自动规划路线的程序,使得对任何给定的起点和终点,可以找出最顺畅的路线。所谓“最顺畅”,首先是指中途经停站最少;如果经停站一样多,则取需要换乘线路次数最少的路线。
输入格式:
输入在第一行给出一个正整数N(≤100),即联盟公司的数量。接下来有N行,第i行(i=1,⋯,N)描述了第i家公司所提供的线路。格式为:
M S[1] S[2] ⋯ S[M]
其中M(≤100)是经停站的数量,S[i](i=1,⋯,M)是经停站的编号(由4位0-9的数字组成)。这里假设每条线路都是简单的一条可以双向运行的链路,并且输入保证是按照正确的经停顺序给出的 —— 也就是说,任意一对相邻的S[i]和S[i+1](i=1,⋯,M−1)之间都不存在其他经停站点。我们称相邻站点之间的线路为一个运营区间,每个运营区间只承包给一家公司。环线是有可能存在的,但不会不经停任何中间站点就从出发地回到出发地。当然,不同公司的线路是可能在某些站点有交叉的,这些站点就是客户的换乘点,我们假设任意换乘点涉及的不同公司的线路都不超过5条。
在描述了联盟线路之后,题目将给出一个正整数K(≤10),随后K行,每行给出一位客户的需求,即始发地的编号和目的地的编号,中间以一空格分隔。
输出格式:
处理每一位客户的需求。如果没有现成的线路可以使其到达目的地,就在一行中输出“Sorry, no line is available.”;如果目的地可达,则首先在一行中输出最顺畅路线的经停站数量(始发地和目的地不包括在内),然后按下列格式给出旅行路线:
Go by the line of company #X1 from S1 to S2.
Go by the line of company #X2 from S2 to S3.
......
其中Xi是线路承包公司的编号,Si是经停站的编号。但必须只输出始发地、换乘点和目的地,不能输出中间的经停站。题目保证满足要求的路线是唯一的。
输入样例:
4
7 1001 3212 1003 1204 1005 1306 7797
9 9988 2333 1204 2006 2005 2004 2003 2302 2001
13 3011 3812 3013 3001 1306 3003 2333 3066 3212 3008 2302 3010 3011
4 6666 8432 4011 1306
4
3011 3013
6666 2001
2004 3001
2222 6666
输出样例:
2
Go by the line of company #3 from 3011 to 3013.
10
Go by the line of company #4 from 6666 to 1306.
Go by the line of company #3 from 1306 to 2302.
Go by the line of company #2 from 2302 to 2001.
6
Go by the line of company #2 from 2004 to 1204.
Go by the line of company #1 from 1204 to 1306.
Go by the line of company #3 from 1306 to 3001.
Sorry, no line is available.代码
暂时还没写完