描述
Background
Hello Earthling. We're from the planet Regetni and need your help to make lots of money. Maybe we'll even give you some of it.
You
see, the problem is that in our world, everything is about integers.
It's even enforced by law. No other numbers are allowed for anything.
That said, it shouldn't surprise you that we use integer coordinate
systems to plan our cities. So far only axis-aligned rectangular plots
of land have been sold, but our professor Elgnairt recently had the
revolutionary idea to sell triangular plots, too. We believe that the
high society will love this concept and it'll make us rich.
Unfortunately
the professor patented his idea and thus we can't just do it. We need
his permission and since he's a true scientist, he won't give it to us
before we solve some damn riddle. Here's where you come in,because we
heard that you're a genius.
Problem
The professor's riddle
goes like this: Given some possible corners for the triangles, determine
how many triangles with integral size can be built with them.
Degenerated triangles with empty area (i.e. lines) have to be counted,
too, since 0 is an integer. To be more precise, count the number of
triangles which have as corners three different points from the input
set of points. All points in a scenario will be distinct, i.e. there
won't be duplicates. Here are some examples:
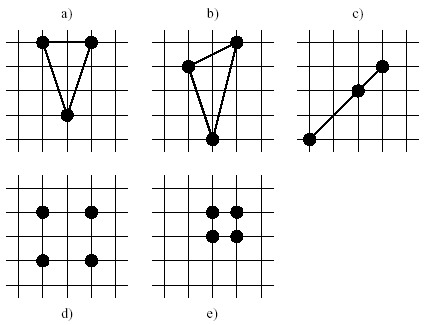
Example a) shows a triangle with integral area (namely 3), b) shows one with non-integral size, c) shows a degenerated triangle with empty area (i.e. zero, so count it!), d) shows four points of which you can choose any three to build an integral area triangle and e) shows four points where you can't build any integral area triangles at all.
Hint: The area A of a triangle with corners (x1, y1), (x2, y2) and (x3, y3) can be computed like this:
A=|x1y2 - y1x2 + x2y3 - y2x3 + x3y1 - y3x1|/2
Try to make clever use of this formula.
输入
The first line contains the number of scenarios. For each scenario, there is one line containing first the number N of distinct points in that scenario (0 <= N <= 10000) and after that N pairs of integers, each pair describing one point (xi, yi) with -100000 <= xi, yi <= 100000. All these numbers are separated by single blanks.
输出
Start the output for every scenario with a line containing "Scenario #i:", where i is the number of the scenario starting at 1. Then print a single line containing the number of triangles with integral area whose three distinct corners are among the points given. Terminate the output for each scenario with a blank line.
样例输入
6
3 0 0 2 0 1 -3
3 0 0 2 1 1 -3
3 0 0 2 2 3 3
4 0 0 2 0 0 2 2 2
4 0 0 1 0 0 1 1 1
9 0 0 0 1 0 2 1 0 1 1 1 2 2 0 2 1 2 2
样例输出
Scenario #1:
1
Scenario #2:
0
Scenario #3:
1
Scenario #4:
4
Scenario #5:
0
Scenario #6:
48
题意
给你N个点,求三角形面积为整数的总数
题解
A=|x1y2 - y1x2 + x2y3 - y2x3 + x3y1 - y3x1|/2
要使公式为整数,|x1y2 - y1x2 + x2y3 - y2x3 + x3y1 - y3x1|为偶
三个点P(x1,y1),Q(x2,y2),C(x3,y3)
可以发现上面的公式和PQC三点的x和y的奇偶性有关
令0=x偶y偶,1=x偶y奇,2=x奇y偶,3=x奇y奇。
打表完后利用组合数求个和。
代码
1 #include<bits/stdc++.h> 2 using namespace std; 3 4 struct point 5 { 6 int p,q,c; 7 bool operator<(const point &d)const{ 8 if(p<d.p)return true; 9 else if(p==d.p) 10 { 11 if(q<d.q)return true; 12 else if(q==d.q) 13 { 14 if(c<d.c)return true; 15 } 16 } 17 return false; 18 } 19 }; 20 set<point>v; 21 void cs() 22 { 23 pair<int,int>po[4]; 24 po[0]={2,2}; 25 po[1]={2,1}; 26 po[2]={1,2}; 27 po[3]={1,1}; 28 for(int p=0;p<4;p++) 29 for(int q=0;q<4;q++) 30 for(int c=0;c<4;c++) 31 { 32 int x1,x2,x3,y1,y2,y3; 33 x1=po[p].first;y1=po[p].second; 34 x2=po[q].first;y2=po[q].second; 35 x3=po[c].first;y3=po[c].second; 36 if((x1*y2-y1*x2+x2*y3-y2*x3+x3*y1-y3*x1)%2==0) 37 { 38 int d[4]; 39 d[0]=p; 40 d[1]=q; 41 d[2]=c; 42 sort(d,d+3); 43 v.insert({d[0],d[1],d[2]}); 44 } 45 } 46 } 47 long long C(int n,int m) 48 { 49 if(m>n)return 0; 50 long long sum=1; 51 for(int i=1;i<=m;i++) 52 sum=sum*(n-i+1)/i; 53 return sum; 54 } 55 int main() 56 { 57 cs(); 58 int t,n,ca=1; 59 scanf("%d",&t); 60 while(t--) 61 { 62 int d[4]={0}; 63 scanf("%d",&n); 64 for(int i=0;i<n;i++) 65 { 66 int x,y; 67 scanf("%d%d",&x,&y); 68 if(x%2==0&&y%2==0)d[0]++; 69 if(x%2==0&&y%2!=0)d[1]++; 70 if(x%2!=0&&y%2==0)d[2]++; 71 if(x%2!=0&&y%2!=0)d[3]++; 72 } 73 long long sum=0; 74 for(auto x:v) 75 { 76 int p=x.p; 77 int q=x.q; 78 int c=x.c; 79 printf("%d %d %d ",p,q,c); 80 int f[4]={0}; 81 f[p]++;f[q]++;f[c]++; 82 sum+=C(d[0],f[0])*C(d[1],f[1])*C(d[2],f[2])*C(d[3],f[3]); 83 } 84 printf("Scenario #%d: %lld ",ca++,sum); 85 } 86 return 0; 87 }