Redis数据类型

五大数据类型

string (动态字符串)

hash （哈希表、压缩链表）

list （双端链表、压缩链表）

set （哈希表、整数集合）

zset （跳表、压缩链表）

动态字符串

存储数字用int类型编码（8字节长整型）、存非数字小于39字节用embstr、大于39字节大于用raw编码。

struct sdsdr{
	int len;// o(1)时间获取字符长度  空间换时间
	int free; // 惰性释放， 将多余的内存记录下来
	char buf[]; 
}

压缩链表

ziplist的结构

...

• zlbytes：32bit无符号整数，表示ziplist占用的字节总数（包括本身占用的4个字节）；
• zltail：32bit无符号整数，记录最后一个entry的偏移量，方便快速定位到最后一个entry；
• zllen：16bit无符号整数，记录entry的个数；
• entry：存储的若干个元素，可以为字节数组或者整数；
• zlend：ziplist最后一个字节，是一个结束的标记位，值固定为255。

// 假设char *zl 指向ziplist首地址
// 指向zlbytes字段
#define ZIPLIST_BYTES(zl)       (*((uint32_t*)(zl)))

// 指向zltail字段(zl+4)
#define ZIPLIST_TAIL_OFFSET(zl) (*((uint32_t*)((zl)+sizeof(uint32_t))))

// 指向zllen字段(zl+(4*2))
#define ZIPLIST_LENGTH(zl)      (*((uint16_t*)((zl)+sizeof(uint32_t)*2)))

// 指向ziplist中尾元素的首地址
#define ZIPLIST_ENTRY_TAIL(zl)  ((zl)+intrev32ifbe(ZIPLIST_TAIL_OFFSET(zl)))

// 指向zlend字段，指恒为255（0xFF）
#define ZIPLIST_ENTRY_END(zl)   ((zl)+intrev32ifbe(ZIPLIST_BYTES(zl))-1)

entry的结构

<prevlen> <encoding> <entry-data>

• prevlen：前一个元素的字节长度，便于快速找到前一个元素的首地址，假如当前元素的首地址是x，那么(x-prevlen)就是前一个元素的首地址。

• encoding：当前元素的编码，Redis根据encoding字段的前两位来判断存储的数据是字符串（字节数组）还是整型，如果是字符串，还可以通过encoding字段的前两位来判断字符串的长度；如果是整形，则要通过后面的位来判断具体长度；

  1. 00xxxxxx 最大长度位 63 的短字符串，后面的6个位存储字符串的位数；
  2. 01xxxxxx xxxxxxxx 中等长度的字符串，后面14个位来表示字符串的长度；
  3. 10000000 aaaaaaaa bbbbbbbb cccccccc dddddddd 特大字符串，需要使用额外 4 个字节来表示长度。第一个字节前缀是10，剩余 6 位没有使用，统一置为零；
  4. 11000000 表示 int16；
  5. 11010000 表示 int32；
  6. 11100000 表示 int64；
  7. 11110000 表示 int24；
  8. 11111110 表示 int8；
  9. 11111111 表示 ziplist 的结束，也就是 zlend 的值 0xFF；
  10. 1111xxxx 表示极小整数，xxxx 的范围只能是 (0001~1101), 也就是1~13。

• entry-data：实际存储的数据。

/* We use this function to receive information about a ziplist entry.
 * Note that this is not how the data is actually encoded, is just what we
 * get filled by a function in order to operate more easily. */
typedef struct zlentry {
    unsigned int prevrawlensize; /* Bytes used to encode the previous entry len*/
    unsigned int prevrawlen;     /* Previous entry len. */
    unsigned int lensize;        /* Bytes used to encode this entry type/len.
                                    For example strings have a 1, 2 or 5 bytes
                                    header. Integers always use a single byte.*/
    unsigned int len;            /* Bytes used to represent the actual entry.
                                    For strings this is just the string length
                                    while for integers it is 1, 2, 3, 4, 8 or
                                    0 (for 4 bit immediate) depending on the
                                    number range. */
    unsigned int headersize;     /* prevrawlensize + lensize. */
    unsigned char encoding;      /* Set to ZIP_STR_* or ZIP_INT_* depending on
                                    the entry encoding. However for 4 bits
                                    immediate integers this can assume a range
                                    of values and must be range-checked. */
    unsigned char *p;            /* Pointer to the very start of the entry, that
                                    is, this points to prev-entry-len field. */
} zlentry;

我们看到结构体定义了7个字段，而上面entry结构体3个字段。回顾压缩列表元素的编码结构，可变因素实际上不止三个；previous_entry_length字段的长度（字段prevrawlensize表示）、previous_entry_length字段存储的内容（字段prevrawlen表示）、encoding字段的长度（字段lensize表示）、encoding字段的内容（字段len表示数据内容长度，字段encoding表示数据类型）、和当前元素首地址（字段p表示）。而headersize字段则表示当前元素的首部长度，即previous_entry_length字段长度与encoding字段长度之和。

创建压缩列表

创建压缩列表的API定义如下，函数无输入参数，返回参数为压缩列表首地址：

unsigned char *ziplistNew(void);
创建空的压缩列表，只需要分配初始存储空间（11=4+4+2+1个字节），并对zlbytes、zltail、zllen和zlend字段初始化即可。
unsigned char *ziplistNew(void) {
    //ZIPLIST_HEADER_SIZE = zlbytes + zltail + zllen;
    unsigned int bytes = ZIPLIST_HEADER_SIZE+1;        
    unsigned char *zl = zmalloc(bytes);
 
    ZIPLIST_BYTES(zl) = intrev32ifbe(bytes);
    ZIPLIST_TAIL_OFFSET(zl) = intrev32ifbe(ZIPLIST_HEADER_SIZE);
    ZIPLIST_LENGTH(zl) = 0;
    
    //结尾标识0XFF
    zl[bytes-1] = ZIP_END;             
    return zl;
}

插入元素

压缩列表插入元素的API定义如下，函数输入参数zl表示压缩列表首地址，p指向新元素的插入位置，s表示数据内容，slen表示数据长度，返回参数为压缩列表首地址。

unsigned char *ziplistInsert(unsigned char *zl, unsigned char *p, unsigned char *s, unsigned int slen);

插入元素时，可以简要分为三个步骤：第一步需要将元素内容编码为压缩列表的元素，第二步重新分配空间，第三步拷贝数据。下面分别讨论每个步骤的实现逻辑。

• 1. 编码

编码即计算previous_entry_length字段、encoding字段和content字段的内容。如何获取前一个元素的长度呢？这时候就需要根据插入元素的位置分情况讨论了，如图所示：

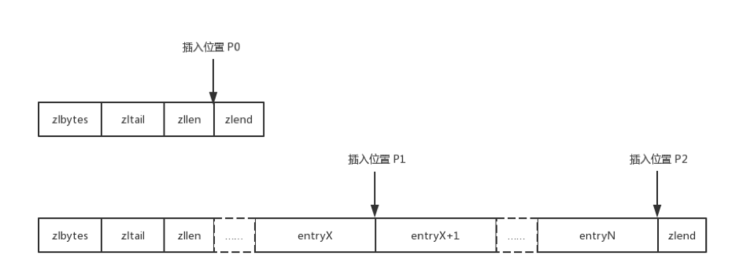
当压缩列表为空插入位置为P0时，此时不存在前一个元素，即前一个元素的长度为0；
  当插入位置为P1时，此时需要获取entryX元素的长度，而entryX+1元素的previous_entry_length字段存储的就是entryX元素的长度，比较容易获取；
  当插入位置为P2时，此时需要获取entryN元素的长度，entryN是压缩列表的尾元素，计算其元素长度需要将其三个字段长度相加，函数实现如下：

unsigned int zipRawEntryLength(unsigned char *p) {
    unsigned int prevlensize, encoding, lensize, len;
    ZIP_DECODE_PREVLENSIZE(p, prevlensize);
    ZIP_DECODE_LENGTH(p + prevlensize, encoding, lensize, len);
    return prevlensize + lensize + len;
}

其中ZIP_DECODE_PREVLENSIZE和ZIP_DECODE_LENGTH在2.2节已经讲过，这里不再赘述。
  encoding字段标识的是当前元素存储的数据类型以及数据长度，编码时首先会尝试将数据内容解析为整数，如果解析成功则按照压缩列表整数类型编码存储，解析失败的话按照压缩列表字节数组类型编码存储。

if (zipTryEncoding(s,slen,&value,&encoding)) {
    reqlen = zipIntSize(encoding);
} else {
    reqlen = slen;
}
 
reqlen += zipStorePrevEntryLength(NULL,prevlen);
reqlen += zipStoreEntryEncoding(NULL,encoding,slen);

程序首先尝试按照整数解析新添加元素的数据内容，数值存储在变量value，编码存储在变量encoding。如果解析成功，还需要计算整数所占字节数。
  变量reqlen最终存储的是当前元素所需空间大小，初始赋值为元素content字段所需空间大小，再累加previous_entry_length所需空间大小与encoding字段所需空间大小。

• 2. 重新分配空间

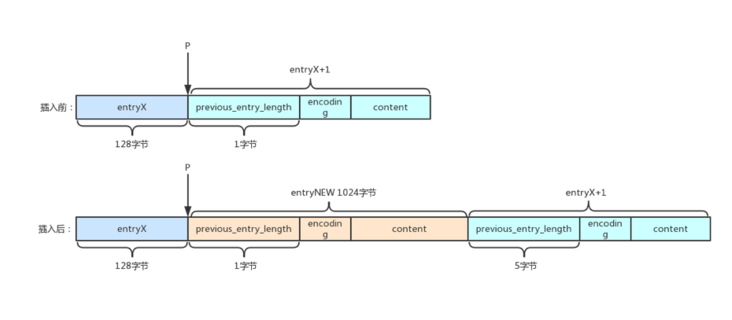
由于新插入元素，压缩列表所需空间增大，因此需要重新分配存储空间。那么空间大小是否是添加元素前的压缩列表长度与新添加元素元素长度之和呢？并不完全是，如图中所示的例子。
  插入元素前，entryX元素长度为128字节，entryX+1元素的previous_entry_length字段占1个字节；添加元素entryNEW元素，元素长度为1024字节，此时entryX+1元素的previous_entry_length字段需要占5个字节；即压缩列表的长度不仅仅是增加了1024字节，还有entryX+1元素扩展的4字节。我们很容易知道，entryX+1元素长度可能增加4字节，也可能减小4字节，也可能不变。而由于重新分配空间，新元素插入的位置指针P会失效，因此需要预先计算好指针P相对于压缩列表首地址的偏移量，待分配空间之后再偏移即可。

size_t curlen = intrev32ifbe(ZIPLIST_BYTES(zl));
 
int forcelarge = 0;
nextdiff = (p[0] != ZIP_END) ? zipPrevLenByteDiff(p,reqlen) : 0;
if (nextdiff == -4 && reqlen < 4) {
    nextdiff = 0;
    forcelarge = 1;
}
 
//存储偏移量
offset = p-zl;
//调用realloc重新分配空间
zl = ziplistResize(zl,curlen+reqlen+nextdiff);
//重新偏移到插入位置P
p = zl+offset;

那么nextdiff与forcelarge在这里有什么用呢？分析ziplistResize函数的3个输入参数，curlen表示插入元素前压缩列表的长度，reqlen表示插入元素元素的长度，而nextdiff表示的是entryX+1元素长度的变化，取值可能为0（长度不变）、4（长度增加4）和-4（长度减小4）。我们再思考下，当nextdiff等于-4，而reqlen小于4时会发生什么呢？没错，插入元素导致压缩列表所需空间减少了，即函数ziplistResize底层调用realloc重新分配的空间小于指针zl指向的空间。这可能会存在问题，我们都知道realloc重新分配空间时，返回的地址可能不变，当重新分配的空间大小反而减少时，realloc底层实现可能会将多余的空间回收，此时可能会导致数据的丢失。因此需要避免这种情况的发生，即重新赋值nextdiff等于0，同时使用forcelarge标记这种情况。
  可以再思考下，nextdiff等于-4时，reqlen会小于4吗？答案是可能的，连锁更新可能会导致这种情况的发生。连锁更新将在第4节介绍。

• 3. 数据拷贝

重新分配空间之后，需要将位置P后的元素移动到指定位置，将新元素插入到位置P。我们假设entryX+1元素的长度增加4（即nextdiff等于4），此时数据拷贝示意图如图所示：

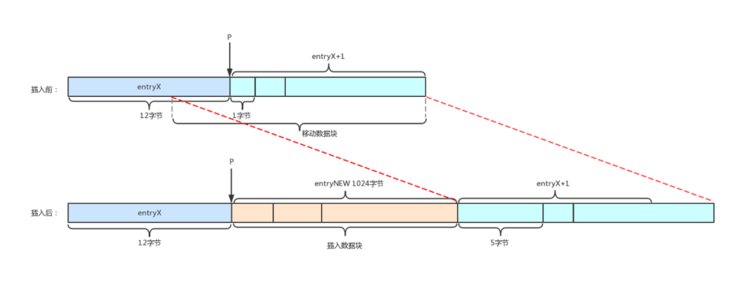
从图中可以看到，位置P后的所有元素都需要移动，移动的偏移量是插入元素entryNew的长度，移动的数据块长度是位置P后所有元素长度之和再加上nextdiff的值，数据移动之后还需要更新entryX+1元素的previous_entry_length字段。

memmove(p+reqlen,p-nextdiff,curlen-offset-1+nextdiff); 
//更新entryX+1元素的previous_entry_length字段字段
if (forcelarge)
    //entryX+1元素的previous_entry_length字段依然占5个字节;
    //但是entryNEW元素长度小于4字节
    zipStorePrevEntryLengthLarge(p+reqlen,reqlen);
else
    zipStorePrevEntryLength(p+reqlen,reqlen);
 
//更新zltail字段
ZIPLIST_TAIL_OFFSET(zl) =
    intrev32ifbe(intrev32ifbe(ZIPLIST_TAIL_OFFSET(zl))+reqlen);
 
zipEntry(p+reqlen, &tail);
if (p[reqlen+tail.headersize+tail.len] != ZIP_END) {
    ZIPLIST_TAIL_OFFSET(zl) =
        intrev32ifbe(intrev32ifbe(ZIPLIST_TAIL_OFFSET(zl))+nextdiff);
}
 
//更新zllen字段
ZIPLIST_INCR_LENGTH(zl,1);

思考一下，第一次更新尾元素偏移量之后，为什么指向的元素可能不是尾元素呢？很显然，当entryX+1元素就是尾元素时，只需要更新一次尾元素的偏移量；但是当entryX+1元素不知尾元素，且entryX+1元素长度发生了改变，此时尾元素偏移量还需要加上nextdiff的值。

删除元素

压缩列表删除元素的API定义如下，函数输入参数zl指向压缩列表首地址，*p指向待删除元素的首地址（参数p同时可以作为输出参数），返回参数为压缩列表首地址。

unsigned char *ziplistDelete(unsigned char *zl, unsigned char **p);

ziplistDelete函数只是简单调用底层__ziplistDelete函数实现删除功能；__ziplistDelete函数可以同时删除多个元素，输入参数p指向的是首个删除元素的首地址，num表示待删除元素数目。

unsigned char *ziplistDelete(unsigned char *zl, unsigned char **p) {
    size_t offset = *p-zl;
    zl = __ziplistDelete(zl,*p,1);
    *p = zl+offset;
    return zl;
}

删除元素同样可以简要分为三个步骤：第一步计算待删除元素总长度，第二步数据拷贝，第三步重新分配空间。下面分别讨论每个步骤的实现逻辑。

• 1. 计算待删除元素总长度，其中zipRawEntryLength函数在3.2节已经讲过，这里不再详述；

//解码第一个待删除元素
zipEntry(p, &first);
 
//遍历所有待删除元素，同时指针p向后偏移
for (i = 0; p[0] != ZIP_END && i < num; i++) {
    p += zipRawEntryLength(p);
    deleted++;
}
//totlen即为待删除元素总长度
totlen = p-first.p;

• 2. 数据拷贝；

第一步骤计算完成之后，指针first与指针p之间的元素都是待删除的。很显然，当指针p恰好指向zlend字段，不再需要数据的拷贝了，只需要更新尾节点的偏移量即可。下面分析另外一种情况，即指针p指向的是某一个元素而不是zlend字段。
分析类似于3.2节插入元素。删除元素时，压缩列表所需空间减少，减少的量是否仅仅是待删除元素总长度呢？答案同样是否定的，举个简单的例子，下图是经过第一步骤计算之后的示意图：

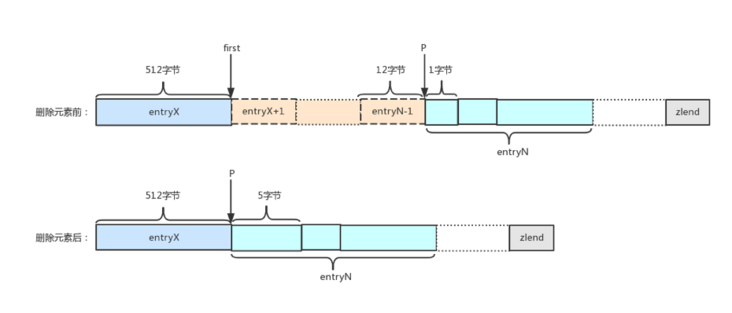
删除元素entryX+1到元素entryN-1之间的N-X-1个元素，元素entryN-1的长度为12字节，因此元素entryN的previous_entry_length字段占1个字节；删除这些元素之后，entryX称为了entryN的前一个元素，元素entryX的长度为512字节，因此元素entryN的previous_entry_length字段需要占5个字节。即删除元素之后的压缩列表的总长度，还与entryN元素长度的变化量有关。

//计算元素entryN长度的变化量
nextdiff = zipPrevLenByteDiff(p,first.prevrawlen);
 
//更新元素entryN的previous_entry_length字段
p -= nextdiff;
zipStorePrevEntryLength(p,first.prevrawlen);
 
//更新zltail
ZIPLIST_TAIL_OFFSET(zl) =
    intrev32ifbe(intrev32ifbe(ZIPLIST_TAIL_OFFSET(zl))-totlen);
 
zipEntry(p, &tail);
if (p[tail.headersize+tail.len] != ZIP_END) {
    ZIPLIST_TAIL_OFFSET(zl) =
       intrev32ifbe(intrev32ifbe(ZIPLIST_TAIL_OFFSET(zl))+nextdiff);
}
 
//数据拷贝
memmove(first.p,p,
    intrev32ifbe(ZIPLIST_BYTES(zl))-(p-zl)-1);

与3.2节插入元素更新zltail字段相同，当entryX+1元素就是尾元素时，只需要更新一次尾元素的偏移量；但是当entryX+1元素不是尾元素时，且entryX+1元素长度发生了改变，此时尾元素偏移量还需要加上nextdiff的值。

• 3. 重新分配空间

逻辑与3.2节插入元素逻辑基本类似，这里就不再详述。代码如下：

offset = first.p-zl;
zl = ziplistResize(zl, intrev32ifbe(ZIPLIST_BYTES(zl))-totlen+nextdiff);
p = zl+offset;
ZIPLIST_INCR_LENGTH(zl,-deleted);

思考一下：在3.2节我们提到，调用ziplistResize函数重新分配空间时，如果重新分配的空间小于指针zl指向的空间大小时，可能会出现问题。而这里由于是删除元素，压缩列表的长度肯定是减少的。为什么又能这样使用呢？
根本原因在于删除元素时，我们是先拷贝数据，再重新分配空间，即调用ziplistResize函数时，多余的那部分空间存储的数据已经被拷贝了，此时回收这部分空间并不会造成数据的丢失。

遍历压缩列表

遍历就是从头到尾（前向遍历）或者从尾到头（后向遍历）访问压缩列表中的每一个元素。压缩列表的遍历API定义如下，函数输入参数zl指向压缩列表首地址，p指向当前访问元素的首地址；ziplistNext函数返回后一个元素的首地址，ziplistPrev返回前一个元素的首地址。

//后向遍历
unsigned char *ziplistNext(unsigned char *zl, unsigned char *p);
//前向遍历
unsigned char *ziplistPrev(unsigned char *zl, unsigned char *p);

我们已经知道压缩列表每个元素的previous_entry_length字段存储的是前一个元素的长度，因此压缩列表的前向遍历相对简单，表达式(p-previous_entry_length)即可获取前一个元素的首地址，这里不做详述。后向遍历时，需要解码当前元素，计算当前元素长度，才能获取后一个元素首地址；ziplistNext函数实现如下：

unsigned char *ziplistNext(unsigned char *zl, unsigned char *p) {
    //zl参数无用；这里只是为了避免警告
    ((void) zl);
 
    if (p[0] == ZIP_END) {
        return NULL;
    }
 
    p += zipRawEntryLength(p);
    if (p[0] == ZIP_END) {
        return NULL;
    }
 
    return p;
}

连锁更新

如下图所示，删除压缩列表zl1位置P1的元素entryX，或者在压缩列表zl2位置P2插入元素entryY，此时会出现什么情况呢？

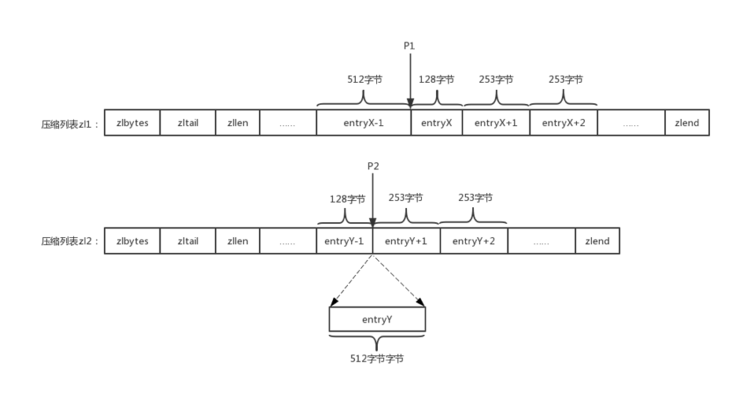
压缩列表zl1，元素entryX之后的所有元素entryX+1、entryX+2等长度都是253字节，显然这些元素的previous_entry_length字段的长度都是1字节。当删除元素entryX时，元素entryX+1的前驱节点改为元素entryX-1，长度为512字节，此时元素entryX+1的previous_entry_length字段需要5字节才能存储元素entryX-1的长度，则元素entryX+1的长度需要扩展至257字节；而由于元素entryX+1长度的增加，元素entryX+2的previous_entry_length字段同样需要改变。以此类推，由于删除了元素entryX，之后的所有元素entryX+1、entryX+2等长度都必须扩展，而每次元素的扩展都将导致重新分配内存，效率是很低下的。压缩列表zl2，插入元素entryY同样会产生上面的问题。
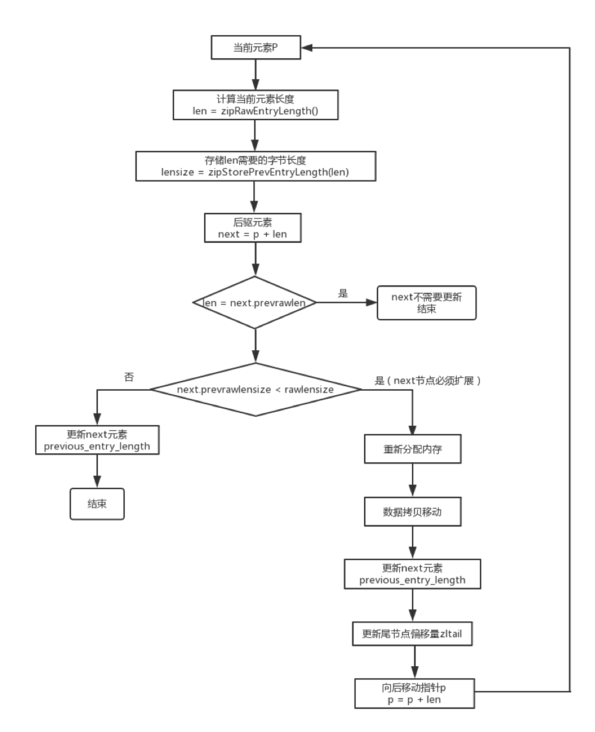
  上面的情况称之为连锁更新。从上面分析可以看出，连锁更新会导致多次重新分配内存以及数据拷贝，效率是很低下的。但是出现这种情况的概率是很低的，因此对于删除元素与插入元素的操作，redis并没有为了避免连锁更新而采取措施。redis只是在删除元素与插入元素操作的末尾，检查是否需要更新后续元素的previous_entry_length字段，其实现函数_ziplistCascadeUpdate，主要逻辑如下图所示：

https://segmentfault.com/a/1190000017328042

哈希表

//散列函数 伪代码 
int Hash(string key) {
  // 获取后四位字符
  string hashValue =int.parse(key.Substring(key.Length-4, 4));
  // 将后两位字符转换为整数
  return hashValue;
}

key通过哈希函数计算 得出数据所在位置 o(1) 时间复杂度

跳表

typedef struct zskiplist {
    // 头节点，尾节点
    struct zskiplistNode *header, *tail;
    // 节点数量
    unsigned long length;
    // 目前表内节点的最大层数
    int level;
} zskiplist;

多级索引

基于偶数节点增加索引并且只有两层的情况下，最高层的节点数是n/2，整体来看搜索的复杂度降低为O(n/2)，并不要小看这个1/2的系数，看到这里会想 增加索引层数到k，那么复杂度将指数降低为O(n/2^k)。

索引层数不是无休止增加的，取决于该层索引的节点数量，如果该层的索引的节点数量等于2了，那么再往上加层也就没有意义了，画个图看一下：

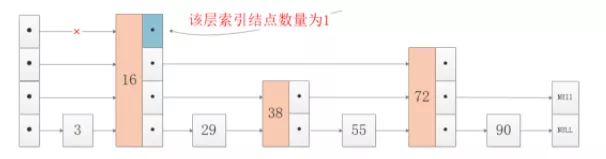
这个非常好理解，如果所在层索引结点只有1个，比如4层索引的结点16，只能顺着16向下遍历，无法向后跳到4层其他结点，因此当所在层索引结点数量等于2，则到达最高索引层，这个约束在分析跳表复杂度时很重要。

索引层数和索引结点密度

跳表的复杂度和索引层数、索引结点的稀疏程度有很大关系。

索引层数我们从上面也看到了，稀疏程度相当于索引结点的数量比例，如果跳表的索引结点数量很少，那么将接近退化为普通链表，这种情况在数据量是较大时非常明显，画图看下(蓝色部分表示有很多结点)：

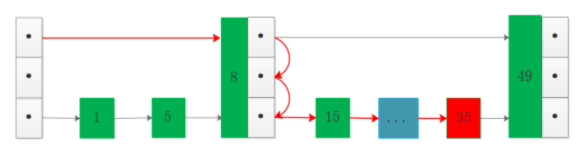
图中可以看到虽然有索引层，但是索引结点数量相对全部数据比例较低，这种情况下搜索35相比无索引情况优势并不明显。

所以跳表的效率和索引层数和索引结点的密度有密切的关系，当然索引结点太多也就等于没有索引了。

太少的索引结点和太多的索引结点都是一样的低效。

复杂度分析

从前面的分析可知，跳表的复杂度和索引层数m以及索引结点间隙d有直接关系，其中索引结点间隙理解为相隔几个结点出现索引结点，体现了对应层索引结点的稀疏程度，在无索引结点时只能遍历无法跳跃。

如何确定最高索引层数m呢？

如果一个链表有 n 个结点，如果每两个结点取出一个结点建立索引，那么第一级索引的结点数是 n/2，第二级索引的结点数是n/4，以此类推第 m 级索引的结点数为 n/(2^m)，前面说过最高层结点数为2，因此存在关系：

算上最底层的原始链表，整个跳表的高度为h=logn(底数为2)，每一层需要遍历的结点数是d，那么整个过程的复杂度为:O(d*logn)。

d表明了层间结点的稀疏程度，也就是每隔2个结点选取索引结点、或者每隔3个结点选取索引结点，每个4个结点选取索引结点......

最密集的情况下d=2，借用知乎某大佬的文章的图片：

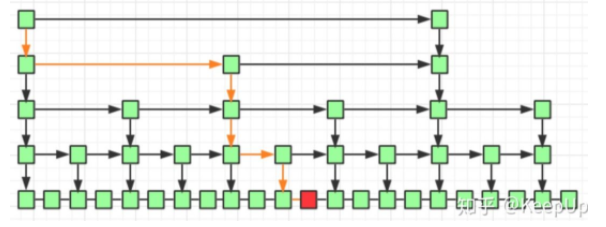
但是索引结点密集也意味着存储空间的增加，跳表相比较普通链表就是典型的用空间换时间的数据结构，这样就达到了AVL的复杂度O(logn)。

跳表的空间存储

以d=2的最密集情况为例，计算跳表的索引结点总数：2+4+8+......n/8+n/4+n/2=n-2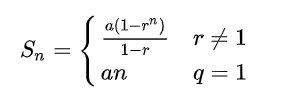

由等比数列求和公式得d=2的跳表额外空间为O(n-2)。

跳表的插入和删除

工程中的跳表并不严格要求索引层结点数量遵循2:1的关系，因为这种要求将导致插入和删除数据时的调整，成本很大.

跳表的每个插入的结点在插入时进行选择是否作为索引结点，如果作为索引结点则随机出层数，整个过程都是基于概率的，但是在大数据量时却能很好地解决索引层数和结点数的权衡。

我们针对插入和删除来看下基本的操作过程吧！

跳表元素17插入：

链表的插入和删除是结合搜索过程完成的，贴一张William Pugh在论文中给出的在跳表中插入元素17的过程图(暂时忽略结点17是否作为索引结点以及索引层数，后面会详细说明)：

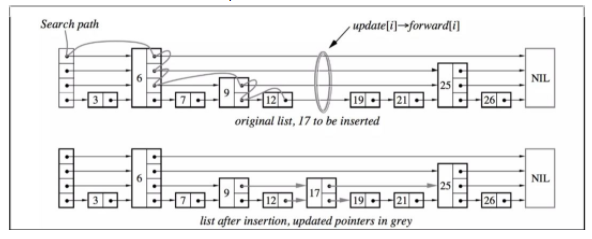
跳表元素1删除：

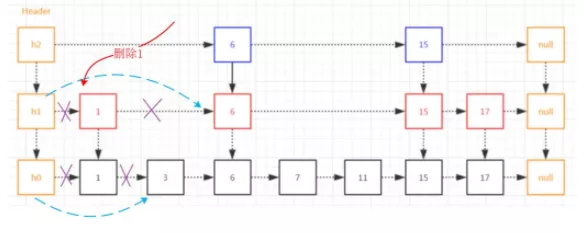
跳表元素的删除与普通链表相比增加了索引层的判断，如果结点是非索引结点则正常处理，如果结点是索引结点那边需要进行索引层结点的处理。

跳跃链表的应用

一般讨论查找问题时首先想到的是平衡树和哈希表，但是跳表这种数据结构也非常犀利，性能和实现复杂度都可以和红黑树媲美，甚至某些场景由于红黑树，从1990年被发明目前广泛应用于多种场景中，包括Redis、LevelDB等数据存储引擎中。

跳表在Redis中的应用

ZSet结构同时包含一个字典和一个跳跃表，跳跃表按score从小到大保存所有集合元素。字典保存着从member到score的映射。这两种结构通过指针共享相同元素的member和score，不会浪费额外内存。

typedef struct zset {
    dict *dict;
    zskiplist *zsl;
} zset;

ZSet中的字典和跳表布局：

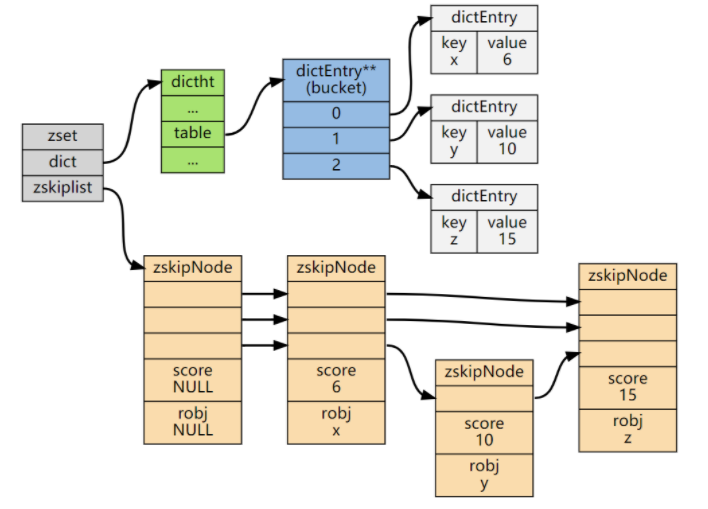
ZSet中跳表的实现细节

随机层数的实现原理

跳表是一个概率型的数据结构，元素的插入层数是随机指定的。Willam Pugh在论文中描述了它的计算过程如下：指定节点最大层数 MaxLevel，指定概率 p， 默认层数 lvl 为1

生成一个0~1的随机数r，若r<p，且lvl<MaxLevel ，则lvl ++

重复第 2 步，直至生成的r >p 为止，此时的 lvl 就是要插入的层数。

论文中生成随机层数的伪码：

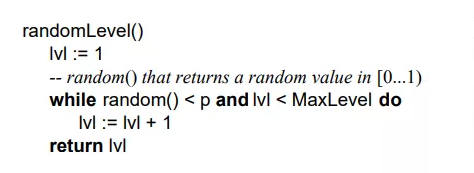
在Redis中对跳表的实现基本上也是遵循这个思想的，只不过有微小差异，看下Redis关于跳表层数的随机源码src/z_set.c：

/* Returns a random level for the new skiplist node we are going to create.
 * The return value of this function is between 1 and ZSKIPLIST_MAXLEVEL
 * (both inclusive), with a powerlaw-alike distribution where higher
 * levels are less likely to be returned. */
int zslRandomLevel(void) {
    int level = 1;
    while ((random()&0xFFFF) < (ZSKIPLIST_P * 0xFFFF))
        level += 1;
    return (level<ZSKIPLIST_MAXLEVEL) ? level : ZSKIPLIST_MAXLEVEL;
}

其中两个宏的定义在redis.h中：

#define ZSKIPLIST_MAXLEVEL 32 /* Should be enough for 2^32 elements */
#define ZSKIPLIST_P 0.25      /* Skiplist P = 1/4 */

可以看到while中的：

(random()&0xFFFF) < (ZSKIPLIST_P*0xFFFF)

跳表结点的平均层数

我们很容易看出，产生越高的节点层数出现概率越低，无论如何层数总是满足幂次定律越大的数出现的概率越小。

如果某件事的发生频率和它的某个属性成幂关系，那么这个频率就可以称之为符合幂次定律。

幂次定律的表现是少数几个事件的发生频率占了整个发生频率的大部分， 而其余的大多数事件只占整个发生频率的一个小部分。

幂次定律应用到跳表的随机层数来说就是大部分的节点层数都是黄色部分，只有少数是绿色部分，并且概率很低。

定量的分析如下：

• 节点层数至少为1，大于1的节点层数满足一个概率分布。
• 节点层数恰好等于1的概率为p^0(1-p)
• 节点层数恰好等于2的概率为p^1(1-p)
• 节点层数恰好等于3的概率为p^2(1-p)
• 节点层数恰好等于4的概率为p^3(1-p)

依次递推节点层数恰好等于K的概率为p^(k-1)(1-p)

因此如果我们要求节点的平均层数，那么也就转换成了求概率分布的期望问题了，灵魂画手的我再次上线：

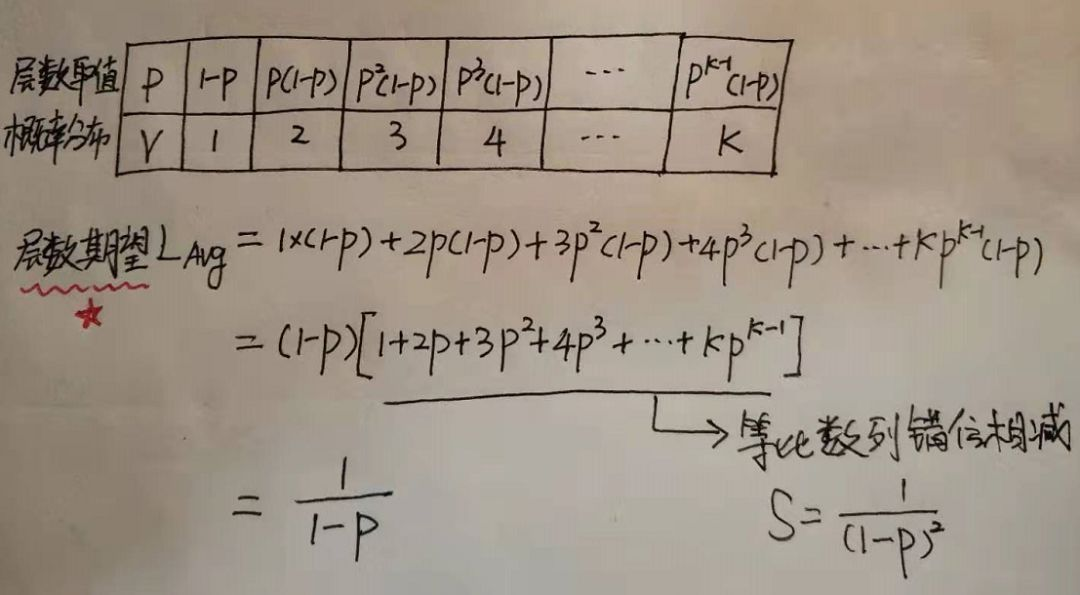
表中P为概率，V为对应取值，给出了所有取值和概率的可能，因此就可以求这个概率分布的期望了。

方括号里面的式子其实就是高一年级学的等比数列，常用技巧错位相减求和，从中可以看到结点层数的期望值与1-p成反比。

对于Redis而言，当p=0.25时结点层数的期望是1.33。

在Redis源码中有详尽的关于插入和删除调整跳表的过程，本文就不再展开了，代码并不算难懂，都是纯C写的没有那么多炫技的特效，放心大胆读起来。

双端链表

typedef struct list { 
listNode *head; //链表头结点指针 
listNode *tail; //链表尾结点指针
unsigned long len; //链表长度计数器
 
//下面的三个函数指针就像类中的成员函数一样
void *(*dup)(void *ptr); //复制链表节点保存的值 
void (*free)(void *ptr); //释放链表节点保存的值
int (*match)(void *ptr, void *key); //比较链表节点所保存的节点值和另一个输入的值是否相等 
} list

typedef struct listNode {
 struct listNode *prev; //前驱节点，如果是list的头结点，则prev指向NULL 
 struct listNode *next;//后继节点，如果是list尾部结点，则next指向NULL 
 void *value; //万能指针，能够存放任何信息 
} listNode

集合

Set 集合采用了整数集合和字典两种方式来实现的，当满足如下两个条件的时候，采用整数集合实现；一旦有一个条件不满足时则采用字典来实现。

• Set 集合中的所有元素都为整数
• Set 集合中的元素个数不大于 512（默认 512，可以通过修改 set-max-intset-entries 配置调整集合大小）

整数集合实现原理图

整数集合

整数集合(intset)是Redis用于保存整数值的集合抽象数据结构,它可以保存类型为int16_t、int32_t或者int64_t的整数值,并且保证集合中不会出现重复元素。

//每个intset结构表示一个整数集合
typedef struct intset{
    //编码方式
    uint32_t encoding;
    //集合中包含的元素数量
    uint32_t length;
    //保存元素的数组
    int8_t contents[];
} intset;

• contents数组是整数集合的底层实现，整数集合的每个元素都是 contents数组的个数组项(item),各个项在数组中按值的大小从小到大有序地排列,并且数组中不包含任何重复项。
• length属性记录了数组的长度。
• intset结构将contents属性声明为int8_t类型的数组,但实际上 contents数组并不保存任何int8t类型的值, contents数组的真正类型取决于encoding属性的值。encoding属性的值为INTSET_ENC_INT16则数组就是uint16_t类型，数组中的每一个元素都是int16_t类型的整数值(-32768——32767)，encoding属性的值为INTSET_ENC_INT32则数组就是uint32_t类型，数组中的每一个元素都是int16_t类型的整数值(-2147483648——2147483647)。

String

存储数字用int类型编码（8字节长整型）、存非数字小于39字节用embstr、大于39字节大于用raw编码。

Hash

ziplist当哈希元素个数小于hash-max-ziplist-entries配置（默认512个），同时所有值都小于hash-max-ziplist-value配置（默认64字节），redis会使用ziplist作为哈希内部实现。

hash-max-ziplist-entries 512  # hash 的元素个数超过 512 就必须用标准结构存储
hash-max-ziplist-value 64  # hash 的任意元素的 key/value 的长度超过 64 就必须用标准结构存储

hashtable当哈希类型无法满足ziplist的条件时， redis会使用hashtable作为内部实现。

Zset

ziplist

zset-max-ziplist-entries 128  # zset 的元素个数超过 128 就必须用标准结构存储
zset-max-ziplist-value 64  # zset 的任意元素的长度超过 64 就必须用标准结构存储

skiplist

Set

intset

普通set

List

ziplist

双端链表

扩展类型

geo

bighash

loglog