python: MNIST-神经网络的自主学习

问题：如何实现数字“5”的识别？O(∩_∩)O~

                                 手写数字“5”的例子：写法因人而异，五花八门

方案： 从图像中提取特征量-----用及其学习技术学习这些特征量的模式

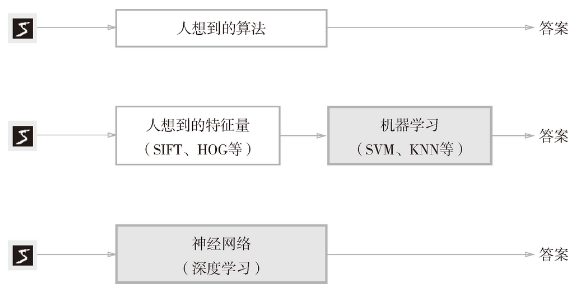
神经网络的学习中所用到的指标称为损失函数。

可以用作损失函数的函数很多，最有名的是均方误差（mean squared error）。

　　均方误差的表达式：

　　　　

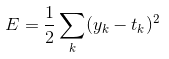
　　　　y_k  -----------神经网络输出

　　　　t_k  -----------监督数据，one-hot表示

　　这里的神经网络的输出y是softmax函数的输出。softmax函数的输出可以理解为概率。

　　用python实现均方误差：　　　

def mean_squared_error(y-t):
    return 0.5*np.sum((y-t)**2)

除了均方误差，交叉熵误差（cross entropy error）也经常被用作损失函数。
　　交叉熵误差的表达式：

　　　　

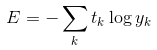
　　　　比如，假设正确解标签的索引是“2”，与之对应的神经网络的输出是 0.6，则交叉熵误差是 -log 0.6 = 0.51；若“2”对应的输出是 0.1，则交叉熵误差为 -log 0.1 = 2.30。也就是说，交叉熵误差的值是由正确解标签所对应的输出结果决定的。

自然对数的图像如图所示：

import matplotlib.pyplot as plt
import numpy as np

#生成数据
x=np.arange(0.01,1.01,0.01)
y=np.log(x)

#绘制图像
plt.plot(x,y)
plt.xlabel('x')
plt.ylabel('y')
plt.show()

代码实现交叉熵误差：

def cross_entropy_error(y,t):
    delta=1e-7
    return -np.sum(t*np.log(y+delta))

 

如果计算所有训练数据的损失函数的综合，则公式为：

　　

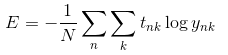
上述的损失函数都是针对单个数据，加入训练数据一共有6000个，那我们每次拿出100个当做是6000的近似计算一次，这样计算得到的结果就是mini-batch学习的结果。

在之前的笔记中已经知道了读入MNIST数据集的代码，即：

import sys, os
sys.path.append(os.pardir)
import numpy as np
from dataset.mnist import load_mnist

(x_train, t_train), (x_test, t_test) = 
    load_mnist(normalize=True, one_hot_label=True)

print(x_train.shape) # (60000, 784)
print(t_train.shape) # (60000, 10)

mnist数据下载的代码mnist.py如下：

# coding: utf-8
try:
    import urllib.request
except ImportError:
    raise ImportError('You should use Python 3.x')
import os.path
import gzip
import pickle
import os
import numpy as np


url_base = 'http://yann.lecun.com/exdb/mnist/'
key_file = {
    'train_img':'train-images-idx3-ubyte.gz',
    'train_label':'train-labels-idx1-ubyte.gz',
    'test_img':'t10k-images-idx3-ubyte.gz',
    'test_label':'t10k-labels-idx1-ubyte.gz'
}

dataset_dir = os.path.dirname(os.path.abspath(__file__))
save_file = dataset_dir + "/mnist.pkl"

train_num = 60000
test_num = 10000
img_dim = (1, 28, 28)
img_size = 784


def _download(file_name):
    file_path = dataset_dir + "/" + file_name
    
    if os.path.exists(file_path):
        return

    print("Downloading " + file_name + " ... ")
    urllib.request.urlretrieve(url_base + file_name, file_path)
    print("Done")
    
def download_mnist():
    for v in key_file.values():
       _download(v)
        
def _load_label(file_name):
    file_path = dataset_dir + "/" + file_name
    
    print("Converting " + file_name + " to NumPy Array ...")
    with gzip.open(file_path, 'rb') as f:
            labels = np.frombuffer(f.read(), np.uint8, offset=8)
    print("Done")
    
    return labels

def _load_img(file_name):
    file_path = dataset_dir + "/" + file_name
    
    print("Converting " + file_name + " to NumPy Array ...")    
    with gzip.open(file_path, 'rb') as f:
            data = np.frombuffer(f.read(), np.uint8, offset=16)
    data = data.reshape(-1, img_size)
    print("Done")
    
    return data
    
def _convert_numpy():
    dataset = {}
    dataset['train_img'] =  _load_img(key_file['train_img'])
    dataset['train_label'] = _load_label(key_file['train_label'])    
    dataset['test_img'] = _load_img(key_file['test_img'])
    dataset['test_label'] = _load_label(key_file['test_label'])
    
    return dataset

def init_mnist():
    download_mnist()
    dataset = _convert_numpy()
    print("Creating pickle file ...")
    with open(save_file, 'wb') as f:
        pickle.dump(dataset, f, -1)
    print("Done!")

def _change_one_hot_label(X):
    T = np.zeros((X.size, 10))
    for idx, row in enumerate(T):
        row[X[idx]] = 1
        
    return T
    

def load_mnist(normalize=True, flatten=True, one_hot_label=False):
    """读入MNIST数据集
    
    Parameters
    ----------
    normalize : 将图像的像素值正规化为0.0~1.0
    one_hot_label : 
        one_hot_label为True的情况下，标签作为one-hot数组返回
        one-hot数组是指[0,0,1,0,0,0,0,0,0,0]这样的数组
    flatten : 是否将图像展开为一维数组
    
    Returns
    -------
    (训练图像, 训练标签), (测试图像, 测试标签)
    """
    if not os.path.exists(save_file):
        init_mnist()
        
    with open(save_file, 'rb') as f:
        dataset = pickle.load(f)
    
    if normalize:
        for key in ('train_img', 'test_img'):
            dataset[key] = dataset[key].astype(np.float32)
            dataset[key] /= 255.0
            
    if one_hot_label:
        dataset['train_label'] = _change_one_hot_label(dataset['train_label'])
        dataset['test_label'] = _change_one_hot_label(dataset['test_label'])
    
    if not flatten:
         for key in ('train_img', 'test_img'):
            dataset[key] = dataset[key].reshape(-1, 1, 28, 28)

    return (dataset['train_img'], dataset['train_label']), (dataset['test_img'], dataset['test_label']) 


if __name__ == '__main__':
    init_mnist()

minst.py在文件夹dataset中，数据在dataset下的mnist.pkl文件中。

目前我还是自己写不出来这样的代码，还是得分析透才能学会，这里先留一下，下次来分析......

那么，如何从训练数据中随机抽取10笔数据呢？可以使用NumPy的no.random.choice()，携程如下形式：

train_size=x_train.shape[0]
batch_size=10
batch_mask=np.random.choice(train_size,batch_size)
x_batch=x_train[batch_mask]
t_batch=t_train[batch_mask]

mini_batch交叉熵的实现：

def cross_entropy_error(y,t):
    if y.ndim==1:
        t=t.reshape(1,t.size)
        y=y.reshape(1,y.size)
        
    batch_size=y.shape[0]
    return -np.sum(t*np.log(y+1e-7))/batch_size

这里，y 是神经网络的输出，t 是监督数据。y 的维度为 1 时，即求单个数据的交叉熵误差时，需要改变数据的形状。并且，当输入为 mini-batch 时，要用 batch 的个数进行正规化，计算单个数据的平均交叉熵误差。

当监督数据是标签形式而不是one-hot表示时，交叉熵代码如下：

def cross_entropy_error(y,t):
    if y.ndim==1:
        t=t.reshape(1,t.size)
        y=y.reshape(1,y.size)
        
    batch_size=y.shape[0]
    return -np.sum(np.log(y[np.arange(batch_size),t]+1e-7))/batch_size

实现的要点是，由于 one-hot 表示中 t 为 0 的元素的交叉熵误差也为 0，因此针对这些元素的计算可以忽略。换言之，如果可以获得神经网络在正确解标签处的输出，就可以计算交叉熵误差。因此，t 为 one-hot 表示时通过 t * np.log(y) 计算的地方，在 t 为标签形式时，可用 np.log( y[np.arange (batch_size), t] ) 实现相同的处理（为了便于观察，这里省略了微小值1e-7）。

作为参考，简单介绍一下np.log( y[np.arange(batch_size), t] )。np.arange (batch_size) 会生成一个从 0 到 batch_size-1 的数组。比如当 batch_size 为 5 时，np.arange(batch_size) 会生成一个 NumPy 数组 [0, 1, 2, 3, 4]。因为 t 中标签是以 [2, 7, 0, 9, 4] 的形式存储的，所以 y[np.arange(batch_size), t] 能抽出各个数据的正确解标签对应的神经网络的输出（在这个例子中，y[np.arange(batch_size), t] 会生成 NumPy 数组 [y[0,2], y[1,7], y[2,0], y[3,9], y[4,4]]）。

这部分理解起来并不是很容易，还是得多回顾才能真正掌握。均方误差、交叉熵误差以及下载mnist数据集，这些里面后两部分还得在后续的学习中继续补充。

一定要加油啊，向目标前进~~~