消除左递归

FIRST集的求法：

对于文法G的任一符号串α=X1X2…Xn可按下列步骤构造其FIRST(α)集合：

1) 置FIRST(α)=φ

2) 将FIRST(X1)中的一切非ε符号加进FIRST(α)；

3) 若ε∈FIRST(X1)，将FIRST(X2)中的一切非ε符号加进FIRST(α)；若ε∈FIRST(X1)和FIRST(X2)，将FIRST(X3)中的一切非ε符号加进FIRST(α)；依次类推。//根据分析方法中的第3条，若该符号能推出ε则将下一个符号的FIRST集加入FIRST(α)，以此类推。

4)若对于一切1≤i≤n,ε∈FIRST(Xi)，则将ε符号加进FIRST(α)。 //根据分析方法的第4条，若右侧符号串的每个符号都能推出ε，则α肯定能推出ε，所以将ε加进FIRST（α）。

FOLLOW集的计算

1. 对于文法的开始符号S，置#于FOLLOW(S) 中;

2. 若Ａ→αBβ是一个产生式,则把FIRST(β)-{e}加至FOLLOW(B)中;若β=>*e (即eÎFIRST(β))，则把FOLLOW(A)加至FOLLOW(B)中。//若B有可能是最后一个符号，则把

FOLLOW(A)加至FOLLOW(B)中，否则把FIRST(β)- {e}加至FOLLOW(B)中。

反复使用上述规则，直到所求FOLLOW集不再增大为止。

SELECT集：

S->A

如果S不能推出空集 则SELECT(S->A)=FIRST(S)

如果S能推出空集 则SELECT(S->A)=FOLLOW(S)-{ε}

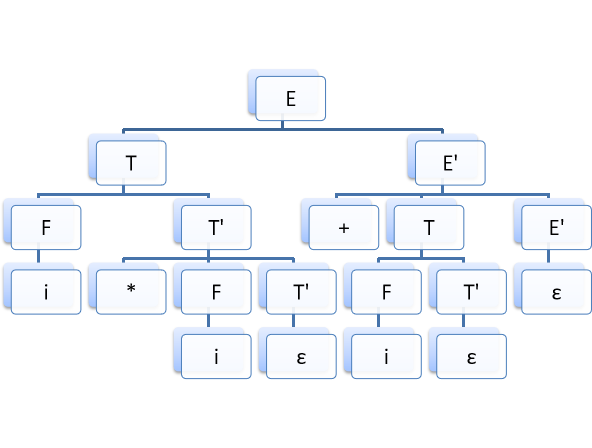
1.将以下文法消除左递归，并分析符号串 i*i+i。

 并分别求FIRST集、FOLLOW集，和SELECT集

     E -> E+T | T

     T -> T*F | F

     F -> (E) | i

消除左递归:

E→TE'

E'→+TE'|ε

T→FT'

T'→*FT'|ε

F→(E)|i

FIRST集:

FIRST(E)→FIRST(T)→FIRST(F)→{ ( , i }

FIRST(E')→{+,ε}

FIRST(T)→FIRST(F)→{ ( , i }

FIRST(T')→{*,ε}

FIRST(F)→{ ( , i }

FOLLOW集:

FOLLOW(E)→{ ) , #  }

FOLLOW(E')→{ ) , # }

FOLLOW(T)→{ + , ) , # }

FOLLOW(T')→{ + , ) , # }

FOLLOW(F)→{ * , + , ) , # }

SELECT集：

SELECT(E→TE')={ ( , i }

SELECT(E'→+TE')={+}

SELECT(E'→ε)={),#}

SELECT(T→FT')={ ( , i }

SELECT(T'→*FT')={*}

SELECT(T'→ε)={+,),#}

SELECT(F→(E))={(}

SELECT(F→i)={i}

分析符号串i*i+i

2.P101练习7（2）（3）文法改写，并分别求FIRST集、FOLLOW集，和SELECT集

(2)A→aABe|a

　B→Bb|d

消除左递归:

A→aA'

A'→ABe|ε

B→dB'

B'→bB'|ε

FIRST集:

FIRST(A)→{a}

FIRST(A')→{a,ε}

FIRST(B)→{d}

FIRST(B')→{b,ε}

FOLLOW集:

FOLLOW(A)→{d,#}

FOLLOW(A')→{d,#}

FOLLOW(B)→{e}

FOLLOW(B')→{e}

 SELECT集：

SELECT(A→aA')={d,#}

SELECT(A'→ABe)={a}

SELECT(A'→ε)={d,#}

SELECT(B→dB')={e}

SELECT(B'→bB')={b}

SELECT(B'→ε)={e}

(3)S→Aa|b

　A→SB

　B→ab

消除左递归:

S→Aa|b→SBa|b→bS'

S'→BaS'|ε

B→ab

FIRST集:

 FIRST(S)→{b}

FIRST(S')→{a,ε}

FIRST(B)→{a}

FOLLOW集:

FOLLOW(S)→{#}

FOLLOW(S')→{#}

FOLLOW(B)→{a}

SELECT(S→bS')={b}

SELECT(S'→BaS')={a}

SELECT(S'→ε)={#}

SELECT(B→ab)={a}

课堂练习：

求以下文法的FIRST集、FOLLOW集和SELECT集。

(1)S→Ap

A→a|ε

A→cA

A→aA

FIRST集:

FIRST(Ap)→{a,c,p}

FIRST(a)→{a}

FIRST(ε)→{ε}

FIRST(cA)→{c}

FIRST(aA)→{a}

FOLLOW集:

FOLLOW(S)→{#}

FOLLOW(A)→{p}

SELECT集：

SELECT(S→Ap)={a,c,p}

SELECT(A→a)={a}

SELECT(A→ε)={p}

SELECT(A→cA)={c}

SELECT(A→aA)={a}

(2)S->Ap
S->Bq
A->a
A->cA
B->b
B->dB

FIRST集:

FIRST(a)→{a}

FIRST(b)→{b}

FIRST(cA)→{c}

FIRST(dB)→{d}

FIRST(Bq)→{b,d}

FIRST(Ap)→{a,c}

FOLLOW集:

FOLLOW(S)→{#}

FOLLOW(A)→{p}

FOLLOW(B)→{q}

SELECT集：

SELECT(S->Ap)={a,c}

SELECT(S->Bq)={b,d}

SELECT(A->a)={a}

SELECT(A->cA)={c}

SELECT(B->b)={b}

SELECT(B->dB)={d}