机器学习（3）之KNN算法

@

目录

• 算法原理
  • 算法步骤
  • KNN三要素
  • KNN算法实现方式
    • KD Tree的构建
    • KD tree查找最近邻

算法原理

• K近邻(K-nearst neighbors, KNN)是一种基本的机器学习算法，所谓k近邻，就是k个最近的邻居的意思，说的是每个样本都可以用它最接近的k个邻居来代表。
• KNN在做回归和分类的主要区别在于最后做预测的时候的决策方式不同。KNN在分类预测时，一般采用多数表决法；而在做回归预测时，一般采用平均值法。

算法步骤

1. 从训练集合中获取K个离待预测样本距离最近的样本数据；
2. 根据获取得到的K个样本数据来预测当前待预测样本的目标属性值。

KNN三要素

1. K值的选择：对于K值的选择，一般根据样本分布选择一个较小的值，然后通过交叉验证来选择一个比较合适的最终值；当选择比较小的K值的时候，表示使用较小领域中的样本进行预测，训练误差会减小，但是会导致模型变得复杂，容易过拟合；当选择较大的K值的时候，表示使用较大领域中的样本进行预测，训练误差会增大，同时会使模型变得简单，容易导致欠拟合；
2. 距离的度量：一般使用欧氏距离(欧几里得距离)；
3. 决策规则：在分类模型中，主要使用多数表决法或者加权多数表决法；在回归模型中，主要使用平均值法或者加权平均值法。

KNN算法实现方式

1. 蛮力实现(brute)：计算预测样本到所有训练集样本的距离，然后选择最小的k个距离即可得到K个最邻近点。缺点在于当特征数比较多、样本数比较多的时候，算法的执行效率比较低;
2. KD树(kd_tree)：KD树算法中，首先是对训练数据进行建模，构建KD树，然后再根据建好的模型来获取邻近样本数据。

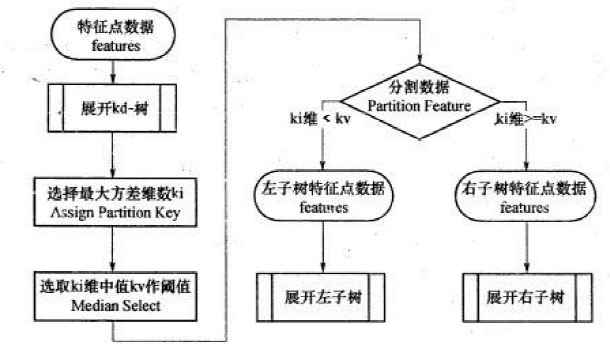
KD Tree的构建

KD树采用从m个样本的n维特征中，分别计算n个特征取值的方差，用方差最大
的第k维特征n_k作为根节点。对于这个特征，选择取值的中位数n_kv作为样本的划分点，对于小于该值的样本划分到左子树，对于大于等于该值的样本划分到右子树，对左右子树采用同样的方式找方差最大的特征作为根节点，递归即可产生KD树。

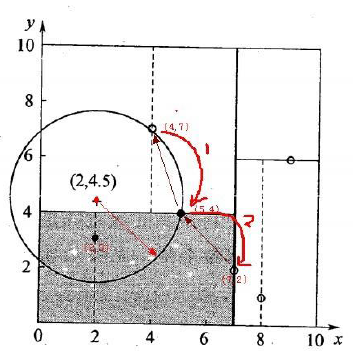
KD tree查找最近邻

当我们生成KD树以后，就可以去预测测试集里面的样本目标点了。对于一个目标点，我们首先在KD树里面找到包含目标点的叶子节点。以目标点为圆心，以目标点到叶子节点样本实例的距离为半径，得到一个超球体，最近邻的点一定在这个超球体内部。然后返回叶子节点的父节点，检查另一个子节点包含的超矩形体是否和超球体相交，如果相交就到这个子节点寻找是否有更加近的近邻,有的话就更新最近邻。如果不相交那就简单了，我们直接返回父节点的父节点，在另一个子树继续搜索最近邻。当回溯到根节点时，算法结束，此时保存的最近邻节点就是最终的最近邻。