欧拉回路心得

对于欧拉回路为什么一定要用栈，偶进行了一下小小的探究（感谢崔学长的数据）。

样例如图所示：

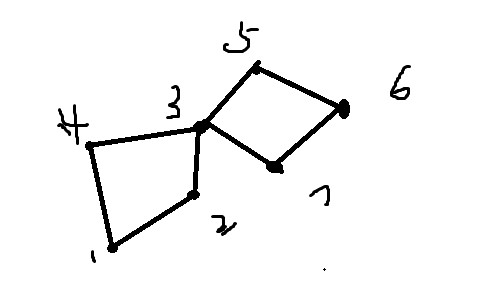
 不用栈，直接输出会怎样呢？

void euler(int u){
    for(int v=1; v<=n; v++){
        if(G[u][v]){
            G[u][v]--;
            G[v][u]--;
            printf("%d %d\n", u, v);
            euler(v);
        }
    }
}

输出结果如下：

一开始输出路径会是1->2->3->4->1，搜完这些，会从3开始继续搜索并输出，3->5->6->7->3。很明显，这是错误的。、

那么用栈呢？

void euler(int u){
    for(int v=1; v<=n; v++){
        if(G[u][v]){
            G[u][v]--;
            G[v][u]--;
            euler(v);
            S.push(node(u, v));
        }
    }
}

 在main函数里添加：

while(!S.empty()){
    node e = S.top(); S.pop();
    printf("%d %d\n", e.x, e.y);
}

结果如下：

假设当前走到了3结点，那么下一个应当是4，然后是1，接着的操作是将4->1,3->4入栈，进行完这些操作，会继续搜索3->5->6->7->3，接着把7->3, 6->7, 5->6, 3->5,2->3, 1->2入栈.

依次将这些边弹出会如何？如上图结果显示。

懂了这些，便可将上面代码修改下：

void euler(int u){
    for(int v=1; v<=n; v++){
        if(G[u][v]){
            G[u][v]--;
            G[v][u]--;
            euler(v);
            printf("%d %d\n", v, u)
        }
    }
}

测试样例：

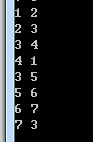
7 8
1 2
2 3
3 4
4 1
3 5
5 6
6 7
7 3

下面给出完全的用栈保存路径的代码：

#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <queue>
#include <stack>
using namespace std;

const int maxn = 50+20;

int G[maxn][maxn], n;

struct node{
    int x, y;
    node(int x, int y):x(x), y(y) {}
};

stack<node> S;

void euler(int u){
    for(int v=1; v<=n; v++){
        if(G[u][v]){
            G[u][v]--;
            G[v][u]--;
            euler(v);
            S.push(node(u, v));
        }
    }
}

int main(){
    int m;
    memset(G, 0, sizeof(G));
    scanf("%d%d", &n, &m);
    for(int i=0; i<m; i++){
        int u, v;
        scanf("%d%d", &u, &v);
        G[u][v] = G[v][u] = 1;
    }

    euler(1);

    while(!S.empty()){
        node e = S.top(); S.pop();
        printf("%d %d\n", e.x, e.y);
    }

    return 0;
}