Pytorch 激活函数

学习过程知识粗略记录，用于个人理解和日后查看

包导入

import torch
from torch import nn
from torch import autograd
import numpy as np

Sinmoid

非线性函数：f(x)=σ(x)=1/(1+e^(-x))
缺点： 梯度消失、输出不是0的均值、涉及除法，反向传播求误差的时候计算量大

'''output->[0,1]'''
m=nn.Sigmoid()
input=autograd.Variable(torch.randn(2))
print(input)
print(m(input))

output

Tanh

• 双曲三角函数：f(x)=tanh(x)=(e^x-e(-x))/(e^x+e(-x))
• Sinmoid通过简单变换后得到：tanh(x)=2σ(2x)-1
• 缺点： 梯度消失

'''out->[-1,1]'''
m=nn.Tanh()
input=autograd.Variable(torch.randn(2))
print(input)
print(m(input))

output

Hard Tanh

• 通过给定的阈值直接得到最终结果
• f(x)=a,x>a; f(x)=b,x<b; f(x)=x,其他
• eg.f=Hardtanh(-2,2):所有大于2的输入变成2，所有小于-2的输入变成-2，其他的保持不变

m=nn.Hardtanh(-2,2)
input=autograd.Variable(torch.randn(10))
print(input)
print(m(input))

output

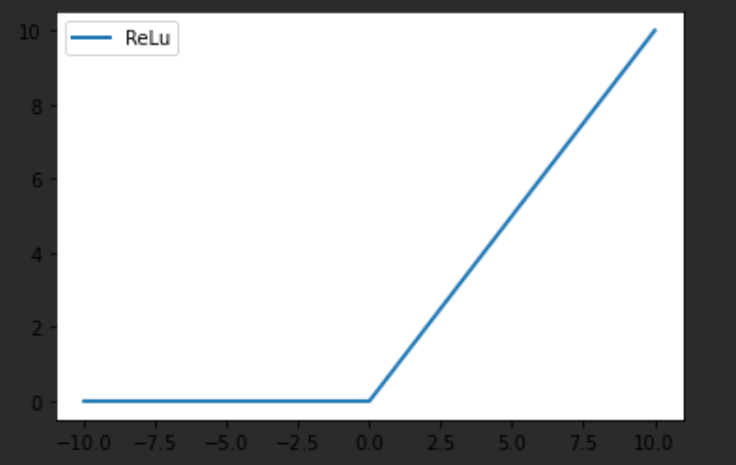
ReLU

• 线性整流函数，分段函数
• eg.f(x)=max(0,x)：f(x)=x,x>0; f(x)=0,x<0
• 优点：简单，只需要一个阈值就可以计算结果；在随机梯度下降的训练中收敛会更快，究其原因是因为ReLU是非饱和的

m=nn.ReLU()
input=autograd.Variable(torch.randn(5))
print(input)
print(m(input))

output

ReLU拓展

# Leaky ReLU：x<0 f(x)=ax (a一般为1e-2),其他不变
input=autograd.Variable(torch.randn(5))
m=nn.LeakyReLU(negative_slope=1e-2,inplace=True)# negative_slope->a
print(input,"
->LeakyReLU:",m(input))

# PReLU:f(x)=max(0,x)+α*min(0,x)
input=autograd.Variable(torch.randn(5))
m=nn.PReLU(num_parameters=1)# num_parameters->α=>int
print(input,"
->PReLU:",m(input))

# RReLU:Leaky ReLU的随机版本，即参数a随机产生
input=autograd.Variable(torch.randn(5))
m=nn.RReLU(1e-4,1e-1,inplace=True)
print(input,"
->RReLU:",m(input))

# ELU: ELU(a)(z)=a(exp(z)-1), z<0;z, z>0
input=autograd.Variable(torch.randn(5))
m=nn.ELU(alpha=1e-2,inplace=True)
print(input,"
->ELU:",m(input))

output

Softmax

• 归一化指数函数 Sinmoid Plus
• 将每个元素压缩到(0,1),且所有元素之和为1
• fi(x)=exp(xi)/∑j exp(xj)
• 传入dim参数，二维下，dim=0，列方向上和为1，dim=1，行方向上和为1

m=nn.Softmax(dim=0)
input=autograd.Variable(torch.randn(2,5))
print(input)
print(m(input))

output

LogSoftmax

• 应用于softmax函数前的对输入应用对数的函数
• fi(x)=log(exp(xi)/∑j exp(xj))
• 用法和Softmax相同

m=nn.LogSoftmax(dim=0)
input=autograd.Variable(torch.randn(2,5))
print(input)
print(m(input))

如有错误，欢迎指正

同时发布在CSDN中：https://blog.csdn.net/tangkcc/article/details/119785845