你知道pytorch的backward求导的要求吗?你想了解pytorch反向传播的原理吗?本文将记录不同结果对求导参数的要求,并使用代码详细说明,本文借鉴它人博客对pytorch反向传播原理进行解释。
backward函数解释 :
一. 如果是标量对向量求导(scalar对tensor求导),那么就可以保证上面的计算图的根节点只有一个,此时不用引入grad_tensors参数(即梯度权重),直接调用backward函数即可。
代码如下:
x = torch.ones(2, requires_grad=True) # x = [1,1]
y = 2 * x[0] ** 3+ 2 * x[1] ** 3 # y=2*x^2 ,其中 x = [1,1], y是2维
y.backward() # y'= ∂(2*x^2)/∂x = 4x
print(x.grad) # x在x=[1,1]时候的 导数值
结果如下:
二. 如果是(向量)矩阵对(向量)矩阵求导(tensor对tensor求导),实际上是先求出矩阵中每一个元素的梯度值(每一个元素的梯度值的求解过程对应下面的计算图的求解方法), 然后将这个矩阵与grad_tensors参数(即梯度权重)对应的矩阵进行对应的点乘,得到最终的结果。
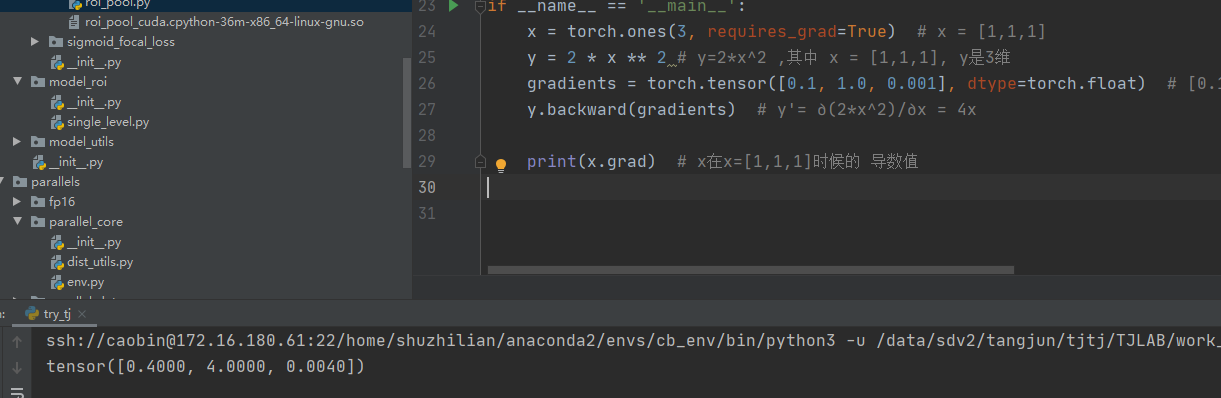
x = torch.ones(3, requires_grad=True) # x = [1,1,1]
y = 2 * x ** 2 # y=2*x^2 ,其中 x = [1,1,1], y是3维
gradients = torch.tensor([0.1, 1.0, 0.001], dtype=torch.float) # [0.1, 1.0, 0.0001] 表示各个维度上导函数前的权重
y.backward(gradients) # y'= ∂(2*x^2)/∂x = 4x
print(x.grad) # x在x=[1,1,1]时候的 导数值
结果如下:
三.如果是(向量)矩阵对(向量)矩阵求导(tensor对tensor求导),无gradients就会报错。
x = torch.ones(3, requires_grad=True) # x = [1,1,1]
y = 2 * x ** 2 # y=2*x^2 ,其中 x = [1,1,1], y是3维
gradients = torch.tensor([0.1, 1.0, 0.001], dtype=torch.float) # [0.1, 1.0, 0.0001] 表示各个维度上导函数前的权重
y.backward() # y'= ∂(2*x^2)/∂x = 4x
print(x.grad) # x在x=[1,1,1]时候的 导数值
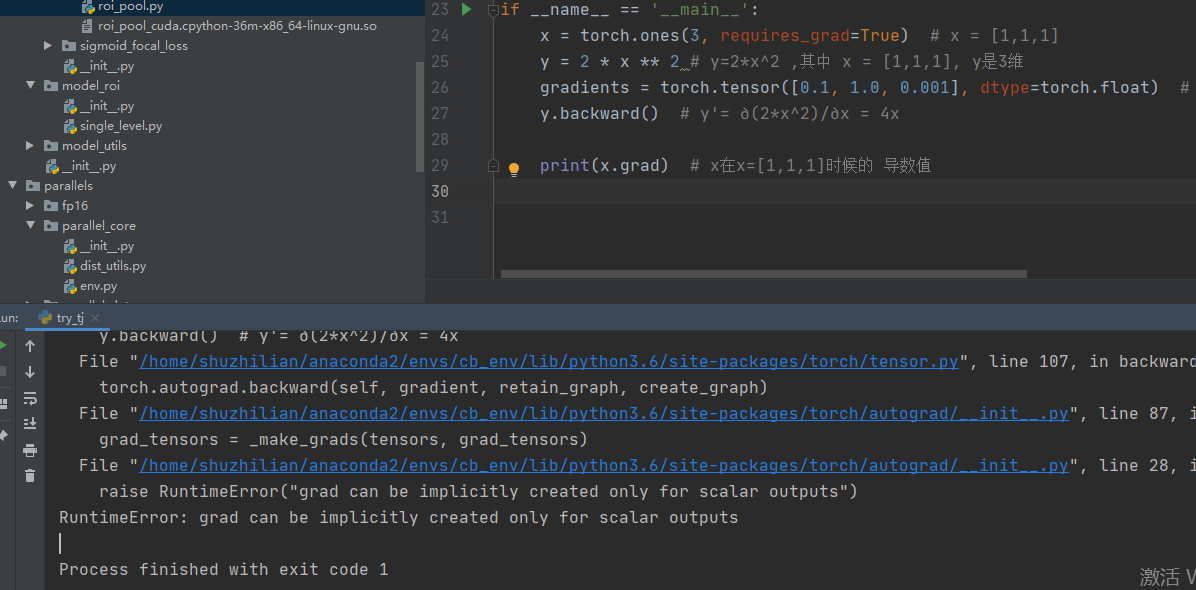
结论: 反向传播必须要各个节点的权重,因标量只有一个值,故而无需权重,而矩阵是一个向量,故而需要对应的权重。
四.backward结合Fuction函数使用方法(红色字体很重要):
class MyReLU(torch.autograd.Function):
def forward(self, input_):
# 在forward中,需要定义MyReLU这个运算的forward计算过程
# 同时可以保存任何在后向传播中需要使用的变量值
self.save_for_backward(input_) # 将输入保存起来,在backward时使用
output = input_.clamp(min=0) # relu就是截断负数,让所有负数等于0
return output
def backward(self, grad_output):
# 根据BP算法的推导(链式法则),dloss / dx = (dloss / doutput) * (doutput / dx)
# dloss / doutput就是输入的参数grad_output、
# 因此只需求relu的导数,在乘以grad_outpu
input_, = self.saved_tensors
grad_input = grad_output.clone()
grad_input[input < 0] = 0 # 上述计算的结果就是左式。即ReLU在反向传播中可以看做一个通道选择函数,所有未达到阈值(激活值<0)的单元的梯度都为0
return grad_input
在结合官网列子理解:
>>> class Exp(Function):
>>>
>>> @staticmethod
>>> def forward(ctx, i):
>>> result = i.exp()
>>> ctx.save_for_backward(result) # 保留e^x
>>> return result
>>>
>>> @staticmethod
>>> def backward(ctx, grad_output):
>>> result, = ctx.saved_tensors
>>> return grad_output * result # 恰好(dloss/dout)*e^x
>>>
>>> #Use it by calling the apply method:
>>> output = Exp.apply(input)
这里首先还是放出backward( )函数的pytorch文档,因为整个说明主要还是围绕这个函数来进行的。

问题描述
从上面的文档可以看到backward函数有一个奇怪的参数:grad_tensors,在实现pytorch的官方教程中可以发现:
import torch
import torch.nn as nn
x = torch.tensor([2, 3, 4], dtype=torch.float, requires_grad=True)
print(x)
y = x * 2
while y.norm() < 1000:
y = y * 2
print(y)
y.backward(torch.ones_like(y))
print(x.grad)
上面的程序的输出为:
tensor([2., 3., 4.], requires_grad=True)
tensor([ 512., 768., 1024.], grad_fn=<MulBackward0>)
tensor([256., 256., 256.])
- 1
- 2
- 3
这里我们分布来讲述上面的过程:
- 创建一个张量x,并设置其 requires_grad参数为True,程序将会追踪所有对于该张量的操作,当完成计算后通过调用
.backward(),自动计算所有的梯度, 这个张量的所有梯度将会自动积累到.grad属性。 - 创建一个关于x的函数y,由于x的requires_grad参数为True,所以y对应的用于求导的参数
grad_fn为<MulBackward0>。这是因为在自动梯度计算中还有另外一个重要的类Function,Tensor和Function互相连接并生成一个非循环图,它表示和存储了完整的计算历史。 每个张量都有一个.grad_fn属性,这个属性引用了一个创建了Tensor的Function(除非这个张量是用户手动创建的,即,这个张量的grad_fn是None,例如1中创建的x的grad_fn是None) - 我们进行反向传播并输出x的梯度值,而这里出现了一个参数
torch.ones_like(y)即为grad_tensors参数,这里便引入了我们的问题:
为什么在求导的过程中需要引入这个参数,如果我们不引入这个参数的话,则会报下面的错误:
RuntimeError: grad can be implicitly created only for scalar outputs
即为提示我们输出不是一个标量
下面就开始分析这个问题以及这个参数的作用。
pytorch实现反向传播中求导的方法
这里主要参考pytorch计算图文章中的讲解:
由上面的文章知道pytorch是动态图机制,在训练模型时候,每迭代一次都会构建一个新的计算图。而计算图其实就是代表程序中变量之间的关系。对于y = ( a + b ) ( b + c ) y=(a+b)(b+c)y=(a+b)(b+c)这个例子可以构建如下计算图:
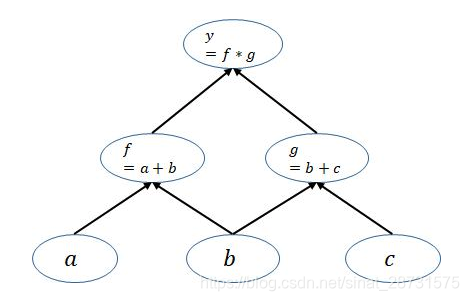
上面的计算图中每一个叶子节点都是一个用户自己创建的变量,在网络backward时候,需要用链式求导法则求出网络最后输出的梯度,然后再对网络进行优化,如下就是网络的求导过程。
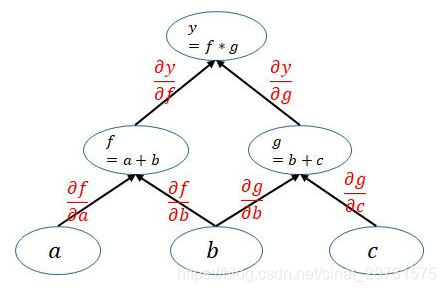
通过观察上面的计算图可以发现一个很重要的点:
pytorch在利用计算图求导的过程中根节点都是一个标量,即一个数。当根节点即函数的因变量为一个向量的时候,会构建多个计算图对该向量中的每一个元素分别进行求导,这也就引出了下一节的内容
这里顺带说一下:
pytoch构建的计算图是动态图,为了节约内存,所以每次一轮迭代完也即是进行了一次backward函数计算之后计算图就被在内存释放,因此如果你需要多次backward只需要在第一次反向传播时候添加一个retain_graph=True标识,让计算图不被立即释放。实际上文档中retain_graph和create_graph两个参数作用相同,因为前者是保持计算图不释放,而后者是创建计算图,因此如果我们不想要计算图释放掉,将任意一个参数设置为True都行。(这一段说明的内容与本文主要说明的内容无关,只是顺带说明一下)
参考博客:https://blog.csdn.net/sinat_28731575/article/details/90342082