数组的一些应用场景

今天主要回顾一下数组方面的知识吧，有一维数组，二维数组，以及它们的经典应用。、

昨天一维数组的一些注意：

int[] arr = new int[]{5, 3, 7, 1, 8, 9, 2}; 

表示定义了一个元素类型为整型的数组，数组中的元素是 5，3，7，1，8，9，2，意味着数组的长度是 7。

数据类型[] 数组名 = {元素1，元素2，元素3，……}；---不允许分开定义

 

数组的应用

1.操作指定位置上的元素：数组名[下标] 

2.获取数组长度：数组名.length;

3.遍历数组，

（1）for(int i = 0; i < arr.length; i++){
            System.out.println(arr[i]);
        }   //与其说遍历数组不如说遍历下标
 
（2）for(int i : arr){
            //arr[i] += 10;                    //只能遍历数组但是不能改变数组中的值
            System.out.println(i);
        }  //增强 for 循环，此时的 i 依次表示数组中的每一个元素

　　

4.获取数组中最值（最大值/最小值）

方式一：定义变量来记录数组中的最大值，然后遍历数组，让数组中的元素依次与最大值进行比较；如果大于最大值，则将这个元素覆盖原来的最大值

方式二：定义变量来记录最大值的下标。

 

//4.获取数组中最值（最大值/最小值）
		//方式一：定义变量来记录数组中的最大值，然后遍历数组，让数组中的元素依次与最大值进行比较；如果大于最大值，则将这个元素覆盖原来的最大值
		int max = arr[0];
		for(int i : arr){
			if(max < i){
				max = i;
			}
		}
		System.out.println(max);
		//方式二：定义变量来记录最大值的下标。
		int flag = 0;
		for(int i = 1; i < arr.length; i++){
			if(arr[flag] < arr[i]){
				flag = i;
			}
		}
		System.out.println(arr[flag]);

　　

5.数组的排序

 

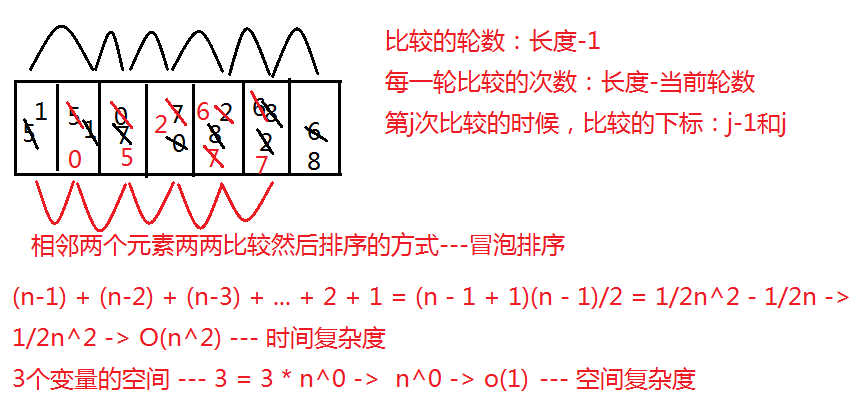
(n-1)+(n-2)+(n-3)+……+2+1 = (n-1+1)(n-1)/2 = 1/2 n^2 - 1/2 n  ->  1/2 n^2  -> O(n^2)

时间复杂度：在程序中找一段必然会执行的代码，将这段代码的执行时间认为是单位1，执行这个单位 1 需要的次数就是时间复杂度 -

时间复杂度不考虑系数，一般来说是找最高阶 -> O(n^x)，O((logn)^x),O(n^x(logn)^y)    （决定的是效率，快慢程度）

空间复杂度：这段程序执行所需要额外耗费的空间就是空间复杂度

3个变量的空间 --- 3 = 3 * n^0 -> n^0 ->O(1)  (占用的内存)

//冒泡排序
		for(int i = 1; i < arr.length; i++){
			//定义一个循环控制每一轮比较的次数
			for(int j =1; j <= arr.length - i; j++){
				if(arr[j -1] > arr[j]){
					int temp = arr[j - 1];
					arr[j - 1] = arr[j];
					arr[j] = temp;
				}
			}
		}
		String str = Arrays.toString(arr);
		System.out.println(str);

 

就像是打擂台，摁住第一个不放跟后面的比较，下一步拿第二个跟后面的比较。（遇到小的就换掉）

5 1 7 0 8 2 6        比较的轮数：长度 - 1

                            每一轮选定的下标：轮数 - 1

                            每一轮比较的下标：轮数 ->最后一位

选定一位依次和其他位比较并排序 --- 选择排序

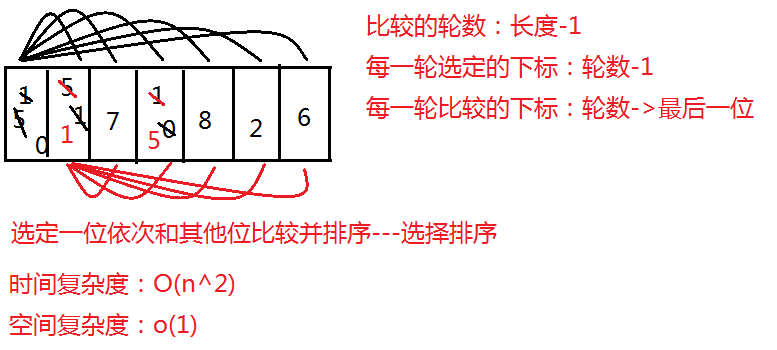
时间复杂度：O(n^2)  ->(n-2)+(n-3)+……+2+1 = (n-1)(n-2)/2=1/2 n^2+1/2 n -> O(n^2)

空间复杂度：O(1)

//选择排序
		//控制轮数
		for(int i = 1; i < arr.length; i++){
			//控制每一轮要比较的下标
			for(int j = i; j < arr.length; j++){
				if(arr[i - 1] > arr[j]){
					int temp = arr[i - 1];
					arr[i - 1] = arr[j];
					arr[j] = temp;
				}
			}
		}
		//只能进行升序排序
		//扩展：底层用的是快速排序 + 归并排序
		//时间复杂度：O(nlogn)
		Arrays.sort(arr);
		System.out.println(Arrays.toString(arr));

　　

 扩展：冒泡排序和选择排序都是稳定的排序算法  --- 排序算法的稳定与否的依据是相等的元素在排序的时候是否需要交换

 

6.反转数组：首尾互换 --- 时间复杂度O(n)，空间复杂度O(1)

//反转数组
		//方式一：
		//时间复杂度：O(n)，空间复杂度：O(n)
		int[] newArr = new int[arr.length];
		for(int i = arr.length - 1, j = 0; i >= 0; i--,j++){
			newArr[j] = arr[i];
		}
		System.out.println(Arrays.toString(newArr));
		//方式二：头尾交换
		//时间复杂度：O(n)，空间复杂度 O(1)
		for(int i = 0, j = arr.length - 1; i <= j; i++, j--){
			int temp = arr[i];
			arr[i] = arr[j];
			arr[j] = temp;
		}
		System.out.println(Arrays.toString(arr));

　　

7.数组元素的查找：

数组元素无序的前提下，获取一个元素的位置只能通过遍历的方式一一比较。（一个一个的找）

如果数组元素有序，使用二分查找 --- 空间复杂度 O(1)，时间复杂度 O(logn)。

   (1/2)x = n ->x = log1/2n = log2n/log21/2   ->log2n  ->logn(默认底数为n)（每次折损 x 次，）

    2x = n ->x = log2n  ->logn(默认底数为n)

i

2  5  7  8  9  12  35  56  75  76  80   87  352

min                   mid                               max

           mid        max

 

arr[mid] ==i --- mid             arr[mid] > i           arr[mid] < i

 

8.数组的复制

System.arraycopy(要复制的数组，要复制的起始下标，存放的数组，要存放的起始下标，个数);

Arrays.copyOf(要扩容的数组, 扩容的大小);    //用数组的复制可以实现数组的扩容

/数组的复制
		//表示从 arr1 下标为 2 的位置上复制 4 个元素放入 arr2 数组中，
		//从 arr2 数组的下标为 4 的位置存放
		int[] arr1 = {5,1,7,0,8,2,6};
		int[] arr2 = new int[5];
		System.arraycopy(arr1,2,arr2,0,4);
		System.out.println(Arrays.toString(arr2));
		
		//数组的扩容 --- 数组的复制 --- 产生一个新的数组，导致扩容之后的数组和原数组不是同一个
		int[] arr = {3,6,1,7,9};
		int[] newArr = new int[8];
		System.arraycopy(arr,0,newArr,0,arr.length);
		arr = newArr;
		
		arr = Arrays.copyOf(arr,8);//这一步等价于前面三步
		System.out.println(Arrays.toString(arr));

　　

二维数组

存储的元素是一维数组  ---  存储数组的数组（就像是一个大盒子里面有很多的小盒子）

    定义格式

数据类型[][]  数组名 = new  数据类型[包含的一维数组的个数][每一个一维数组的长度];

int[ ][ ] arr = new int[3][5]; 表示定义了一个能存储 3 个整型一维数组，每一个一维数组有 5 个整型元素

数据类型[ ][ ]  数组名 = new  数据类型[包含的一维数组的个数][];

int[ ][ ]  arr = new int[5][ ];  定义了一个能存储 5 个整型一维数组的二维数组 --- 必须先保证这一位上的一维数组先给定大小，再给值

 

数据类型[ ][ ] 数组名 = {{数组1}, {数组2}, {数组3},…};

int[ ][ ] arr = {{2,4,1},{4,7,2,9},{3},{5,0,6,7,4,3}};  --- 二维数组的大小为 4

注意：[ ]如果在变量名之前那么紧跟着数据类型，也就意味着后面定义的变量是这个类型

数组的内存

练习：杨辉三角

1

1 1

1 2 1

1 3 3 1

1 4 6 4 1

特点：每一行的开始和结束都是1；其余位置的元素是计算：arr[i][j] = arr[i - 1][j] + arr[i - 1][j - 1];

输入一个数字表示行数，输出对应的前 n 行。

import java.util.Scanner;
import java.util.Arrays;
public class Demo{
	public static void main(String[] args){
		Scanner s = new Scanner(System.in);
		//定义行数
		int n = s.nextInt();
		//定义二维数组来存储杨辉三角
		int[][] arr = new int[n][];
		//遍历数组，向里填充元素
		for(int i = 0; i < n; i++){
			//先给每一个一维数组定义大小
			arr[i] = new int[i + 1];
			//遍历一个一维数组，向里填充元素
			for(int j = 0; j <= i; j++){
				//判断头尾元素
				if(j == 0 || j ==i){
					arr[i][j] = 1;
				}else{
					arr[i][j] = arr[i - 1][j] + arr[i - 1][j - 1];
				}
				//填充完成之后打印这个填充的元素
				System.out.print(arr[i][j]+"	");
			}
			System.out.println();
		}
		
		//一个循环打印九九乘法表
		for(int i = 1,j = 1;i <= 9; j++){
			//无论哪一行，上来都是先打印*
			System.out.print("*");
			//判断是否打印完最后一个*
			if(j == i){
				//换行
				System.out.println();
				//行数 +1
				i++;
				// *从头开始计数
				j = 0;
			}
		}
	}
}