问题的引出
给定一个函数(f),以及一堆约束函数(g_1,g_2,...,g_m)和(h_1,h_2,...,h_l).带约束的优化问题可以表示为
下面我们将来讨论具有上述问题的解,一共可以分为四种情况:
- 无约束条件
- 只有等式约束条件
- 只有不等式约束条件
- 同时有等式和不等式约束条件
无约束条件
我们先来复习一下多元函数取得极值的条件。设(f: R^n o R),是一个连续可导的函数,并且(J_f)和(H_f)分别是(f)的一阶梯度和二阶梯度矩阵(Hession矩阵),判断(f(x^*))是它的一个极值的条件是:
- (J_f=0,H_f)是负定矩阵,则(x^*)是(f)的极大值
- (J_f=0,H_f)是正定矩阵,则(x^*)是(f)的极小值
- (J_f=0,H_f)是半正定或半负定或不定矩阵,则需要进一步讨论
这样,无约束下的最优化问题可以通过上述规则来求函数的极值。
等式约束条件
只含等式约束条件的最优化问题表示为(以一个等式约束为例)
下面用具体的实例来讨论这一类问题,令
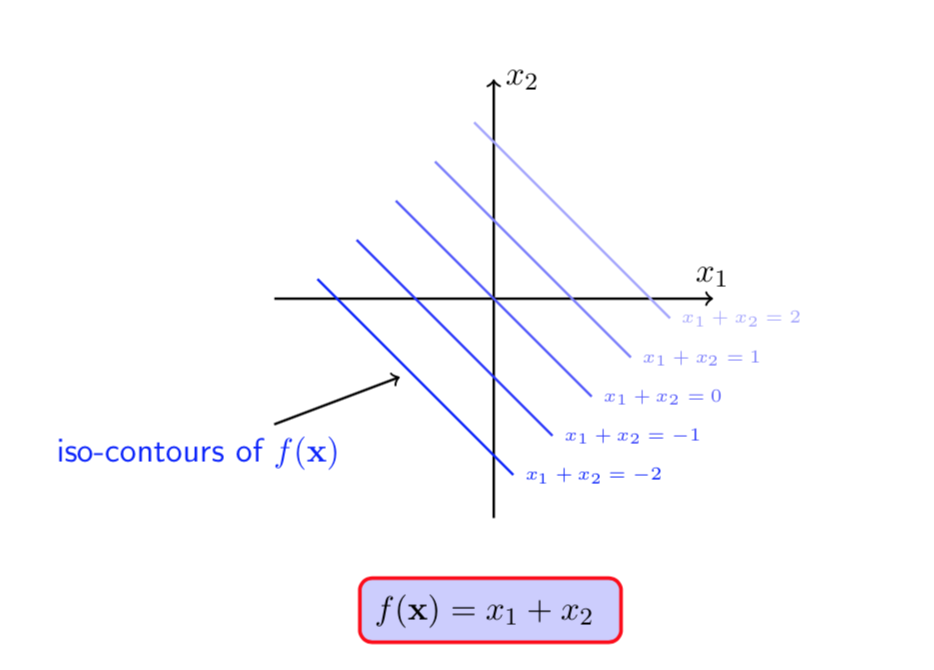
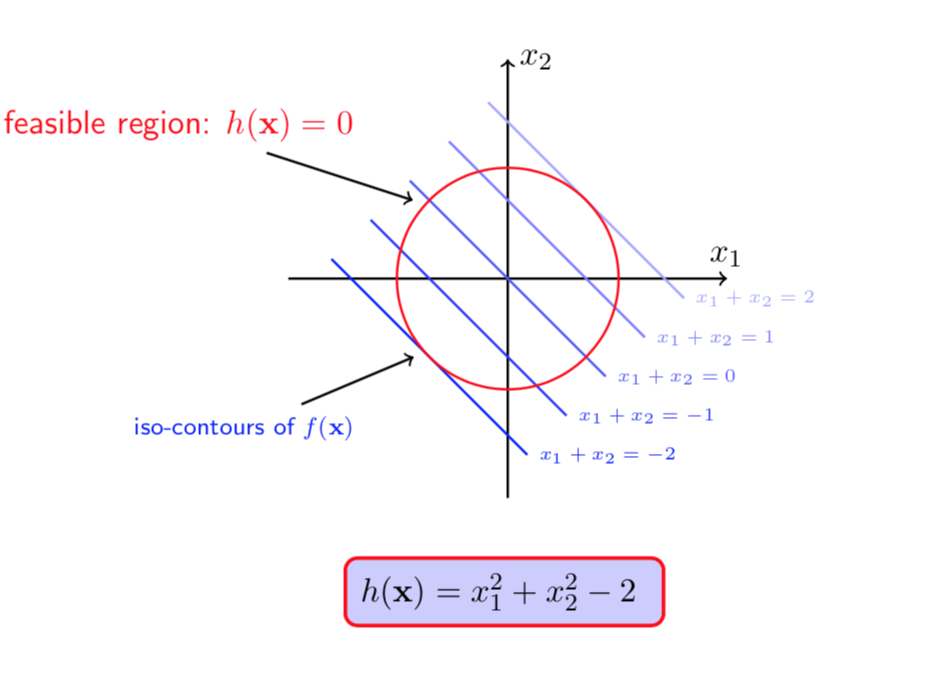
图(1 ) 图(2)
在图(1)和(2)中蓝色线是(f(X))的等高线,红色线是在(h(X) = 0)约束下的可行域((X)可取值的可行范围)。
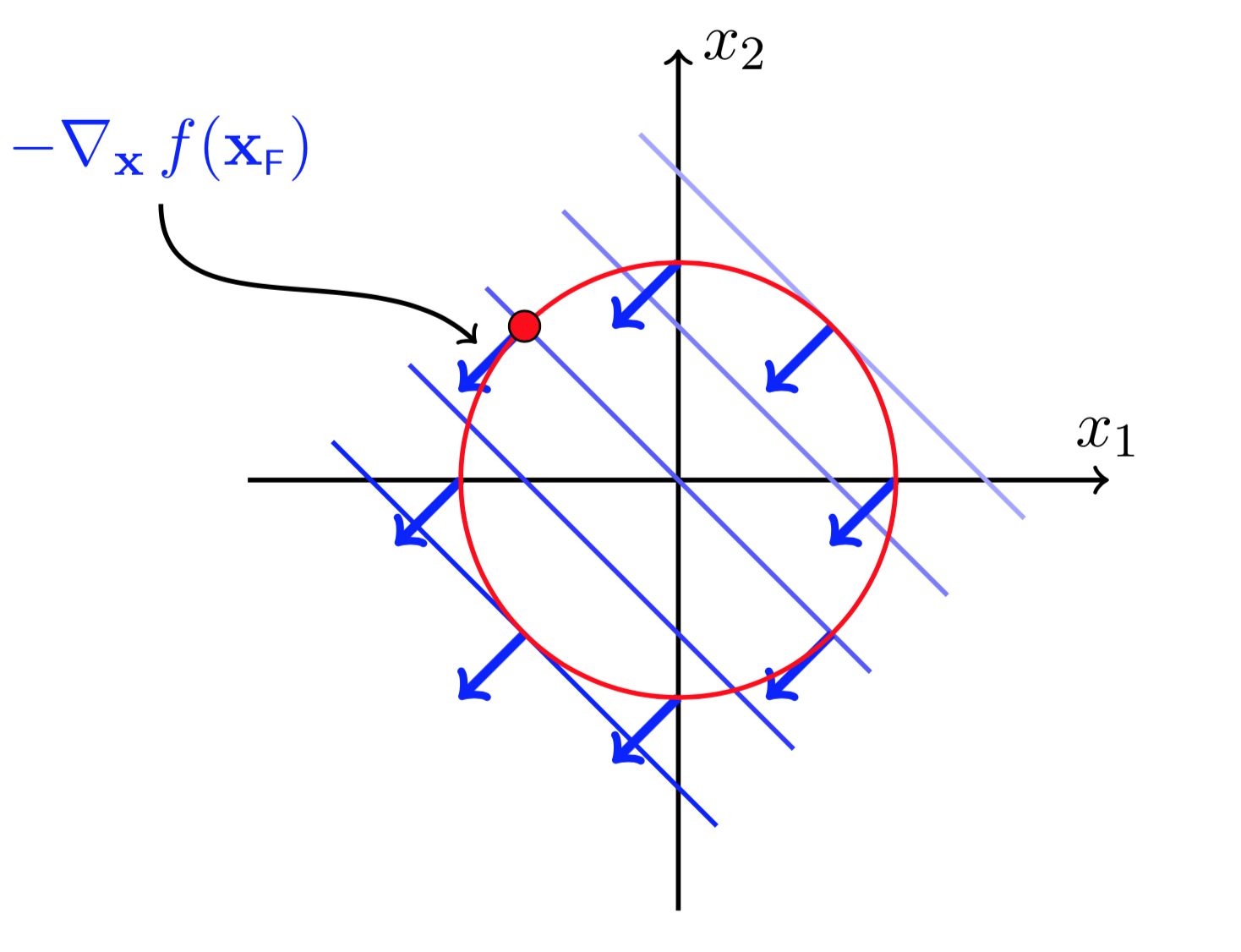
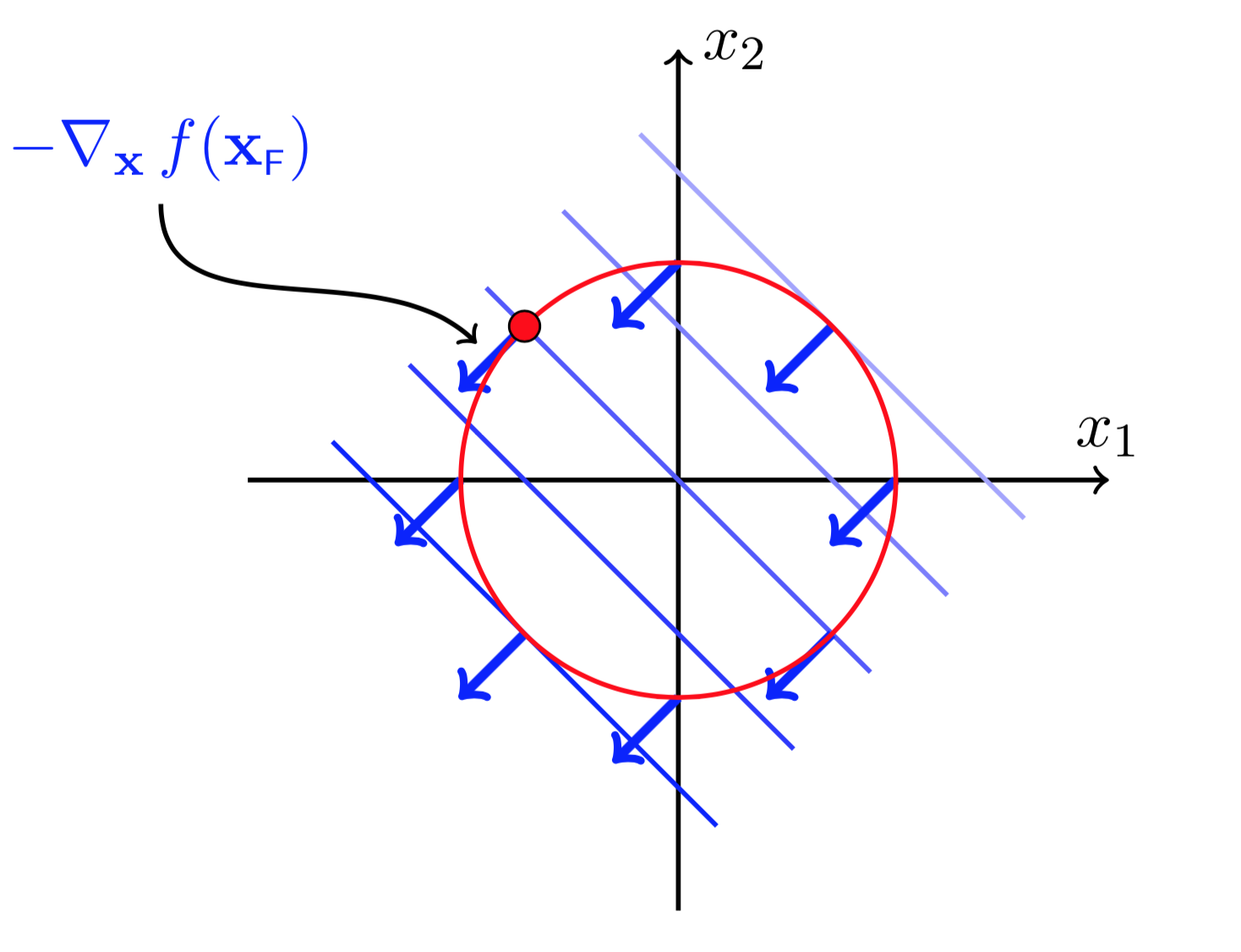
图(3 ) 图(4)
为了找到(f(X))的最小值。如图(3),我们需要从红色点的位置(点(X_F))往某一个方向走一小步,并且目标位置依然在可行域内(满足(h(X)=0)的限制),同时还希望(f(X))的值能够下降,即
我们知道沿着梯度的反方向是下降最快的。如果要满足(quad f(X_F) >f(X_F+ Delta X))则必须有
意思就是说,下一步走的方向(Delta X)应该与(- abla_Xf(X))的夹角小于等于90度。
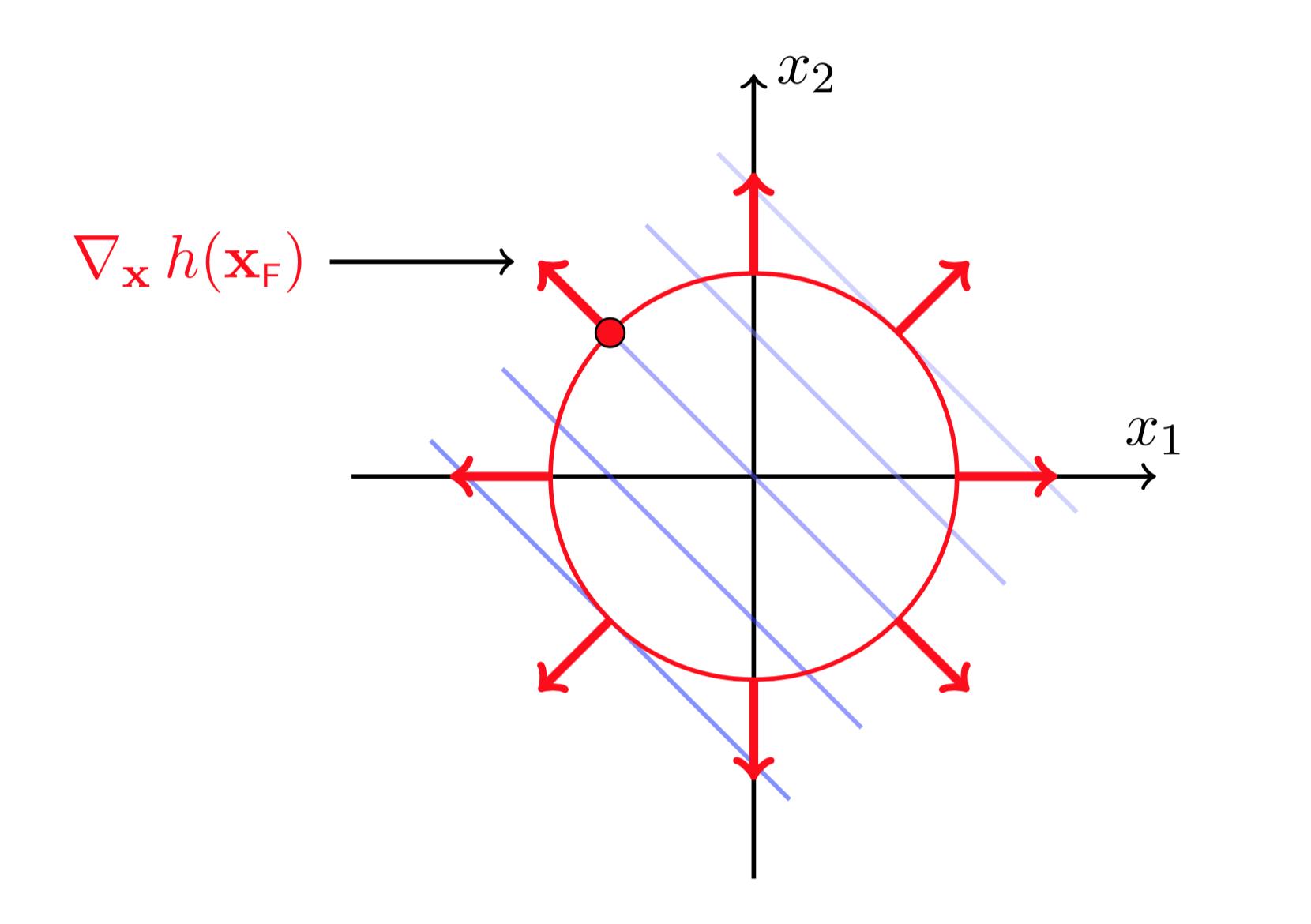
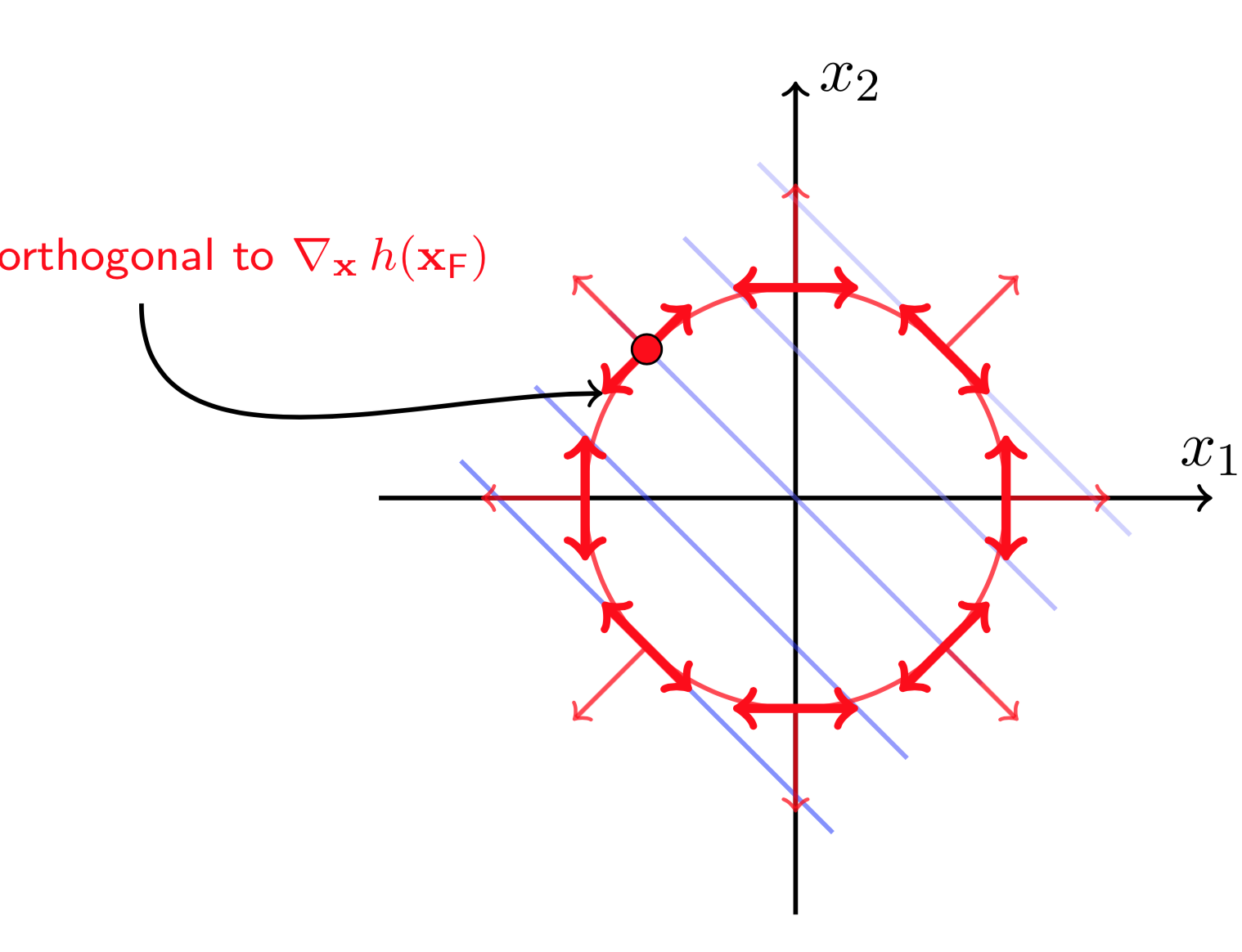
图(5 ) 图(6)
图(5)和图(6)分别画出了约束函数(h(X))的梯度方向以及梯度的正交方向。为了限制在移动(X_F)后,使得(X_F+Delta X)依然在约束曲线上,则(Delta X)必须沿着(h(X))梯度的正交方向移动(否则(h(X))会增大或减小,这样不再满足约束条件(h(X)= 0))。这说明任何时刻都有
-
(Delta X)沿着( abla_Xh(X_F))正交方向移动,可以保证(h(X_F+Delta X)=0).
-
当$f(X_F) >f(X_F+ Delta X) $时,必须有
[Delta X cdot (- abla_X f(X)) > 0 ]
考虑一种情况
其中(mu)是一个常数,此时
- 当移动(Delta X)时,(Delta X cdot (- abla_x f(X)) = -muDelta X cdot abla_x h(X) = 0).
- 无法找到一个方向(Delta X)使得(f(X))能够继续减小或增大,此时(X_F)是函数的一个极值点.
回到我们最初的问题
定义拉格朗日函数
(X^*)是一个局部最小值的充分条件是
- ( abla _XL(X^*,mu^*) = 0).
- ( abla _{mu}L(X^*,mu^*) = 0).
- (Y^T abla_{XX}^2L(X^*,mu^*)Y>0 quad s.t. ;( abla_Xh(X^*))^TY = 0)
最后的约束条件是保证(Y)的方向与(h(X))梯度方向正交。上面结论很容易推广到多等式约束问题,设
定义拉格朗日函数
(X^*)是一个局部最小值的充分条件是
- ( abla _XL(X^*,mu^*) = 0).
- ( abla _{mu}L(X^*,mu^*) = 0).
- (Y^T abla_{XX}^2L(X^*,mu^*)Y>0 quad s.t. ;( abla_Xh(X))^TY = 0)
不等式约束条件
只包含一个不等式约束的优化问题
为了便于理解,我们设

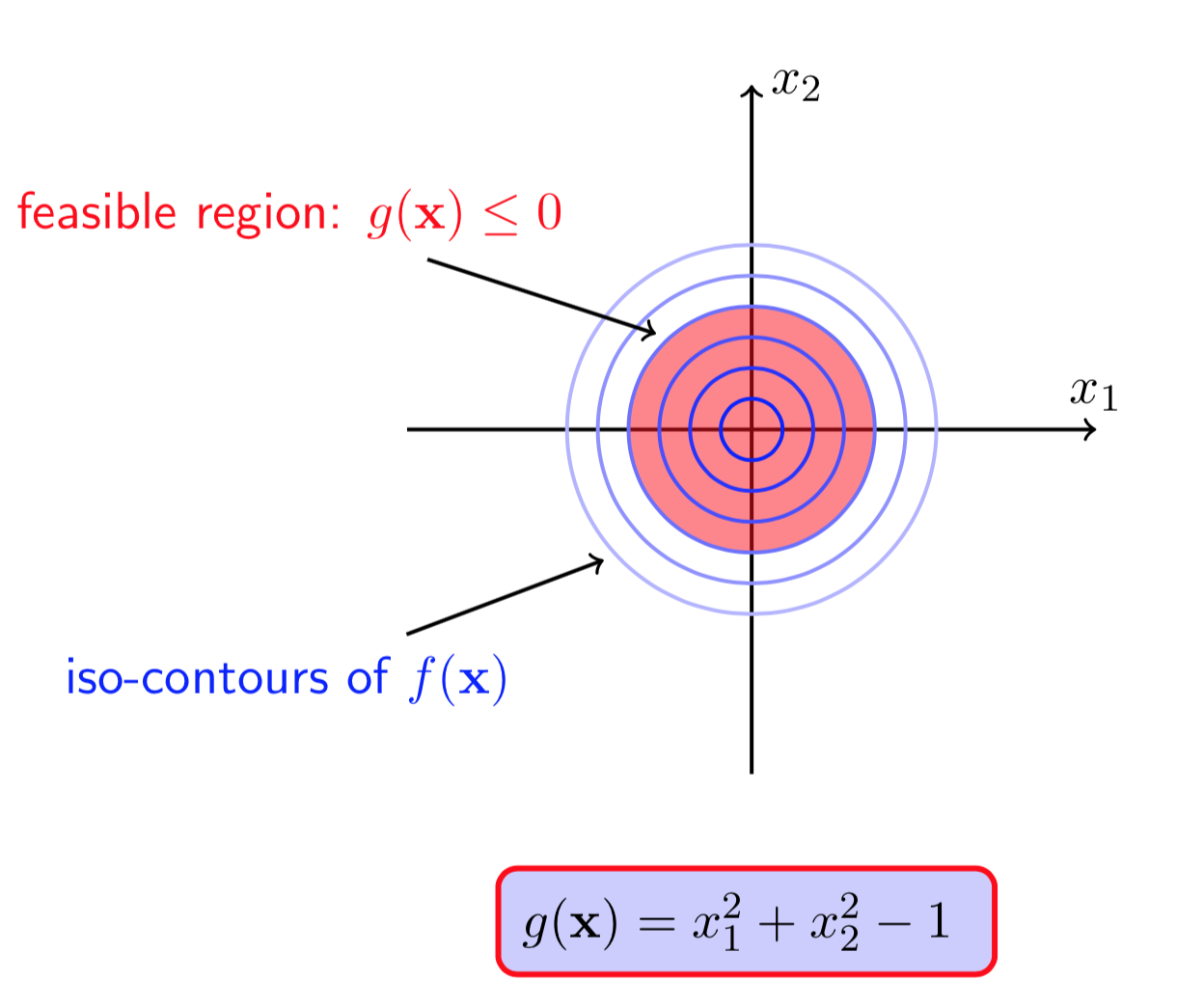
图(7 ) 图(8)
图(7)画出了(f(X))的等高线,并且点((0,0))是一个极小值点,图(8)的红色区域是在(g(X))约束条件下的可行域。从图中可以看出,无论是否有(g(X))的约束,函数(f(X))的极小值点都在((0,0))处,此时我们称该约束未被激活((g(X^*)<0)).现在,如果把目标函数修改成
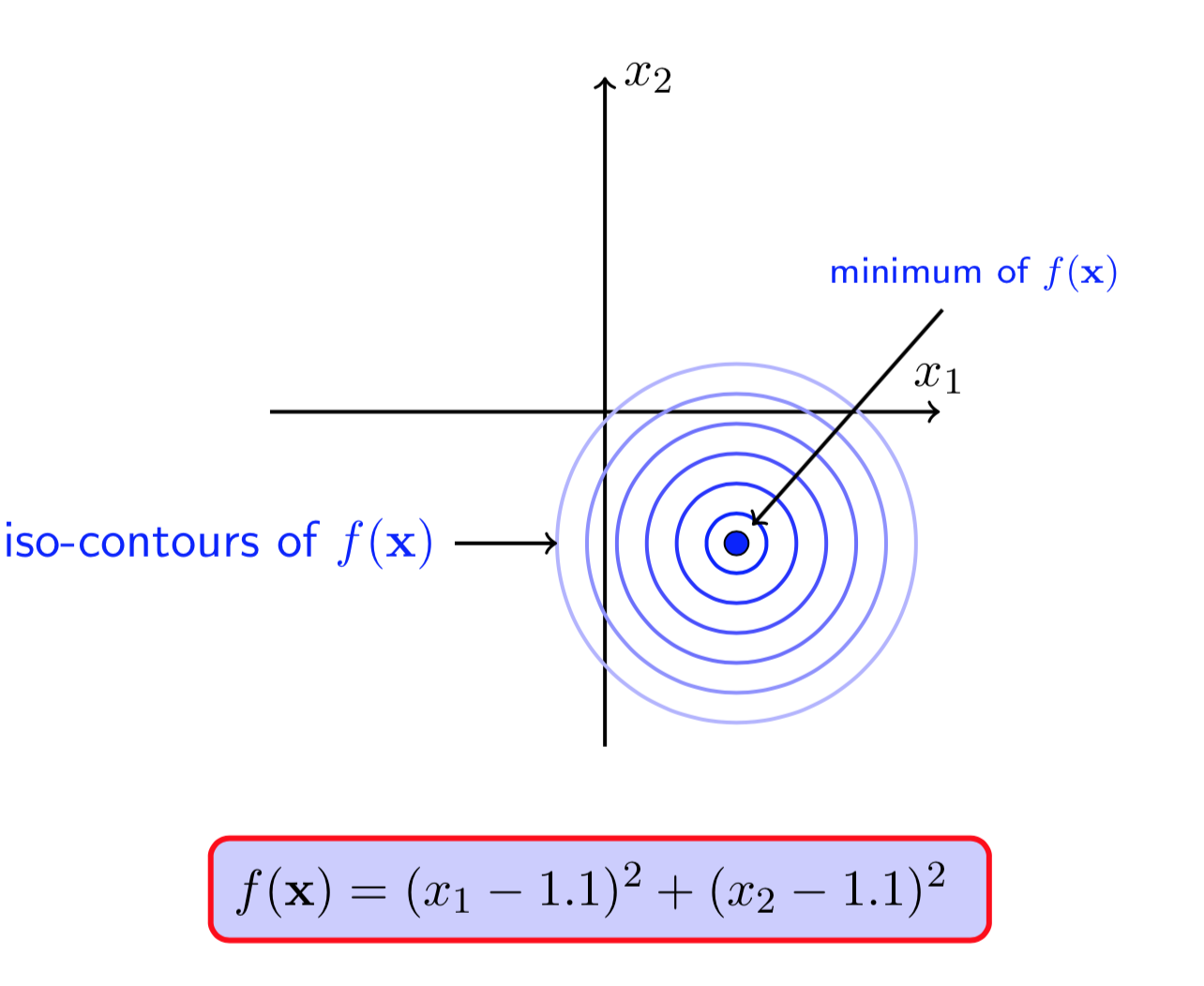
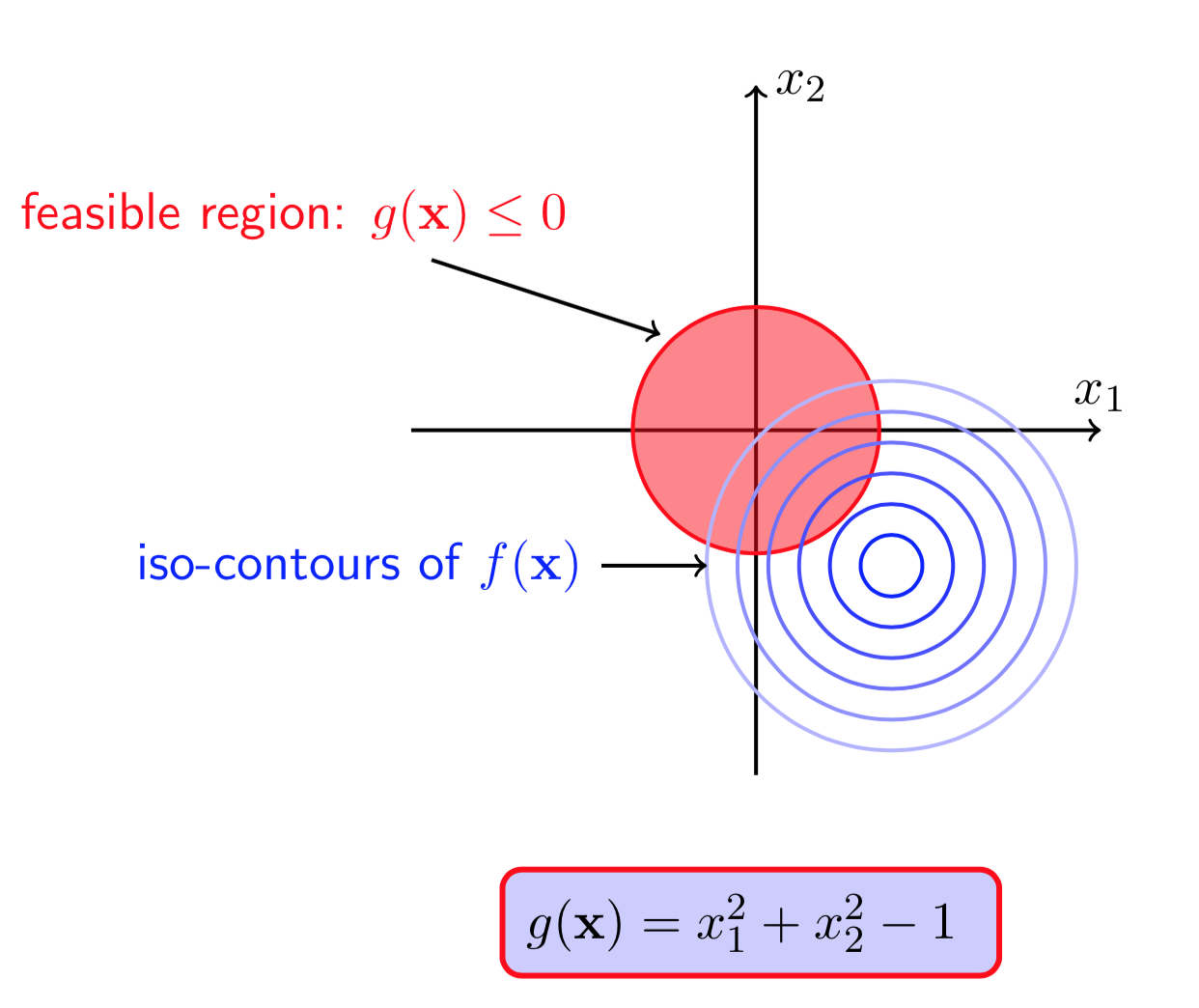
图(9 ) 图(10)
图(9)和(10)显示,(f(X))在无约束条件下的极值点是((1.1,1.1)),但是它并不在(g(X)leq0)的可行域中。这种情况下,若(X^*)是(f(X))满足约束条件的一个极小值点,那么一定有(g(X^*)=0),也即极小值点一定在约束的边界上取得。实际上,此处的不等式约束就变成了等式约束。
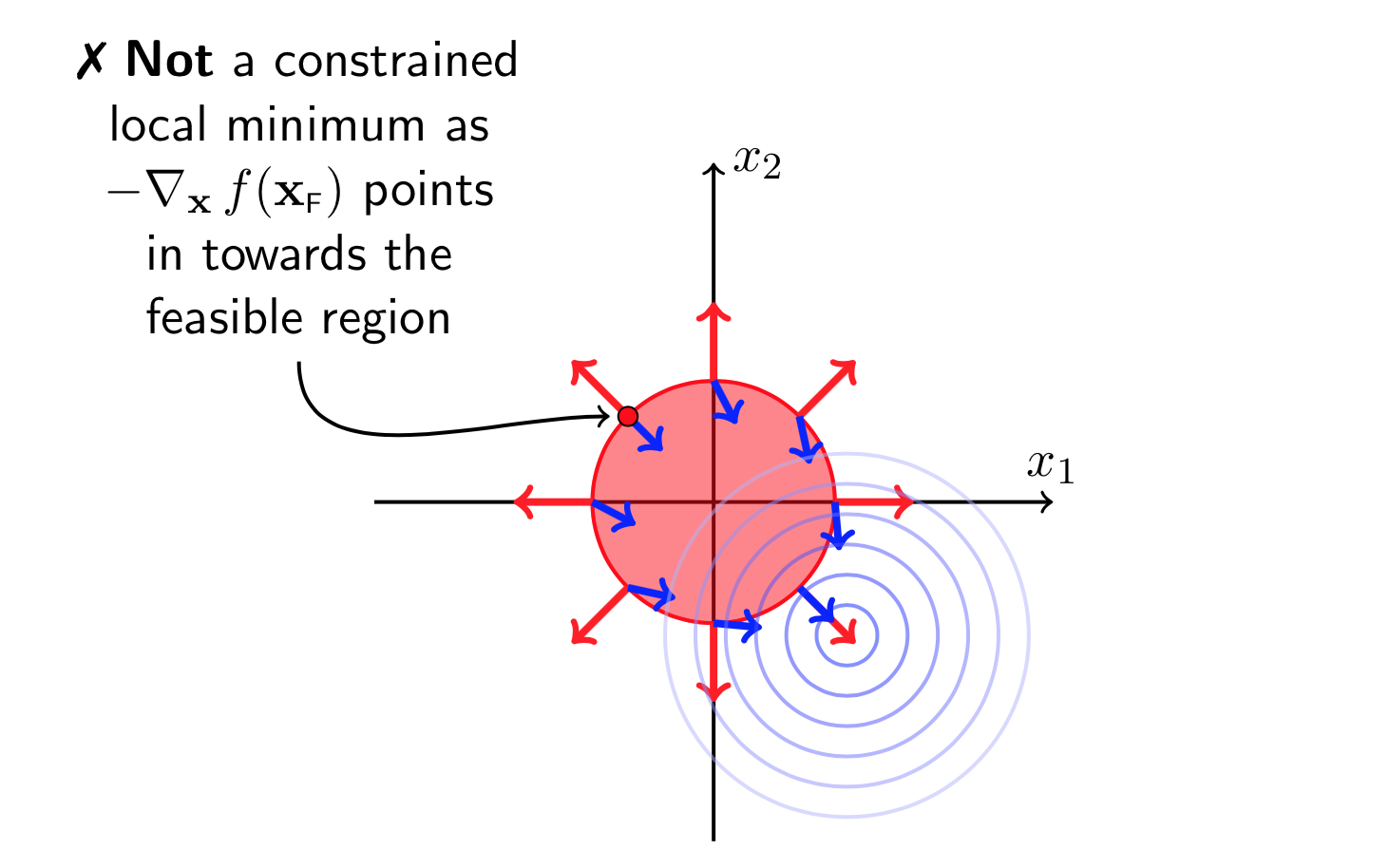
图(11)
从图(11)可以看出来,在极小值点处(- abla f(X))与( abla g(X))的方向是一致的
其实这也不难理解,如果说(X^*)是一个极小值点,上面分析知道(g(X)leq 0)被激活,所以(g(X^*)=0),如果设从点(X^*)出发下一步可行的方向为(Delta X),由于要满足(g(X^*+Delta X) leq 0),所以
所以下一步的所有可行方向需要满足上述不等式约束,因为(X^*)是一个极小值点,也就是说沿着满足上式(1)的(Delta X)的方向,都有$f(X^) leq f(X^+Delta X) $,也就是
并且我们知道(X^*)一定在(g(X)=0)上,通过上一节的等式约束的条件,应有
通过((1,2,3))式可知(mu leq 0),从而(lambda = -mu geq 0).
现在我们来总结一下上面讨论的结果,给出优化问题
如果(X^*)是一个极小值点,则可能有一下两种情况:
- Case 1: 无约束条件的极小值点出现在可行域内
- (g(X^*) < 0).
- ( abla _X f(X^*) = 0).
- ( abla^2 _{XX}f(X))是一个正定矩阵.
- Case 2: 无约束条件的极小值点出现在可行域外
- (g(X^*)=0).
- (- abla _Xf(X^*) = lambda abla g(X^*) quad where quad lambda > 0).
- (Y^T abla_{XX}^2L(X^*)Y geq 0 quad s.t. ;( abla_Xg(X^*))^TY = 0)
下面,直接引入(KKT)条件
定义拉格朗日函数
(X^*)是一个局部最小值等价于存在唯一的(lambda^*)满足
- KKT1 . ( abla _X L(X^*,lambda^*)=0).
- KKT2. (lambda ^* geq 0).
- KKT3. (lambda ^*g(X^*) = 0).
- KKT4. (g(X^*) leq 0).
- KKT5. 矩阵( abla _{XX}L(X^*,lambda ^*))正定.
上面就是(KKT)条件。这些条件其实可以分两种情况
- Case 1: 约束未激活
- 此时(lambda ^* = 0,L(X^*,lambda^*)=f(X^*)),
- KKT1 (Rightarrow abla _Xf(X^*)=0).
- KKT4 (Rightarrow X^*)是一个可行点
- Case 2: 约束被激活
- 此时(lambda ^* geq 0,L(X^*,lambda^*)=f(X^*)+lambda ^*g(X^*)),
- KKT1 (Rightarrow abla _Xf(X^*) =- lambda abla g(X^*)).
- KKT3 (Rightarrow g(X^*) = 0).并且(L(X^*,lambda^*)=f(X^*)).
将问题推广到多个不等式约束
定义拉格朗日函数
(X^*)是一个局部最小值等价于存在唯一的(lambda^*)满足
- KKT1 . ( abla _X L(X^*,lambda^*)=0).
- KKT2. (lambda _j^* geq 0quad j=1,2...,m).
- KKT3. (lambda_j^*g_j(X^*) = 0 quad j=1,2,...,m).
- KKT4. (g_j(X^*) leq 0 quad j=1,2,...,m).
- KKT5. 矩阵( abla _{XX}L(X^*,lambda ^*))正定.
同时存在等式和不等式约束
我们回到最开始的情况,同时存在多个等式约束和多个不等式约束
定义拉格朗日函数
(X^*)是一个局部最小值等价于存在唯一的(lambda^*)满足
- KKT1 . ( abla _X L(X^*,mu^*,lambda^*)=0).
- KKT2. (lambda _j^* geq 0quad j=1,2,...,m).
- KKT3. (lambda_j^*g_j(X^*) = 0 quad j=1,2,...,m).
- KKT4. (g_j(X^*) leq 0 quad j=1,2,...,m).
- KKT5. (h_i(X^*) = 0 quad i =1,2,...,l)
- KKT6. 矩阵( abla _{XX}L(X^*,lambda ^*))正定.
下面通过一个例子来加深理解,考虑问题
构造拉格朗日函数
KKT方程如下:
联立得
- 当(alpha ge 1/2)时,(lambda = 0 geq 2 -4 alpha),此时约束条件未被激活,原问题的最优解为((x_1,x_2)=(1/2,1/2)).
- 当(alpha < 1/2)时,(lambda = 2 - 4alpha > 0),从而(x_2-alpha = 0),即(x_2=alpha),此时约束条件被激活,愿问题最优解为((x_1,x_2)=(1-alpha,alpha)).