直线方程
只列出二维的情况,因为三维可以分解到二维来看。
斜率怎么算?写成 y = kx 的形式。
方向向量怎么算?斜率分子=y, 斜率分母=x。斜率就是 tan 夹角,对边比斜边,正好是方向向量的 step 。
法向量怎么算?法向量乘方向向量等于零(因为互相垂直)。
截距怎么算?令另一个轴坐标为零。
| 名称 | 形式 | 斜率 | 法向量 | 方向向量 | x 轴截距 | y 轴截距 |
|---|---|---|---|---|---|---|
| 一般式 | ax + by + c = 0 | -a / b | (a, b) | (b, -a) | -c / a | -c / b |
| 斜截式 | y = kx + b | k | (k, -1) | (1, k) | -b / k | b |
| 截距式 | x / a + y / b = 1 | -b / a | (1/a, 1/b) | (a, -b) | a | b |
| 点斜式 | y - y0 = k(x - x0) | k | (k, -1) | (1, k) | -y0/k + x0 | y0 - kx0 |
| 两点式 | (y - y0) / (y1 - y0) = (x - x0) / (x1 - x0) | (y1 - y0) / (x1 - x0) | (y1 - y0, x0-x1 ) | (x1-x0, y1 - y0) | ... | ... |
| 点向式 | (y - y0) / a = (x - x0) / b | ... | ... | ... | ... | ... |
| 点法式 | a(x - x0) + b(y - y0) = 0 | ... | ... | ... | ... | ... |
主要记住:
- 写成一般式过后,x 和 y 前面的系数就是法向量。
- 法向量与方向向量垂直。
平面方程
| 名称 | 形式 | 说明 |
|---|---|---|
| 一般式 | ax + by + cz + d = 0 | 法向量 (a, b, c) |
| 点法式 | a(x - x0) + b(y - y0) + c(z - z0) = 0 | 法向量 (a, b, c) |
| 截距式 | x/a + y/b + z/c = 1 | 截距 a, b, c |
对于一般式的平面方程要特别注意的情形有:
- 某些系数 = 0 : x 前系数为 0 说明平面垂直于 x 轴,x, y 前系数为 0 说明平面垂直于 xoy 平面。
- d = 0 :说明平面经过原点。
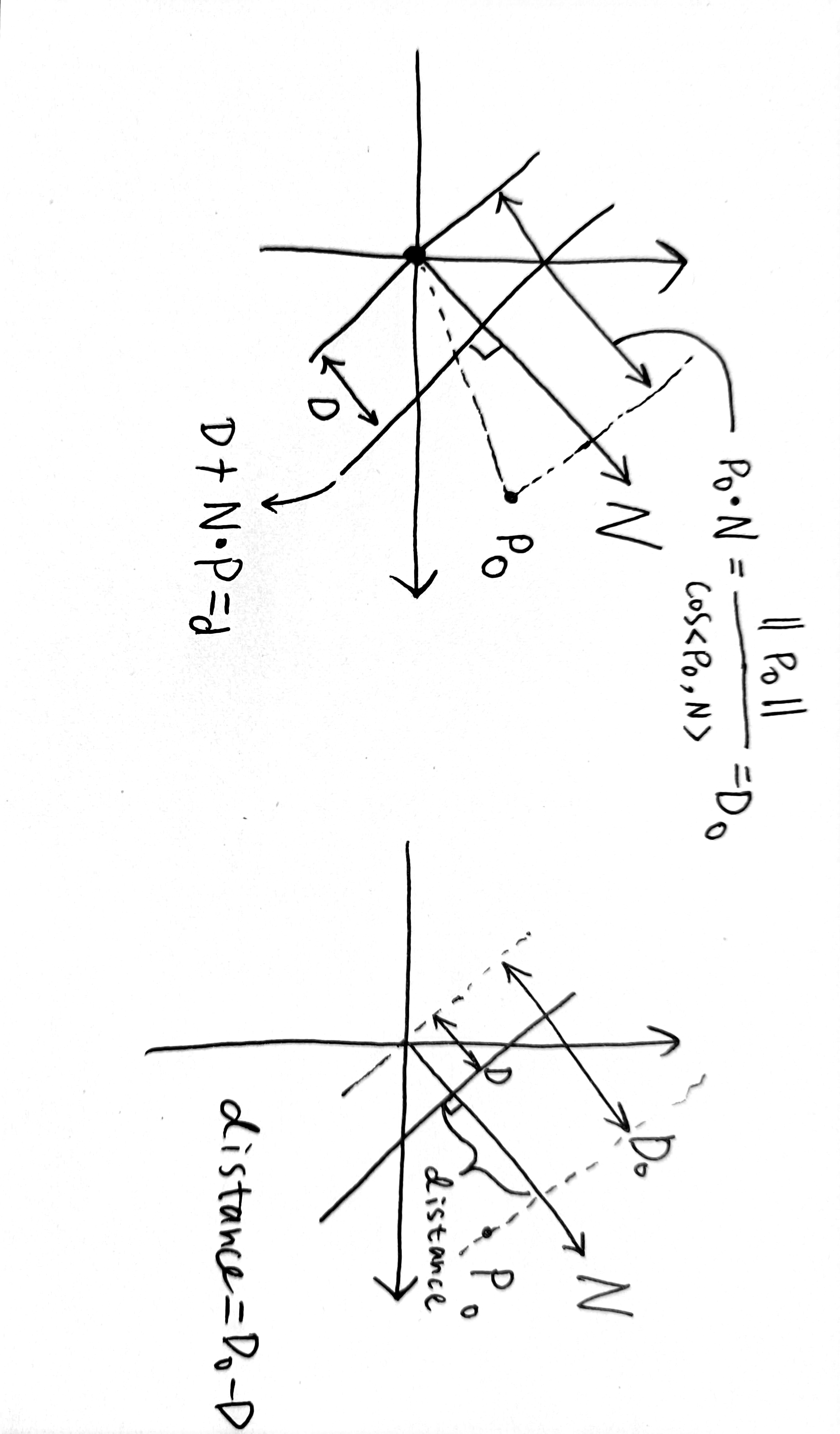
图形学里常用的形式是:N · P + D = d [1]。
N 代表法向量, P 代表平面上的一个已知点。这个式子可以从一般式推导出来:
ax + by + cz + d' = 0 可以写成 (a,b,c) · (x, y, z) + d' = 0 。令 (a,b,c) = N ,(x, y, z) = P ,d' = D - d 即可。
其中 D 是有几何意义的。考虑一般式中 d = 0 的情况。此时平面经过原点,且可以算出 :
| D | = | - N · P | = || N || || P || / cos<P, N>
那么 | D | / || N || = || P || / cos<P, N> 如下图所示。也就是说,当规定法向量为单位向量时,| D | 就是两个平面的距离。一个是给出的平面,一个是与给出平面平行且经过原点的平面。
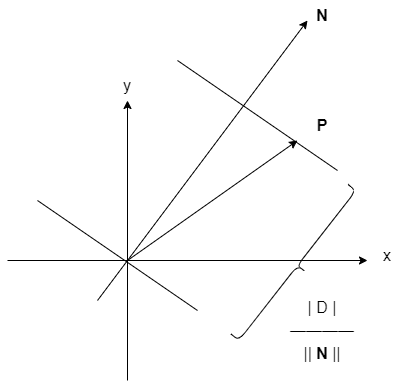
具体应用比如算平面外一点到平面的距离,设 Po 为平面外一点,那么 Po 到平面 N · P + D = d 的最短距离为 N · Po - D。
【DX 里我们 Vertex Shader 要输出的 SV_CullDistance,就是要算每个顶点到定义裁剪空间的平面的距离】
投影
Orthographic Projection
一个简单的正交投影:把点 (x, y, z) 投影到平面 z = 0 上变成 (x, y) 。特点:
- z 值不可还原。无论 z 是正是负都会变成 0 ,而且再也还原不回来。
- 类似于一个降低维度的操作。
正交投影更普遍的形式是把一个由 (l, r, t, b, n, f) 定义的 axis-aligned bounding box (AABB) 变成一个 中心在原点、轴对齐 的正方体[2]。
这个正方体叫做 canonical view volume (CVV),它里面点的坐标叫做 normalized device coordinates (NDC)。
DX 的 CVV 是 (-1,-1, 0) ~ (1, 1, 1) ,OpenGL 的 CVV 是 (-1, -1, -1) ~ (1, 1, 1) 。
e.g. 常见的俯视45度角就是 fixed 了一个 orthographic 的 camera。【拍自己脑阔:决定你 camera 看向哪里的是 lookat 的 y! 不是 up 的 y! 】
DX 有俩 Ortho 的 API :
XMMatrixOrthographic( float ViewWidth, float ViewHeight, float NearZ, float FarZ)
XMMatrixOrthographicOffCenter( float ViewLeft, float ViewRight, float ViewBottom, float ViewTop, float NearZ, float FarZ )
前者默认 AABB 的中心在原点,后者不在,所以要求给出 AABB 全部的六个参数。
// Initialize the view matrix
XMVECTOR Eye = XMVectorSet( -5.0f, 5.0f, -5.0f, 0.0f );
// 往45°那个方向,实际上是(1, -1, 1);如果纯 45° 应该是 (1/2, -sqrt(2)/2, 1/2)
XMVECTOR At = XMVectorSet( -4.0f, 4.0f, -4.0f, 0.0f );
XMVECTOR Up = XMVectorSet( 0.0f, 1.0f, 0.0f, 0.0f );
g_View = XMMatrixLookAtLH( Eye, At, Up );
// Initialize the orthographic projection matrix
g_Projection = XMMatrixOrthographicLH( 10, 10, 0.01f, 100.0f );
1 0 0 0
0 1 0 0
0 0 1 0 = T
-(l+r)/2 -(t+b)/2 -(n+f)/2 1
2/(r-l) 0 0 0
0 2/(t-b) 0 0
0 0 2/(f-n) 0 = S
0 0 0 1
首先做一个平移操作。拿 [l, r] 举例,让所有区间内的点都变成相对 (l+r)/2 的数,即 [l, r] 变成了 [l - (l+r)/2, r - (l+r)/2] = [(l-r)/2, (r-l)/2] = [-(r-l)/2, (r-l)/2]。接着是缩放操作,把 [-(r-l)/2, (r-l)/2] 除以 (r-l) 得到 [-1/2, 1/2] 然后乘2得到 [-1, 1] 。
应用上就是这样 v * M_ortho = v * T * S 。
Perspective Projection
// Initialize the view matrix
XMVECTOR Eye = XMVectorSet( -5.0f, 5.0f, -5.0f, 0.0f );
XMVECTOR At = XMVectorSet( -4.0f, 4.0f, -4.0f, 0.0f );
XMVECTOR Up = XMVectorSet( 0.0f, 1.0f, 0.0f, 0.0f );
g_View = XMMatrixLookAtLH( Eye, At, Up );
// Initialize the perspective projection matrix
g_Projection = XMMatrixPerspectiveFovLH( XM_PIDIV2, width / (FLOAT)height, 0.01f, 100.0f );