从二分问题到位向量

/*  
 * 文章脉络：
 *
 *     经典二分查找
 *         |
 *    -----------
 *    |         |
 * 整数溢出    拓展二分
 *    |         |
 *    |     ---------
 *    |     |       |
 *    |  整数二分  浮点数二分
 *    |     |       |
 *    ---------------
 *          |
 *       位向量理论
 */

1. 经典二分查找

Java 里的 bug 版二分查找代码[1]。出问题的代码是 (low + high)/2 ，这里会发生整数溢出。原因是
计算机是用位向量来代表连续数字的，而位向量的表示存在范围限制。这是要讨论的第一个问题： 位向量理论。

第二个要讨论的是二分查找问题的拓展。这里是一个二分查找算法，即在给定的有序数组中找出等于目标值的数的
下标。如果把查找中的“等于条件”拓展为某些其他性质，且此时的数组可以根据此性质二分，那么二分查找同样
适用。

    int binarySearch(int[] arr, int target){
        int low = 0;
        int high = arr.length - 1;

        // 三种分支情况
        while(low <= high){
            int middle = (low + high)/2;

            if(arr[middle] == target)
                return middle;

            if(arr[middle] > target)
                high = middle - 1;
            else
                low = middle + 1;
        }
        return -1;
    }

2. 拓展二分

2.1 整数二分 （下标是整数/离散情况）

给定一个有序数组和一种性质。这个数组里的元素，可以根据满不满足此性质，分成两个部分。这里有两种情况：

/*
 *     |-------- array --------|
 * (1) |--- unsat ---|-- sat --|
 * (2) |--- sat ---|-- unsat --|
 *
*/

（1） 分界处是，第一个，满足性质的元素；
（2） 分界处是，最后一个，满足性质的元素。

// 数组在上下文中

// 位置在 x 的元素满足性质吗？
bool sat(int x) { ... } 

// (1) [l, r] => [l, mid] [mid + 1, r]
int bsearch_1(int l, int r)
{
    // 两种分支情况
    while (l < r)
    {
        int mid = (l + r) / 2;

        if (sat(mid)) 
            r = mid;
        else 
            l = mid + 1;
    }
    return l;
}

// (2) [l, r] => [l, mid - 1] [mid, r]
int bsearch_2(int l, int r)
{
    while (l < r)
    {
        int mid = (l + r + 1) / 2;

        if (sat(mid)) 
            l = mid;
        else 
            r = mid - 1;
    }
    return l;
}

在第 2 种情况中，注意 (l + r + 1) 的处理。目的是防止死循环出现。举例，比如数组只有 2 个元素，那
么处理区间是 [0, 1]。求 mid 处不作 +1 处理的话，第一次 mid 为 0，倘若此处满足性质就会有
l = mid = 0，区间又变成了 [0, 1]，死循环。

2.2 浮点数二分 （下标是浮点数/连续情况）

// eps 表示精度，根据情况取值
const double eps = 1e-6;
double bsearch_3(double l, double r)
{
    while (r - l > eps)
    {
        double mid = (l + r) / 2;
        if (sat(mid)) r = mid;
        else l = mid;
    }
    return l;
}

浮点数的情况不会出现死循环 （为什么？）。由下述的位向量理论可知，浮点数的判等跟整数也不一样。

3. 位向量理论

计算机是离散的、是用一个个的位来表示数字。

3.1 整数

n bit 带符号整数 d 表示为：

d = [sign] d_n-2 * 2^(n-2) + ... + d1 * 2^1 + d0 * 2^0

sign = 0 表示正数，sign = 1 表示负数。

举例说明，最简单的情况，3个位的有符号整数，1个符号位，2个数值位。用补码表示：

二进制表示	十进制表示
0 1 1	3
0 1 0	2
0 0 1	1
0 0 0	0
1 0 0	-4
1 0 1	-3
1 1 0	-2
1 1 1	-1

用补码表示带符号整数要注意的地方：

1. 表示范围： n bit 的有符号整数能表示的范围是 [-2^(n-1), 2^(n-1)-1]。
   e.g. 3 bit 能表示 [-4, 3]。

2. 求补运算： 怎么求相反数的补码？从右到左找到第一个碰到的1，把它前面的所有位取反（包括符号位）。
   e.g. 2 的相反数 -2 的补码？2 = 010 => 110 = -2 。

3. 采用补码方案的原因？0不能有两种表示；计算机只会做加法，求补运算把减法变成了加法。

---

那什么情况下会溢出？

/*
1. 上溢

e.g. 2 + 2 = 5 > 3

  0 1 0
+ 0 1 0 
-0-1-0--
  1 0 0

100 = -4 != 5

2. 下溢

e.g. -3 - 2 = -5 < -4

  1 0 1
+ 1 1 0
-1-0-0--
  0 1 1

011 = 3 != -5
*/

直接给出结论：最高位（符号位）的进位与次高位的进位不一样，就溢出。即：

最高位进位 xor 次高位进位 == 1 就溢出

---

那么如何写对求两个有符号数的中位数呢？ 参考 Hacker's Delight book (section 2.5)：

t = (x & y) + ((x ^ y) >> 1)
t += ((t >> 31) & (x ^ y))

第一个是算数右移（补符号位），第二个是逻辑右移（补0）。

3.2 浮点数

编码的长度有限，所以进制表示法无法准确地表达有理数。小数的二进制表示只能表示那些能够被写成某个数乘上
2 的 n 次方的数，其他数只能被近似地表示。增加二进制的长度可以提高表示的精度。

3.2.1 IEEE 754 标准的 32 位浮点数

/*
      | sign | exponent | significand |
      | 31   | 30    23 | 22        0 |
 */

• 8 位阶码 （E）

  1. 阶码用移码表示 （e）

     移码是怎么来的？一个 8 位的有符号位向量，其表示范围为 [-127, 128]（零只取一个）。给它加上 127，
     表示范围就变成 [0, 255]。写成二进制就是 [0...0, 1...1]。这样就全变成正的了，不再需要符号位
     （但其表示的个数是不变的），计算方便许多。

  2. 全0 和 全1 的特殊阶码

     实际上用移码表示的阶码，全0 和 全 1 是用来表示特殊值的。尾数的意义会根据阶码的值有所不同。

• 23 位的尾数 （M）

  根据阶码的值，被编码的值可以被分成 4 种情况

  /* 
      | sign |   exponent    |      significand        |
      | s    | != 0 & != 255 |           f             |  规格化的    E = e - Biased, 0 <= f < 1, M = 1 + f
      | s    | 00000000      |           f             |  非规格化的  E = 1 - Biased, M = f
      | s    | 11111111      | 00000000000000000000000 |  无穷大
      | s    | 11111111      |          != 0           |  NaN
  */
  

  注意：非规格化数 M = f 的意思是，假设 f 是 2 位的，f = 0.11(B) = M = 0.75(O)。

  Biased （偏置值） = 2^(阶码位数 - 1) - 1

3.2.2 注意！注意！

3.2.2.1 非规格化数

• 非规格化数的用途？

1. 提供表示数值 0 的方法

使用规格化数， M >= 1 恒成立，无法表示 0 。其实， +0.0 的浮点表示法就是全0。其阶码为 0，意味着它
是一个非规格化数，所以 M = f = 0。而 -0.0 和 +0.0，在有些方面应该被认为不同，而其他方面相同。

2. 表示那些非常接近 0 的数

位向量的浮点表示法，可表示的数越靠近原点处分布得越密集。

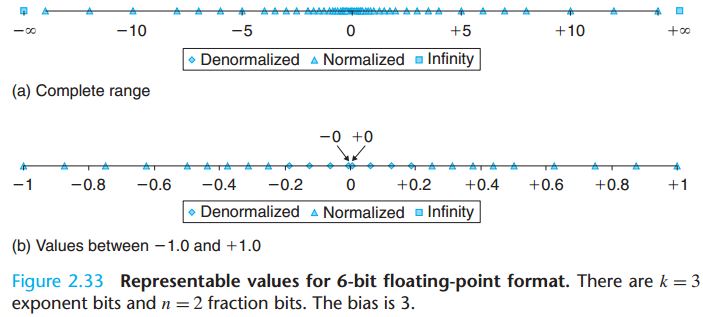
考虑这样一个简单的情况： 6 位浮点数！

/*
      | sign | exponent | significand | biased |
      | s    | xxx      | xx          | 3      |
 */

0 的两边浮点数分布一致，所以只考虑一边即可。不妨考虑正方向，符号位为 0 （正数）：

最大的非规格化数是多少？
0 000 11 = + (0.11B) × 2^(1-3) = + (3/4) × 2^(-2) = 3/16

最小的规格化数是多少？
0 001 00 = + (1.00B) × 2^(1-3) = + 1 × 2^(-2) = 1/4 = 4/16

可以观察到，最大的非规格化数 3/16 和最小的规格化数 4/16 之间的转变是平滑的，这是由非规格化数中，
E = 1 - Biased 这项规定来实现的。

如果 E = 0 - Biased 的话，最大的非规格化数就会是

(0.11B) × 2^(0-3) = (3/4) × 2^(-3) = 3/32

最小的规格化数是 3/16 = 8/32，他们之间的差距就比较大了。

3.2.2.2 舍入

因为表示方法限制了浮点数的范围和精度，所以浮点数只能近似表示实数运算。因此，对每一个值
x ，要找到最接近的浮点表示 x'。舍入（rouding）就是完成这项任务的方法。

IEEE 规定了四种舍入方法：向上舍入、向下舍入、向零舍入和向偶数舍入（默认方式）。

向偶数舍入(round-to-even) / 向最接近的值舍入(round-to-nearest)：

I 对不等于可能结果中间的值：舍入到最接近的那一端
II 对 等于可能结果中间的值：舍入到使得结果的最低有效数字是偶数

例 1 ：将小数舍入到最接近的正数（十进制表示）

1.40 => 1 (I)
1.60 => 2 (I)
1.50 => 2 (II)
2.50 => 2 (II)

例 2 ：舍入值到最近的四分之一（二进制表示）

10.00011 => 10.00 (I)
10.00110 => 10.01 (I)
10.11100 => 11.00 (II)
10.10100 => 11.10 (II)

为什么要用向偶数舍入？为了规避统计偏差。舍入一组值，总是把可表示值中间的数字向下/上舍
入，那舍入后的平均值就会比原来的略低/高。如果用向偶数舍入，它向上/向下舍
入的可能是 50% 。

3.2.2.3 运算

1 / (-0.0) = 负无穷
1 / (+0.0) = 正无穷

这里说明了浮点表示法中，+0 和 -0 此时不该被认为相同。

** 附注： IEEE 32 bit 浮点数的最值 **

FLOAT32_MAX = 0 11111110 11111111111111111111111
= + 2^(254-127) × (1 + (2^(-1) + ... + 2^(-23)))
= + 2^127 × (2 − 2^(-23))
≈ 3.4028235 × 10^38

INT32_MAX = 0 1111111111111111111111111111111
= + 2^31 − 1
= 2147483647
= 2.147483647 × 10^10

参考引用

[1] https://ai.googleblog.com/2006/06/extra-extra-read-all-about-it-nearly.html
[2] 二分查找的应用：两个有序数组的中位数 https://leetcode.com/problems/median-of-two-sorted-arrays
[3] 整数二分的应用：最长递增子序列 https://leetcode.com/problems/longest-increasing-subsequence/
[4] 浮点数二分的应用：sqrt(x) https://leetcode.com/problems/sqrtx/