
思路:
原来未排序的两数之和,解法用HashMap是较好的。
现在新加了一个排序过的特性,再联想起原来的两重for循环(顺序查找)
立马想到的是第二重查找时使用二分查找,这样时间复杂度变为nlogn,空间复杂度为O1
import java.util.Arrays; class Solution { public int[] twoSum(int[] numbers, int target) { for(int i=0;i<numbers.length;i++) { int j=Arrays.binarySearch(numbers,i+1,numbers.length,target-numbers[i]);//注意限定范围,否则可能会重复的出问题 if(j>0) { return new int[]{i+1,j+1}; } } return null; } }
这里因为二分法不是这里考察的重点,直接使用了自带的二分查找函数,另外这个数组部分查找原来是不知道的
然而一看答案有点傻眼,是哦,这里用双指针法可以用On的时间复杂度解决
直觉的想感觉可以理解,p1指头,p2指尾。比结果大则p2左移,比结果小则p1右移。
但是是不是这样老觉得还是会漏掉一些情况,这时我们可以用我们喜闻乐见的格子穷举
(缩减搜索空间)
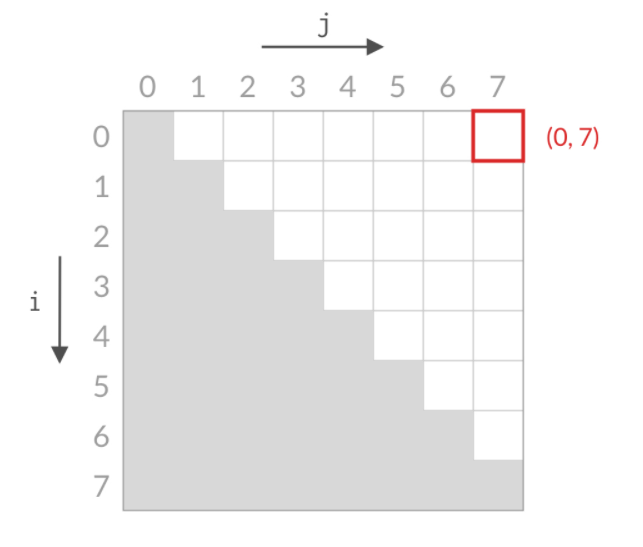
偏大则砍掉整一竖排(竖排大于等于顶点)
偏小则砍掉整一横排(横排小于等于顶点)

class Solution { public int[] twoSum(int[] numbers, int target) { int p1=0,p2=numbers.length-1; while(p1<p2) { if(numbers[p1]+numbers[p2]==target) {return new int[]{p1+1,p2+1};} else if(numbers[p1]+numbers[p2]>target) { p2--; } else if(numbers[p1]+numbers[p2]<target) { p1++; } } return null; } }