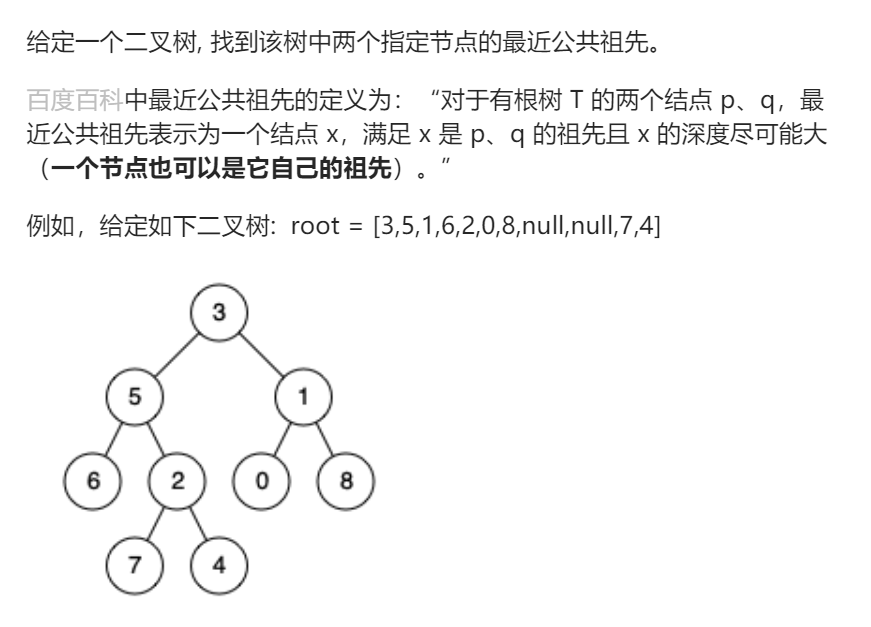

一看到这个题目,知道肯定是要搜索,而且至少从直觉上更接近深度优先搜索,因为明显更关注同一棵树,而不是同一层。
DFS实现的方式是递归,我们加上递归再来看看原来的DFS
void dfs(TreeNode root) { if (root == null) { return; }
root.val.sout();//打印出root的值 dfs(root.left); dfs(root.right); }
递归要从三个东西入手
- 递归函数要干什么
- 终止条件是什么
- 原函数的等价关系式
DFS的逻辑是这样:
- 函数的目标是打印出这棵树所有节点的值
- 终止条件是,这棵树为空(叶子节点再往下),直接return
- 打印出root树的所有节点==打印出root.val+打印出root左子树的所有节点+打印出root右子树所有节点
好,类比一下我们这道题:
- 函数的目标是找到这颗树中p和q的最近公共祖先
- 有一种终止条件容易想到:访问到叶子节点(且不为p/q)了,这意味着我们直觉上需要返回一个null,null意味着该树中没有p/q。另一种情况是访问到了p/q,怎么理解?有一种可能是p和q都在这棵以p为root的子树中,返回p很合理。还有一种情况是p这棵子树中没有q,返回p意味着这棵树中只有p,也很有信息。
- 现在到了等价关系。
- 如果左侧和右侧子树都返回null,意味着这棵树中完全不含p/q,返回null,很合理
- 左侧有p,右侧有q,恭喜,显然就是root本身。
- 如果左侧有p,右侧为null,意味着我们返回一个p(左侧树中有p,可能有p和q)。如果左侧有一个非p/q的值,说明已经找到了p和q的最近祖先了,直接返回。
说实话,这样虽然能解释的通,但是确实逻辑上不够完美。主要是这个递归函数的作用没有得到很好的解释。感觉有些牵强。。。
class Solution { public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) { if(root == null || root == p || root == q) return root; TreeNode left = lowestCommonAncestor(root.left, p, q); TreeNode right = lowestCommonAncestor(root.right, p, q); if(left == null) return right; if(right == null) return left; return root; } }