误差
误差( Error) :是模型的预测输出值与其真实值之间的差异。
训练( Training) : 通过已知的样本数据进行学习,从而得到模型的过程。
训练误差( Training Error) : 模型作用于训练集时的误差。
泛化( Generalize) :由具体的、个别的扩大为一般的,即从特殊到一般,称为泛化。对机器学习的模型来讲,泛化是指模型作用于新的样本数据(非训练集)。
泛化误差( Generalization Error) : 模型作用于新的样本数据时的误差。

欠拟合和过拟合
模型容量( Model Capacity) : 是指其拟合各种模型的能力。
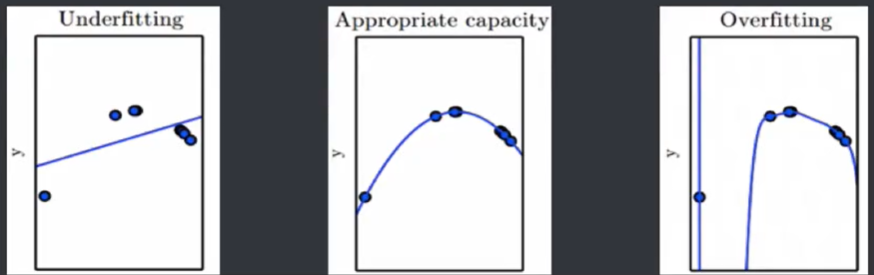
过拟合( Overfitting) : 是某个模型在训练集上表现很好,但是在新样本上表现差。模型将训练集的特征学习的太好,导致一些非普 遍规律被模型接纳和体现,从而在训练集上表现好,但是对于新样本表现差。反之则称为欠拟合( Underfitting) ,即模型对训练集的一般性质学习较差,模型作用于训练集时表现不好。
模型选择
模型选择( Model Selection) :针对某个具体的任务, 通常会有多种模型可供选择,对同一个模型也会有多组参数,可以通过分析、评估模型的泛化误差,选择泛化误差最小的模型。
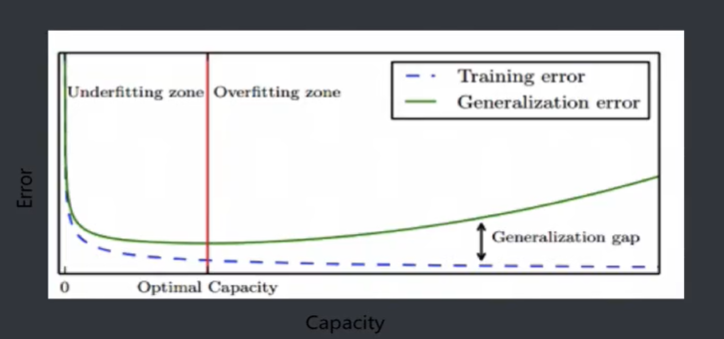
蓝色线越来越低接近于零,是训练误差越来越小,绿色的线是泛化误差,取红色的线,其二者都很小,这时的模型是可以的,过拟合的可能性会很小。
评估思路
通过实验测试,对模型的泛化误差进行评估,选出泛化误差最小的模型。待测数据集全集未知,使用测试集进行泛化测试,测试误差( Testing Error )即为泛化误差的近似。

留出法
留出法( Hold-out ) : 将已知数据集分成两个互斥的部分,其中一部分 用来训练模型,另一部分用来测试模型,评估其误差, 作为泛化误差的估计。
- 两个数据集的划分要尽可能保持数据分布一致性,避免因数据划分过程引入人为的偏差
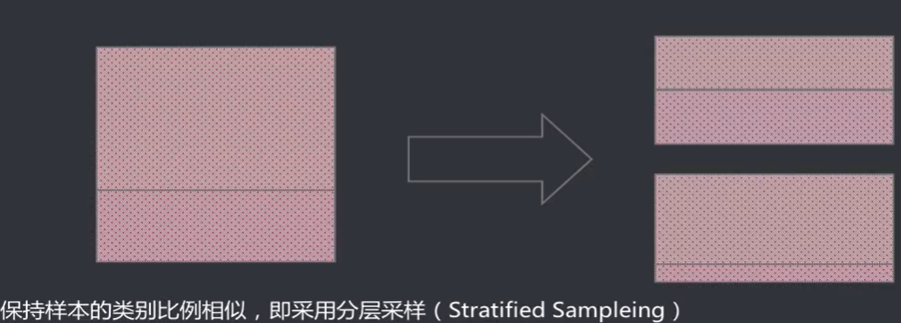
- 数据分割存在多种形式会导致不同的训练集、测试集划分,单次留出法结果往往存在偶然性,其稳定性较差,通常会进行若干次随机划分、重复实验评估取平均值作为评估结果
- 数据集拆分成两部分,每部分的规模设置会影响评估结果,测试、训练的比例通常为7:3、8:2等。大的比例去训练,小的去测试。
交叉验证法
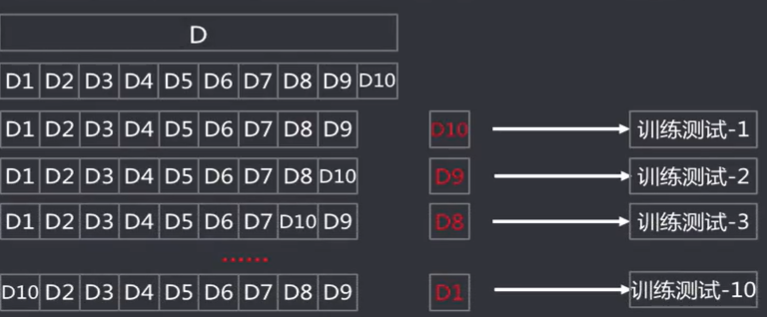
交叉验证法( Cross Validation) : 将数据集划分k个大小相似的互斥的数据子集,子集数据尽可能保证数据分布的一致性(分层采样) , 每次从中选取一个数据集作为测试集,其余用作训练集,可以进行k次训练和测试,得到评估均值。该验证方法也称作k折交叉验证( k-fold Cross Validation)。使用不同的划分,重复p次,称为p次k折交叉验证。
留一法
留一法( Leave-One-Out, LO0) :是k折交叉验证的特殊形式,将数据集分成两个,其中一个数据集记录条数为1 ,作为测试集使用,其余记录作为训练集训练模型。训练出的模型和使用全部数据集训练得到的模型接近,其评估结果比较准确。缺点是当数据集较大时,训练次数和计算规模较大。

一个为数据其他的都要训练,规模就比较大。
自助法
自助法( Bootstrapping) : 是一种产生样本的抽样方法,其实质是有放回的随机抽样。即从已知数据集中随机抽取一条记录,然后将该记录放入测试集同时放回原数据集,继续下一次抽样,直到测试集中的数据条数满足要求。

适用场景


性能度量
性能度量( Performance Measure) : 评价模型泛化能力的标准。对于不同的模型,有不同的评价标准,不同的评价标准将导致不同的评价结果。模型的好坏是相对的,取决于对于当前任务需求的完成情况。
回归模型的性能度量通常选用均方误差( Mean Squared Error )。


分类算法的性能度量

聚类算法的性能度量

模型比较
选择合适的评估方法和相应的性能度量,计算出性能度量后直接比较。
存在以下问题:

假设检验
统计假设检验( Hypothesis Test) : 事先对总体的参数或者分布做一个假设,然后基于已有的样本数据去判断这个假设是否合理。即样本和总体假设之间的不同是纯属机会变异(因为随机性误差导致的不同) , 还是两者确实不同。常用的假设检验方法有t-检验法、x2检验法(卡方检验)、F-检验法等。
