1. 前言
- 自然语言处理是关毅老师的研究生课程。
- 本博客仅对噪声信道模型、n元文法(N-gram语言模型)、维特比算法详细介绍。
- 其他的重点知识还包括概率上文无关文法(PCFG)、HMM形式化定义、词网格分词等等,比较简单,不做赘述。
2. 噪声信道模型
2.1 噪声信道模型原理
- 噪声信道模型的示意图如下所示:

- 该模型的目标是通过有噪声的输出信号试图恢复输入信号,依据贝叶斯公式,其计算公式如下所示:
[I = arg max _ { I } P ( I | O ) = arg max _ { I } frac { P ( O | I ) P ( I ) } { P ( O ) } = arg max _ { I } P ( O | I ) P ( I )
]
- (I)指输入信号,(O)指输出信号。
- 噪声模型的优点是具有普适性,通过修改噪声信道的定义,可以将很多常见的应用纳入到这一模型的框架之中,相关介绍见2.1。
2.2 噪声信道模型的应用
2.2.1 语音识别
- 语音识别的目的是通过声学信号,找到与其对应的置信度最大的语言文本。
- 计算公式与上文相同,此时的(I)为语言文本,(O)为声学信号。
- 代码实现过程中,有一个信息源以概率(P(I))生成语言文本,噪声信道以概率分布(P(O|I))将语言文本转换为声学信号。
- 模型通过贝叶斯公式对后验概率(P(I|O))进行计算。
2.2.2 其他应用
- 手写汉字识别
- 文本 -> 书写 -> 图像
- 文本校错
- 文本 -> 输入编辑 -> 带有错误的文本
- 音字转换
- 文本 -> 字音转换 -> 拼音编码
- 词性标注
- 词性标注序列 -> 词性词串替换 -> 词串
3. N-gram语言模型
3.1 N-gram语言模型原理
- N-gram语言模型基于马尔可夫假设,即下一个词的出现仅仅依赖于他前面的N个词,公式如下:
[P ( S ) = P left( w _ { 1 } w _ { 2 } dots w _ { n }
ight) = p left( w _ { 1 }
ight) p left( w _ { 2 } | w _ { 1 }
ight) p left( w _ { 3 } | w _ { 1 } w _ { 2 }
ight) ldots p left( w _ { n } | w _ { 1 } w _ { 2 } dots w _ { n - 1 }
ight)
]
- 实践中,往往采用最大似然估计的方式进行计算:
[P left( w _ { n } | w _ { 1 } w _ { 2 } dots w _ { n - 1 }
ight) = frac { C left( w _ { 1 } w _ { 2 } ldots w _ { n }
ight) } { C left( w _ { 1 } w _ { 2 } dots w _ { n - 1 }
ight) }
]
-
在训练语料库中统计获得字串的频度信息。
-
n越大: 对下一个词出现的约束性信息更多,更大的辨别力
-
n越小: 在训练语料库中出现的次数更多,更可靠的统计结果,更高的可靠性
3.2 平滑处理
- 如果不进行平滑处理,会面临数据稀疏的问题,这会使联合概率的其中一项值为0,从而导致句子的整体概率值为0。
3.2.1 加一平滑法(拉普拉斯定律)
- 公式如下:
[P _ { L a p } left( w _ { 1 } w _ { 2 } , ldots w _ { n }
ight) = frac { C left( w _ { 1 } w _ { 2 } dots w _ { n }
ight) + 1 } { N + B } , left( B = | V | ^ { n }
ight)
]
- 实际运算时,(N)为条件概率中先验字串的频度。
3.2.2 其他平滑方法
- Lidstone定律
- Good-Turing估计
- Back-off平滑
4. 维特比算法
4.1 维特比算法原理
- 维特比算法用于解决HMM三大问题中的解码问题,即给定一个输出字符序列和HMM模型参数,如何确定模型产生这一序列概率最大的状态序列。
[arg max _ { X } P ( X | O ) = arg max _ { X } frac { P ( X , O ) } { P ( O ) } = arg max _ { X } P ( X , O )
]
- (O)是输出字符序列,(X)是状态序列。
- 维特比算法迭代过程如下:
- 初始化
[egin{array} { l } { delta _ { 1 } ( i ) = pi _ { i } b _ { i } left( o _ { 1 }
ight) } \ { psi _ { 1 } ( i ) = 0 } end{array}
]
- 递归
[egin{array} { c } { delta _ { t + 1 } ( j ) = underset { 1 leq i leq N } max delta _ { t } ( i ) a _ { i j } b _ { j } left( o _ { t + 1 }
ight) } \ { psi _ { t + 1 } ( j ) = underset { 1 leq i leq N } { arg max } delta _ { t } ( i ) a _ { i j } b _ { j } left( o _ { t + 1 }
ight) } end{array}
]
- 结束
[egin{array} { c } { P ^ { * } = max _ { 1 leq i leq N } delta _ { T } ( i ) } \ { q _ { T } ^ { * } = underset { 1 leq i leq N } { arg max } delta _ { T } ( i ) } end{array}
]
- 最优路径(状态序列)
[q _ { t } ^ { * } = psi _ { t + 1 } left( q _ { t + 1 } ^ { * }
ight) , quad t = T - 1 , ldots , 1
]
- 上述迭代过程,(a)状态转移矩阵,(b)是状态-输出发射矩阵。
4.2 维特比算法例子
-
例子:
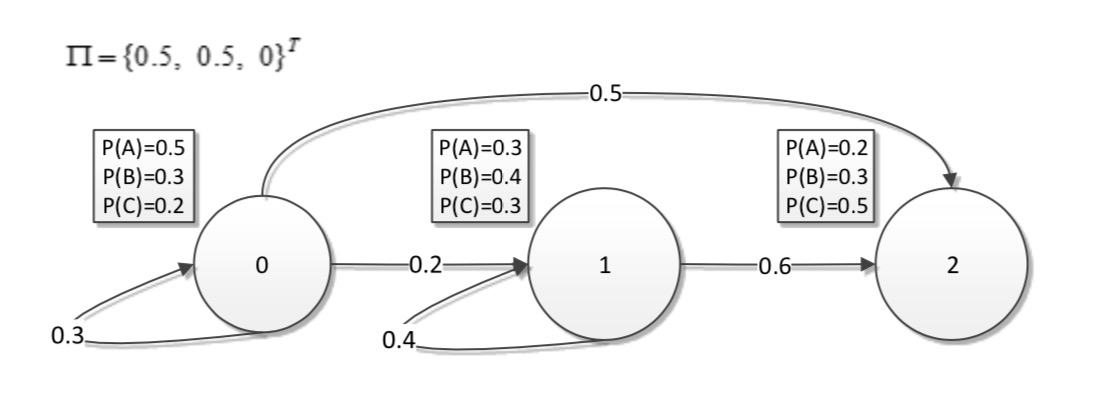
-
计算过程:
- 第一次迭代(此时的输出字符为A):
[delta _ { 1 } ( 0 ) = 0.5*0.5=0.25
]
[delta _ { 1 } ( 1 ) = 0.5*0.3=0.15
]
[delta _ { 1 } ( 2 ) = 0*0.2=0
]
- 第二次迭代(此时的输出字符为B):
[delta _ { 2 } ( 0 ) = max(0.25*0.3*0.3, 0, 0)=0.0225
]
[delta _ { 2 } ( 1 ) =max(0.25*0.2*0.4, 0.15*0.4*0.4, 0)=0.024
]
[delta _ { 2 } ( 2 ) = max(0.25*0.5*0.3, 0.15*0.6*0.3, 0)=0.0375
]
- 第三次迭代(此时的输出字符为C):
[delta _ { 3 } ( 0 ) = max(0.0225*0.3*0.2, 0, 0)=0.00135
]
[delta _ { 3 } ( 1 ) =max(0.0225*0.2*0.3, 0.024*0.4*0.3, 0)=0.00288
]
[delta _ { 3 } ( 2 ) =max(0.0225*0.5*0.5, 0.024*0.6*0.5, 0)=0.0072
]
-
最终答案:

- 选择最优路径的时候从后往前选,选择最后一列最大的概率值为最终结果。
- 即(0.0072))。
- 接着寻找上一步中生成该概率值((0.0072))的数作为前一步结果。
- 即(0.024),因为(0.024*0.6*0.5=0.0072)。
- 以此类推。
- 选择最优路径的时候从后往前选,选择最后一列最大的概率值为最终结果。
4.3 维特比算法应用
4.3.1 基于HMM的词性标注
- HMM的状态集合:词性标记集合
- (t_i)为为词性标记集合中的第(i)个词性标记。
- HMM的输出字符集合:词汇集合
- (pi _ { mathrm { i } }):词性标记(t_i)初始概率
- (a_{ij}):从词性标记(t_i)到(t_j)的状态转移概率
- (b_{jk}):词性标记(t_j)对应的词(w_k)的发射概率