一、A星寻路算法介绍
当你在制作一款游戏的时候是否想过让你的角色避开道路上的障碍物从而抵达终点呢?
如果有的话,那么这篇文章你要认真看下去,至少可以帮助你初步建立一个利用A星算法的思路实现它!
本篇文章将从算法最基本的思路讲起,让我们开始吧!
二、一张棋盘格

让我们来看这张图,你创造的主角小红,想要到达小黄所在的位置,这条线路我们应该怎么找。
显然图片中黑色的部分不像是小红能直接穿过的地方,我们需要绕一绕,也许你有很多条路可以走,但我现在告诉你,我们赶时间,我们需要找出最短的路!
如何解决这个问题呢,A星算法来了。
三、基本思路
我们将每个位置默认为一个正方格,他的目的是便于我们之后的计算
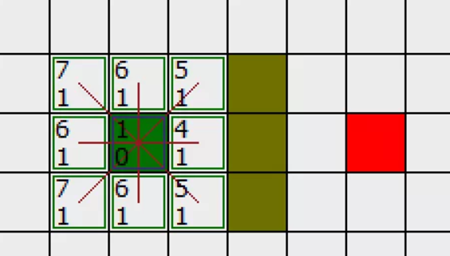
不要质疑为什么你的主角变了颜色,这并不影响我们的讲解。
我们创造了一个简单的搜索区域,八个方向,并且我们用小本本记下了两个列表:open列表(记录下所有被考虑来寻找最短路径的方块) 和 close列表(记录下不会再被考虑的方块)
首先我们将起点添加入close列表中(我们将起点设为“A”,深绿色方框),再将A附近所有可行方块添加入open列表中(绿色描边方框)
路径增量
我们给每一个方块一个G+H和值
G为从起点A到当前点的移动量(代表本文中的方块数量),所以从A开始到相邻点的G值为1,这个值会随着角色的移动(或者说距离开始点)越来越远而增大。
H为从当前所在点到终点(我们将它设为B!)的移动估算量,这个常被成为探视,因为我们不确定它的移动量的准确数值,所以这个H仅仅只是一个估算值。
(值得一提的是,这个H的估算值我们有多种办法算取,你可以使用“曼哈顿距离算法”,或是欧拉公式等,它只是计算出点B剩下的水平垂直方块的数量,忽略掉中途的任何障碍物)
在A星算法中移动量这个值是由你来决定的,你可以仅仅允许主角进行上下左右四个方向的移动,或者你可以将移动量针对地形调整到大一点。
四、算法原理
既然你已经知道G和F,我们来认识一下这个算法最核心的值——F值,它有一个公式:F=G+H,它的意义是方块的移动总代价(或称为和值)
在算法中,角色将重复下列几个步骤来寻找最短路径:
1,将方块添加到open列表中,且该方块拥有最小的F和值,我们暂且将它称为S。
2、将其从open列表中移除,然后添加入close列表中。
3、对于S相邻的每一个方块,都有:
若该方块在close列表中,我们不管它。
若改方块不在open列表中,计算它的F和值并将其添加入open列表中。
若该方块已经在open列表中,当我们沿着当前路径到达它时,计算它的F和值是否更小,如果是,前进并更新它的和值和它的前继。
为了帮助你理解它的原理,我们来举个例子吧:
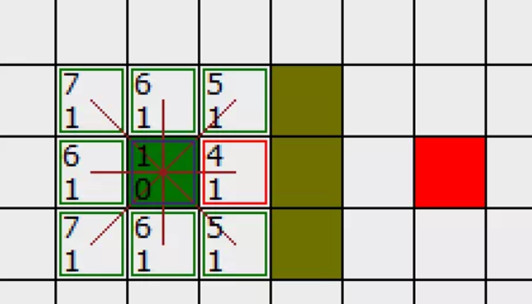
在接下来的每一步中,绿色方框代表我们可以选择的方块,而已选择的方块我们会用红色边框将它点亮。
第一步,我们要确定起点附近的每一个方块,计算他们的F值并将其添加入open列表中,在图片中,方框左下方的数字代表G值,为了确保你学会了怎么使用“截取距离算法(忽略障碍物由A到B的位移量)”H值,我们不打算将其标入方框中,最终,将G与你计算出的H值相加便得到左上角的F和值。
第二步,选择其中F值最小的方块并将其添加入close列表中,再次检索它相邻的可行方块,我们发现有两个一模一样的方块可选,而根据刚才讲到的第三条定理,我们发现上下两个方块都已经在open列表中,且我们通过计算发现,第一步时它的G值为1,但当我们经由当前已在的“4,1”方格在到达那里时,它的G值将变为2(因为我们绕了一下,所以移动了两步),显然2比1大,因此从“4,1”再走到“5,1”并不是最优路径,我相信你是一个有远见的人,所以你会从第一步就选择“5,1”方块。
第三步、当你选择走最优路径时,你会发现一个问题,“5,1”方块有两个,也就是说有两条一模一样的路可以走,但真的是这样吗,我们保留这个疑问,随便选择一个,比如我选择走上边的“5,1”方块。
再次检索周围方块,并忽略掉障碍物。我们得到如下图的信息。
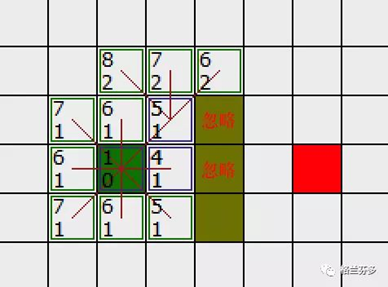
我们发现有好几个F值都为6的,没关系,我们都考虑上并计算他附近的F值,在这里我们也顺便将刚才未选择的下方“5,1”方块周围的F值计算一下
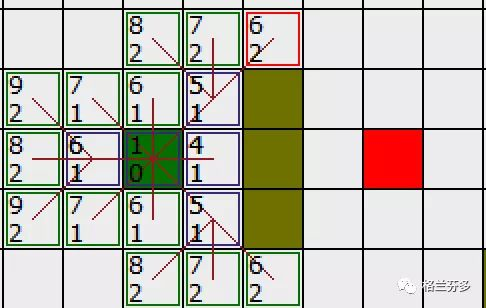
可以看到其实左边的方块其实是不用考虑的,我们人眼一看就知道接着刚才的路继续寻找就好了,但是程序并不知道,他只会老老实实运行你给他规定的步骤,这算是必踩的坑。
但是有一种比较简便的方法是,规定一直沿着最近被添加入open列表的方块。
好了现在你已经训练有素了,经过几次重复你得到了下图这样的路径
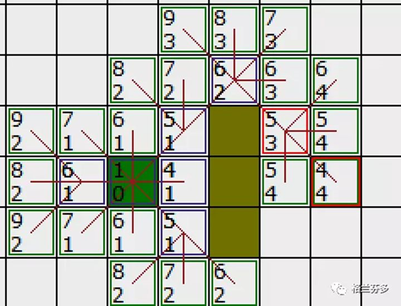
你成功到达了终点,他已经在open列表中了,当你迈出最后一步时,程序会将它从open中移除并添加入close列表中。
最后,算法,算法需要做的是就是沿着路径返回并计算出最优路径。
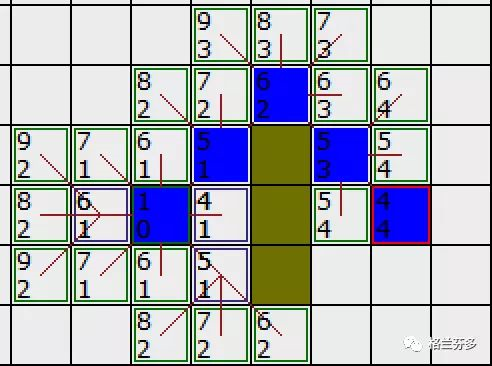
让我们将最终路径用蓝色方框强调出来。
代码部分
<!DOCTYPE html>
<html>
<head>
<meta charset="UTF-8">
<title></title>
<style type="text/css">
#ul1{
margin: 30px auto;
border: 1px solid black;
border-bottom: none;
border-right:none ;
padding: 0;
height: auto;
overflow: hidden;
}
#ul1 li{
list-style: none;
border: 1px solid black;
border-top:none ;
border-left:none ;
float: left;
}
#ul1 li.style1{
background-color: red;
}
#ul1 li.style2{
background-color: black;
}
#ul1 li.style3{
background-color: orange;
}
#btn{
position: absolute;
left: 50%;
margin-left: -50px;
}
#btn:hover{
background-color: #E21918;
color: white;
border-radius: 4px;
}
</style>
</head>
<body>
<ul id="ul1">
</ul>
<input id="btn" type="button" value="开始寻路"/>
<script type="text/javascript">
var oUl = document.getElementById("ul1");
var aLi = document.getElementsByTagName("li");
var beginLi = document.getElementsByClassName("style1");
var endLi = document.getElementsByClassName("style3");
var oBtn = document.getElementById("btn")
//算法实现
/**
* open队列: 收集可能会需要走的路线 要走的路线放在open队列中
* close队列: 排除掉不能走的路线 不走的路线放在close队列中
*
*/
//可能要走的路线
var openArr = []
//已经关闭的路线
var closeArr = []
var map = [
0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,
0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,
0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,
0,0,0,0,0,0,0,0,2,0,0,0,0,0,0,0,0,0,0,0,
0,0,0,0,0,0,0,0,2,0,0,0,0,0,0,0,0,0,0,0,
0,0,0,0,0,0,0,0,2,0,0,0,0,0,0,0,0,0,0,0,
0,0,0,0,0,0,0,0,2,2,2,2,0,0,0,0,3,0,0,0,
0,0,0,0,0,0,0,0,0,0,0,2,0,0,0,0,0,0,0,0,
0,0,0,0,0,0,0,0,1,0,0,2,0,0,0,0,0,0,0,0,
0,0,0,0,0,0,0,0,0,0,0,2,0,0,0,0,0,0,0,0,
0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,
0,0,0,0,0,0,0,0,0,2,0,0,0,0,0,0,0,0,0,0,
2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,
0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,
0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,
0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,
0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,
0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,
0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,
0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0
]
//最终线路数组
var resultParent = [];
init();
//初始化函数
function init(){
createMap()
//点击按钮的时候 需要去收集可能走的路线
oBtn.onclick = function(){
openFn();
}
}
//创建地图
function createMap(){
var liSize = 20;
for(var i=0;i<map.length;i++){
var oLi = document.createElement("li");
oLi.style.width = liSize +"px";
oLi.style.height = liSize + "px";
oUl.appendChild(oLi);
if(map[i]==1){
oLi.className = "style1";
//当元素刚开始创建的时候,open队列中的元素只有 起始节点 也就是说将红色点都放到open队列中 并且 刚开始的时候 起始点只有一个
openArr.push(oLi);
}else if(map[i]==2){
//当元素刚刚开始创建的时候 close队列中的元素 就是 值为2的元素 也就是说 把黑色的点都放到close队列中 这些作为障碍物 是不会走的
oLi.className = "style2";
closeArr.push(oLi);
}else if(map[i]==3){
oLi.className = "style3"
}
}
//ul的宽带等于 ul的左边 1 + 20个节点的宽带 20*(liSize+1) 其中 liSize+1 是因为 节点有1个像素的右边框
oUl.style.width = 20*(liSize+1)+1+"px"
}
//估价函数
function fn(nowLi){
return g(nowLi)+h(nowLi)
}
//初始点到当前节点的实际代价
function g(nowLi){
//勾股定理
var a = nowLi.offsetLeft-beginLi[0].offsetLeft;
var b = nowLi.offsetTop - beginLi[0].offsetTop;
return Math.sqrt(a*a+b*b)
}
//当前节点到目标点的实际代价
function h(nowLi){
//勾股定理
var a = nowLi.offsetLeft-endLi[0].offsetLeft;
var b = nowLi.offsetTop - endLi[0].offsetTop;
return Math.sqrt(a*a+b*b)
}
/**
* 实现的功能: 1 把open队列中的元素移到close队列中,表示起始节点已经走过了,那么接下来应该走哪一步呢?
* 2 把起始位置周围的 8 个点都找出来 并且 计算出 估价函数值最低的那个元素 那么这个元素就是接下来要走的这步
* 3 接下来走的这步确定了 那么就又该把这个位置的点移动到 close队列中,然后继续找周围的点 并且进行估价 以此类推
*/
function openFn(){
//nodeLi 表示 当前open队列中的元素 也就是说 先去除第一个起始节点
//shift 方法的作用: 把数组中的第一个元素删除,并且返回这个被删除的元素
var nodeLi = openArr.shift();
//如果nodeLi 和 endLi 一样了 那么证明已经走到目标点了 ,这个时候需要停止调用
if(nodeLi == endLi[0]){
showPath();
return;
}
//把open队列中删除的元素 添加到 close队列中
closeFn(nodeLi)
//接下来 需要找到 nodeLi 周围的节点
findLi(nodeLi);
//经过上面的步骤 已经能够找到相邻的元素了 接下来需要对这些元素的估值进行排序
openArr.sort(function(li1,li2){
return li1.num - li2.num
})
//进行递归操作 找下一步需要走的节点 在这个过程中,也需要执行相同的步骤 那就是查找相邻的节点 但是查找出来的结果可能和上一次的重复,也就是说上一次动作已经把这个元素添加到open队列中了
//那么就没有必要再进行push操作了 所以还需要在过滤函数中加一段代码
openFn();
}
function closeFn(nodeLi){
//open队列中删除的元素 被 push到close队列中
closeArr.push(nodeLi);
}
/**
* 封装函数查找某个节点周围的节点
*/
function findLi(nodeLi){
//创建一个结果数组 把查找到的结果放到这个数组中
var result = [];
//循环所有的li节点 进行查找
for(var i=0;i<aLi.length;i++){
//如果经过过滤 返回的是true 表示 这个节点不是障碍物 那么需要添加到result结果数组中
if(filter(aLi[i])){
result.push(aLi[i]);
}
}
//接下来需要在没有障碍物的结果中去找 和 当前节点相邻的节点
//判断条件是 他们的横纵坐标的差值需要小于 等于 网格大小
for(var i=0;i<result.length;i++){
if(Math.abs(nodeLi.offsetLeft - result[i].offsetLeft)<=21 && Math.abs(nodeLi.offsetTop - result[i].offsetTop)<=20+1 ){
//这里的result[i]就是当前目标点相邻的节点 把这些节点传入到估价函数就能得到他们的估值,并且要把这些估值挂载到他们自身的一个自定义属性上
result[i].num = fn(result[i]);
//nodeLi 是当前的位置 result[i] 是当前位置相邻的点 下一次要走的位置就在这几个点中,所以给result[i]定义一个parent属性
//来存上一次的路径 ,最终把这些路径联系起来就是完整的路径
result[i].parent = nodeLi;
openArr.push(result[i]);
}
}
}
/**
* 封装函数 实现过滤功能
* 这个函数的功能就是 接收到一个li 判断是否是障碍物 如果是 就返回false 如果不是就返回true
*/
function filter(nodeLi){
//循环close队列中的所有元素 与传过来的节点进行比对 如果比对成功 返回false
for(var i=0;i<closeArr.length;i++){
if(nodeLi == closeArr[i]){
return false;
}
}
for(var i=0;i<openArr.length;i++){
if(nodeLi == openArr[i]){
return false;
}
}
//如果循环完都没有匹配上 那么证明当前传过来的 li节点 并不是障碍物
return true;
}
/**
* 打印出所走过的路径
*/
function showPath(){
//closeArr中最后一个 就是 找到目标点的前一个位置 因为走过的位置都会被存放在closeArr中
var lastLi = closeArr.pop();
var iNow = 0;
//调用findParent函数 来找上一个节点
findParent(lastLi)
var timer = setInterval(function(){
resultParent[iNow].style.background = "red";
iNow++;
if(iNow == resultParent.length){
clearInterval(timer);
}
},500)
}
/**
* 定义一个函数来找到上一次走过的节点
*/
function findParent(li){
resultParent.unshift(li);
if(li.parent == beginLi[0]){
return;
}
findParent(li.parent);
}
</script>
</body>
</html>
(我们在该代码中使用的是勾股定理来计算,实际上与街区算法原理)
这便是所有代码部分了,其中都包含有对每部分的注释讲解,读者可自行阅读理解。
运行结果
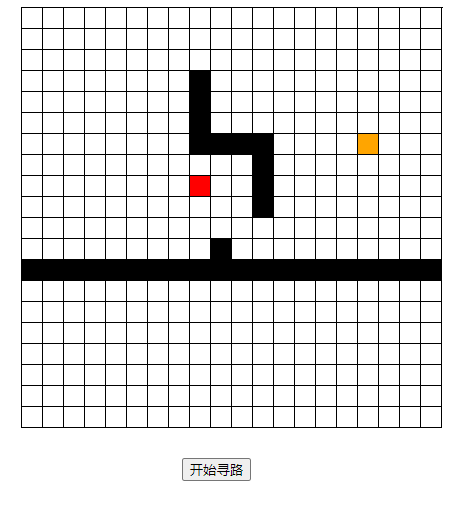
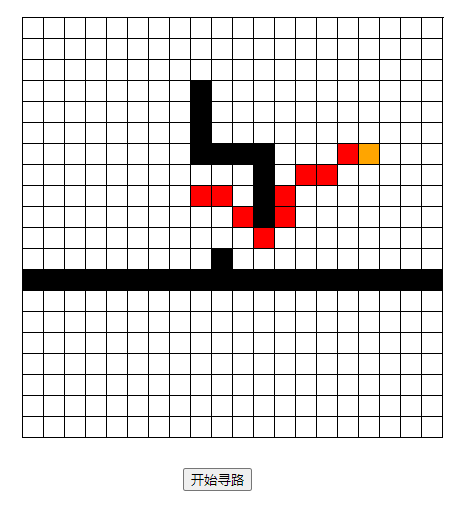
我在这里插入一个比较优秀的A星算法演示链接,方便各位理解算法思路。
http://qiao.github.io/PathFinding.js/visual/
成品展示链接
链接:https://pan.baidu.com/s/1Y4OaovodEtBeXUCRdOKDIg
提取码:dt68
小组成员:杨豪杰 刘益 谢君 杨千禧