题目描述
有 n 个同学(编号为 1 到 n )正在玩一个信息传递的游戏。在游戏里每人都有一个固定的信息传递对象,其中,编号为 i 的同学的信息传递对象是编号为 Ti 的同学。
游戏开始时,每人都只知道自己的生日。之后每一轮中,所有人会同时将自己当前所知的生日信息告诉各自的信息传递对象(注意:可能有人可以从若干人那里获取信息, 但是每人只会把信息告诉一个人,即自己的信息传递对象)。当有人从别人口中得知自 己的生日时,游戏结束。请问该游戏一共可以进行几轮?
输入输出格式
输入格式:
共2行。
第1行包含1个正整数 n ,表示 n 个人。
第2行包含 n 个用空格隔开的正整数 T1,T2,⋯⋯,Tn ,其中第i个整数Ti表示编号为i的同学的信息传递对象是编号为Ti的同学,Ti≤n 且Ti≠i 。
输出格式:
1个整数,表示游戏一共可以进行多少轮。
输入输出样例
说明
样例1解释
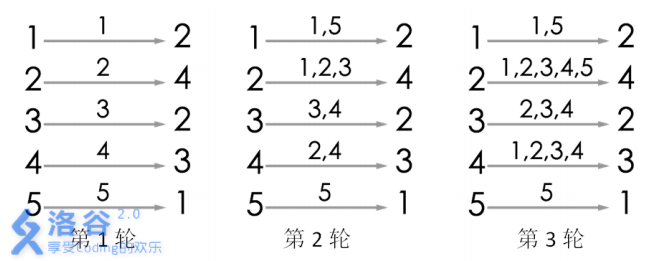
游戏的流程如图所示。当进行完第3轮游戏后, 4号玩家会听到 2 号玩家告诉他自己的生日,所以答案为 3。当然,第 3 轮游戏后,2号玩家、 3 号玩家都能从自己的消息来源得知自己的生日,同样符合游戏结束的条件。
对于 30%的数据, n ≤ 200;
对于 60%的数据, n ≤ 2500;
对于 100%的数据, n ≤ 200000。
解析:
这道题很明显的搜索+剪枝,当然也可以用并查集去求最小环,本人是用的搜索+剪枝。
每个节点搜索一次,这里运用到的剪枝技巧是搜索过的节点记录一下,不再搜索,在下面的代码中,vis[i]表示在本轮搜索中搜索过i号节点,no[i]表示之前的搜索过程中已经搜索过i号节点,如果已经搜索过i号节点的话,那么它拓展出来的环也肯定已经搜索过了,所以说当然就不必再搜一次了,更不会访问到vis[i],所以vis数组也不用清空,虽然是搜索算法,可是每个节点最多只搜索过一次,所以这个程序依旧是线性的,已经到达了理论下界(读取数据也需要线性的复杂度);下边上代码:

1 #include<iostream> 2 #include<cstdio> 3 #include<cstring> 4 using namespace std; 5 int n,a[200001],dist[200001],minn=21374404; 6 bool vis[200001],no[200001]; 7 int read() 8 { 9 int f=1,x=0; 10 char s=getchar(); 11 while(s<'0'||s>'9'){if(s=='-')f=-1;s=getchar();} 12 while(s>='0'&&s<='9'){x=x*10+s-'0';s=getchar();} 13 return x*f; 14 } 15 void dfs(int now,int d) 16 { 17 if(no[now])return; 18 if(vis[now]) 19 { 20 minn=min(minn,d-dist[now]); 21 return; 22 } 23 vis[now]=1; 24 dist[now]=d; 25 dfs(a[now],d+1); 26 no[now]=1; 27 } 28 int main() 29 { 30 n=read(); 31 for(int i=1;i<=n;i++) 32 { 33 a[i]=read(); 34 } 35 for(int i=1;i<=n;i++) 36 { 37 dfs(i,0); 38 } 39 cout<<minn; 40 return 0; 41 }
