题目描述
小明和小红在玩欧几里得游戏。他们从两个自然数开始,第一个玩家小明,从两个数的较大数中减去较小数的尽可能大的正整数倍,只要差为非负即可。然后,第二个玩家小红,对得到的两个数进行同样的操作,然后又是小明。就这样轮流进行游戏,直至某个玩家将较大数减去较小数的某个倍数之后差为0为止,此时游戏结束,该玩家就是胜利者。
输入
输入包含多组测试数据。每组输入两个正整数,表示游戏一开始的两个数,游戏总是小明先开始。
当输入两个0的时候,输入结束。
输出
对于每组输入,输出最后的胜者,我们认为他们两个都是顶尖高手,每一步游戏都做出了最佳的选择。
具体输出格式见输出样例。
样例输入
34 12
15 24
0 0
样例输出
xiaoming wins
xiaohong wins
两句话,能转移到必败点的是必胜点,只能转移到必胜点的是必败点。
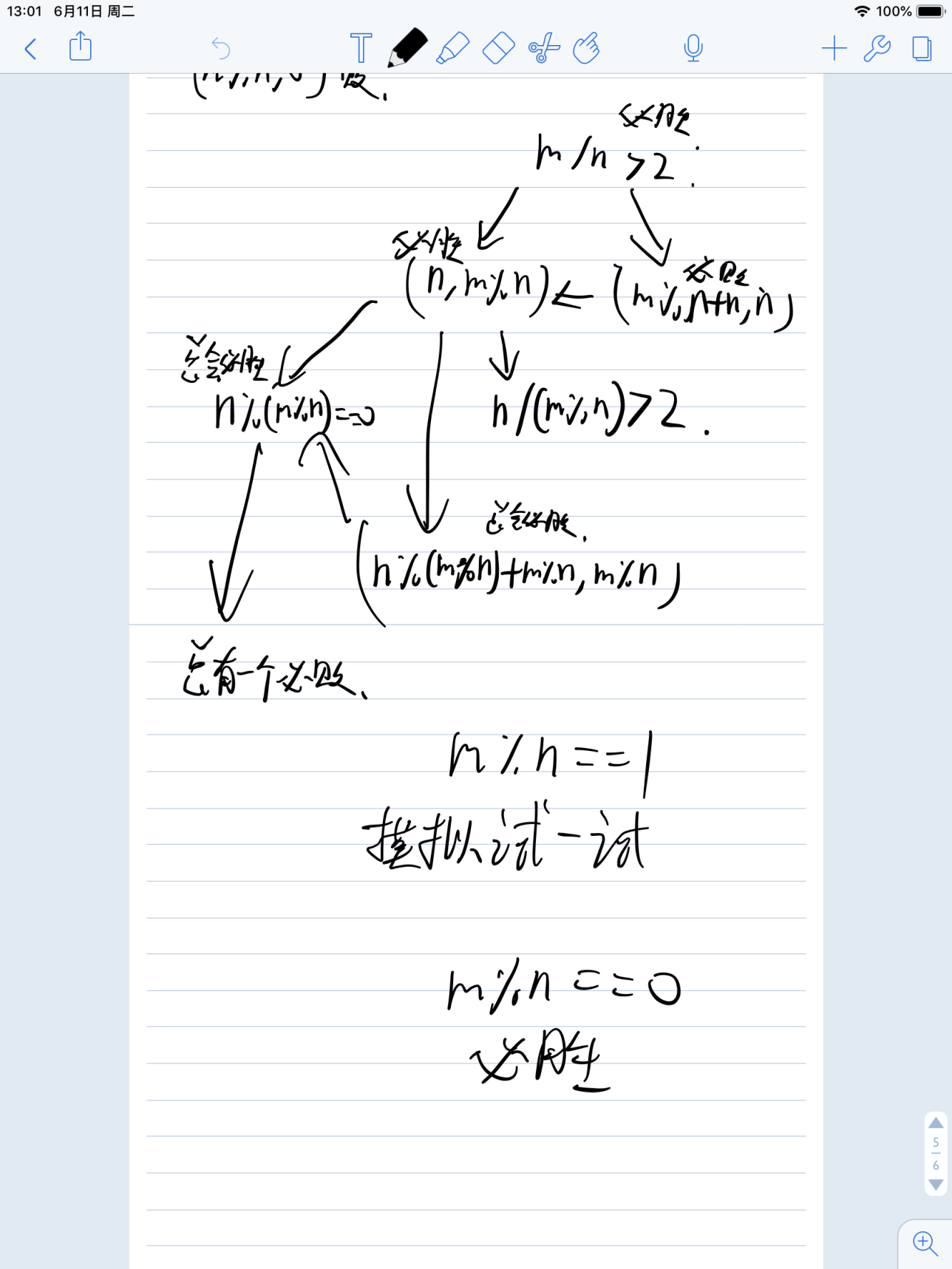
我是这么推出来的,或者从定理出发,一个点不是必败点就是必胜点,对三角形右下角分别假设,都可以推出m/n>2必胜
#include<cstdio>
#include<iostream>
#include<cstring>
#include<string>
#include<algorithm>
#define ll long long
using namespace std;
int n,m;
int main(){
while(scanf("%d%d",&n,&m)==2&&n&&m){
if(n>m) swap(n,m);
bool flag=true;
while(m%n!=0&&m/n==1){
m-=n;
if(n>m) swap(n,m);
flag=!flag;
}
if(flag){
printf("xiaoming wins
");
}
else printf("xiaohong wins
");
}
return 0;
}