原题链接:http://poj.org/problem?id=2826
一题很蛋疼的一题。目前为止还有一个问题我没搞清楚,问题注在代码中。
题目大意:
外面下雨了,农民Johnoson的bull(??是什么)Ben要接点雨水去浇花。Ben拿两个木板在墙上,如图所示,墙上的两块木板可以看作是空中的两条线段,它们有一定的宽度。
你的任务是计算两块木板能接多少水。
最后要计算两块木板能装水的部分的面积。但是要注意一种情况,雨是垂直往下滴的,如果装水的部分没有雨能够进去的话,也是接不到水的。如图:

这种情况下中间的部分虽然能装水,但是被上面的线段挡住了,雨也无法进入,这种情况下接水量是0。
思路分析:
首先排除几种情况:
1.两条线段如果不相交,则不可能产生存水的地方。
2.其中有一条线段是水平放置的,也不可能产生存水的地方。
3.如果两条线段在同一直线上,存水量也为0。
算法分析:
排除以上三种情况之后,存水量只与三点有关:线段的交点P,以及在P上面的点(y坐标大于P的y坐标的点)
设最高点为P0,次高点为P1。
过P1做竖直线和水平线,分别交P P0于点P2,P3。
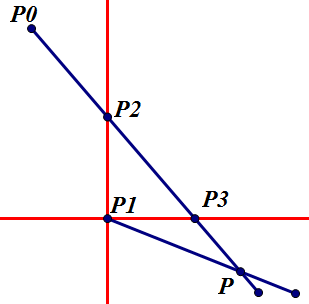
图1,被挡住的情况下,P2的y坐标必介于P0和P1之间。

图2,P2的y坐标大于P0的y坐标。雨可以进入。
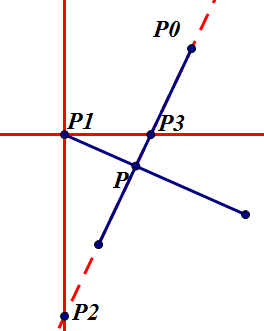
图3,P2 的y坐标小于P1的y坐标。
还有一种情况是没有交点。我的程序没有处理这种情况,但是也AC了。(出现这个情况的时候除数为0了,求出P2的坐标是(-1.#IND00,-1.#IND00)似乎表示无穷大?然后就不可能介于P0和P1之间了。。。)
最后如果是图1的情况输出0.00,否则计算三角形P,P1,P3的面积就是结果了。
附上代码:(纯C代码,略长。。。)

#include<stdio.h> #include<math.h> #define MAX(x,y) ((x)>(y)?(x):(y)) #define MIN(x,y) ((x)<(y)?(x):(y)) #define ABS(x) (((x)>0)?(x):(-(x))) #define EPS 0.0000001/*精度控制*/ /*坐标的定义*/ typedef double coo;/*int*/ /*判相等*/ int is_equel(double a,double b) { double c=ABS(a-b); if(c<=EPS) return 1;/*相等*/ else return 0;/*不相等*/ } /*点、向量*/ typedef struct POINT { coo x,y; }point,vector; /*线段*/ typedef struct SEGMENT { point p1,p2;/*p[2];*/ }segment,line; typedef struct LINE2/*一般式*/ { coo A,B,C; }line2; /*向量的减法p1-p2*/ vector vector_minus(vector p1,vector p2) { vector p; p.x=p1.x-p2.x; p.y=p1.y-p2.y; return p; } /*向量叉乘*/ double cross_product(vector p1,vector p2) {/*x1y2-x2y1*/ return p1.x*p2.y-p1.y*p2.x; } int line_location(line l1,line l2) { if((l2.p2.y-l2.p1.y)*(l1.p2.x-l1.p1.x)==(l1.p2.y-l1.p1.y)*(l2.p2.x-l2.p1.x)) { if((l2.p2.y-l1.p1.y)*(l1.p2.x-l1.p1.x)==(l1.p2.y-l1.p1.y)*(l2.p2.x-l1.p1.x)) return -1;/*重合*/ else return 1;/*平行*/ } else return 0;/*相交*/ } /*判断线段是否相交*/ int segment_intersect(segment l1,segment l2) { /*快速排斥试验*/ coo min,max; min=MIN(l1.p1.x,l1.p2.x); max=MAX(l2.p1.x,l2.p2.x); if(min>max) return 0; min=MIN(l2.p1.x,l2.p2.x); max=MAX(l1.p1.x,l1.p2.x); if(min>max) return 0; min=MIN(l1.p1.y,l1.p2.y); max=MAX(l2.p1.y,l2.p2.y); if(min>max) return 0; min=MIN(l2.p1.y,l2.p2.y); max=MAX(l1.p1.y,l1.p2.y); if(min>max) return 0; /*跨立试验*/ if(cross_product(vector_minus(l1.p1,l2.p1),vector_minus(l2.p2,l2.p1))*cross_product(vector_minus(l1.p2,l2.p1),vector_minus(l2.p2,l2.p1))>0) return 0; if(cross_product(vector_minus(l2.p1,l1.p1),vector_minus(l1.p2,l1.p1))*cross_product(vector_minus(l2.p2,l1.p1),vector_minus(l1.p2,l1.p1))>0) return 0; return 1; } line2 line_line2(line l) { line2 l2; l2.A=l.p2.y-l.p1.y; l2.B=l.p1.x-l.p2.x; l2.C=l.p2.x*l.p1.y-l.p1.x*l.p2.y; return l2; } /*直线相交的交点(两点式)*//*未处理平行和重合的情况*/ point line_intersection(line a,line b) { line2 l1,l2; point i={0,0}; l1=line_line2(a); l2=line_line2(b); i.x= (l2.B*l1.C-l1.B*l2.C)/(l2.A*l1.B-l1.A*l2.B); i.y=-(l2.A*l1.C-l1.A*l2.C)/(l2.A*l1.B-l1.A*l2.B); return i; } void scan(line *l) { scanf("%lf%lf%lf%lf",&l->p1.x,&l->p1.y,&l->p2.x,&l->p2.y); } int main() { int t,i,j; segment l1,l2; point P,p2; /*freopen("data.txt","r",stdin); freopen("ouput2.txt","w",stdout);*/ scanf("%d",&t); while(t--) { scan(&l1); scan(&l2); if(segment_intersect(l1,l2)==0) printf("0.00 "); else if(l1.p1.y==l1.p2.y||l2.p1.y==l2.p2.y) printf("0.00 "); else if(line_location(l1,l2)!=0) printf("0.00 "); else { point p[4]; P=line_intersection(l1,l2); p[0]=l1.p1; p[1]=l1.p2; p[2]=l2.p1; p[3]=l2.p2; for(i=1;i<4;i++) for(j=0;j<i;j++) { if(p[i].y>p[j].y) {p2=p[i];p[i]=p[j];p[j]=p2;} } { segment s1,s2,s0;/*| -*/ double S; s0.p1=p[0];s0.p2=P; s1.p1=p[1];s1.p2.x=p[1].x;s1.p2.y=p[1].y-1; s2.p1=p[1];s2.p2.x=p[1].x-1;s2.p2.y=p[1].y; p[2]=line_intersection(s1,s0); if(p[2].y<=p[0].y&&p[2].y>p[1].y) printf("0.00 "); else { p[3]=line_intersection(s2,s0); S=cross_product(vector_minus(p[1],P),vector_minus(p[3],P))/2; S=ABS(S); printf("%.2lf ",S+EPS);/*问题:为什么最后这里不加EPS就过不了呢???求大神解答。*/ } } } } return 0; }
不知道为什么调试过程中最后一步输出S之前已经取了绝对值,可是有次还是输出了-0.00。是什么情况???
