首先需要了解平面图的定义:
如果图 (G) 能画在平面 (S) 上,即 除顶点处外无边相交 ,则称 (G) 可平面嵌入 (S) , (G) 为可平面图或平面图。
设 (G) 是平面图,由 (G) 的边将 (G) 所在的平面划分成若干个区域,每个区域称为 (G) 的一个 面 ,其中面积无限的面称为无限面或外部面,面积有限的称为有限面或内部面。包围每个面的所有边组成的回路称为该面的 边界 ,边界的长度称为该面的 次数 。
为了强调平面图的面,用三元组表示一个平面图 (G=(V,E,F)) ,其中 (F) 表示平面图 (G) 中面的个数。
对于连通平面图,有欧拉公式:
[V-E+F=2
]
证明比较复杂,要涉及代数拓扑。
若 (G) 是连通的简单平面图(无重边与自环),则每个面的次数都 至少为 (3) ,又因为每条边仅属于 两个面 的边界,则有: (3F leq 2E) 。代入上式得:
[E leq 3V-6
]
然后再来看这道题。
输入中给出了这个图 (G) 和 (G) 中的一个哈密顿回路。
我们将这个哈密顿回路展开,即让其他边都在回路围成的区域内。
图为样例第一组数据:
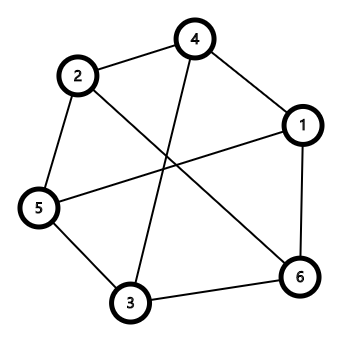
不难发现,上图中相交的两条边必须一条边在哈密顿回路内,一条在回路外才能不相交。
则问题转化为一个2-SAT问题,枚举相交的两条边 (i,j),连边:
- (i o j') 表示 (i) 在回路内则 (j) 必须在回路外。
- (j o i') 表示 (j) 在回路内则 (i) 必须在回路外。
- (i' o j) 表示 (i) 在回路外则 (j) 必须在回路内。
- (j' o i) 表示 (j) 在回路外则 (i) 必须在回路内。
缩点后判断是否存在 (i,i') 在同一个强连通分量中,若存在则 (G) 不是平面图。
然而 (M leq 10000) ,直接连边会爆炸。用上面的结论 (K leq 3V-6) 可以特判掉不可能成为平面图的情况。
( ext{Code}:)
#include <iostream>
#include <cstring>
#include <cstdio>
#include <algorithm>
#include <cmath>
#include <stack>
#define maxm 2000005
#define Rint register int
#define INF 0x3f3f3f3f
using namespace std;
typedef long long lxl;
template <typename T>
inline T read()
{
T x=0,f=1;char ch=getchar();
while(ch<'0'||ch>'9') {if(ch=='-') f=-1;ch=getchar();}
while(ch>='0'&&ch<='9') {x=(x<<1)+(x<<3)+ch-'0';ch=getchar();}
return x*f;
}
struct edge
{
int u,v,next;
inline bool operator < (const edge &T)const
{
return u<T.u||(u==T.u&&v<T.v);
}
}e[maxm],eg[10005];
int head[maxm],k;
inline void add(int u,int v)
{
e[k]=(edge){u,v,head[u]};
head[u]=k++;
}
int n;
int dfn[maxm],low[maxm],scc[maxm],dfs_cnt,scc_cnt;
stack<int> S;
inline void tarjan(int u)
{
S.push(u);
dfn[u]=low[u]=++dfs_cnt;
for(int i=head[u];~i;i=e[i].next)
{
int v=e[i].v;
if(!dfn[v])
{
tarjan(v);
low[u]=min(low[u],low[v]);
}
else if(!scc[v]) low[u]=min(low[u],dfn[v]);
}
if(dfn[u]==low[u])
{
int x;
++scc_cnt;
do
{
x=S.top();S.pop();
scc[x]=scc_cnt;
} while (x!=u);
}
}
int N,M,G[205];
inline void clear()
{
memset(head,-1,sizeof(head));
memset(dfn,0,sizeof(dfn));
memset(low,0,sizeof(low));
memset(scc,0,sizeof(scc));
k=scc_cnt=dfs_cnt=0;
}
int main()
{
// freopen("P3209.in","r",stdin);
int T=read<int >();
while(T--)
{
N=read<int >(),M=read<int >();
clear();
for(int i=1;i<=M;++i)
{
int u=read<int >(),v=read<int >();
eg[i]=(edge){u,v};
}
for(int i=1;i<=N;++i)
G[read<int >()]=i;
if(M>3*N-6) {puts("NO");continue;}
for(int i=1;i<=M;++i)
{
eg[i].u=G[eg[i].u];
eg[i].v=G[eg[i].v];
if(eg[i].u>eg[i].v) swap(eg[i].u,eg[i].v);
}
sort(eg+1,eg+M+1);
for(int i=1;i<M;++i)
for(int j=i+1;j<=M;++j)
if(eg[i].u<eg[j].u&&eg[j].u<eg[i].v&&eg[i].v<eg[j].v)// 判断是否相交
add(i+M,j),add(j+M,i),add(i,j+M),add(j,i+M);
for(int i=1;i<=(M<<1);++i)
if(!dfn[i]) tarjan(i);
bool flag=true;
for(int i=1;i<=M;++i)
if(scc[i]==scc[i+M])
{
flag=false;
break;
}
puts(flag?"YES":"NO");
}
return 0;
}