ML_regression

==================第一章=====================

After successfully completing this course, you will be able to use regression methods in practice, implement some of the most fundamental algorithms in this area, and choose the right model for your task. In addition, you will become proficient in core ML concepts that transcend regression settings: you will understand the practical implications of fundamental ML concepts, such as the bias-variance tradeoff, key ML data analysis techniques, such as cross validation, and the most important optimization techniques used to learn ML models, gradient descent and coordinate descent.

在实践中使用回归方法，实现一些最基本的算法，并选择合适的模型完成任务。

精通基本概念，如方差-偏差、最大似然、交叉验证、梯度下降和坐标下降等。

In this course, most of the assignments are about implementing algorithms from scratch。从零开始实现算法

小结：

本章学到了

==================第二章=====================

第一章是一个simple linear regression（简单的线性回归）

本章我们将consider "multiple regression" where multiple features of the data are used to form predictions（使用多个特征进行预测）
More specifically, in this module, you will learn how to build models of more complex relationship between a single variable (e.g., 'square feet') and the observed response (like 'house sales price'). This includes things like fitting a polynomial（多项式） to your data, or capturing seasonal changes in the response value. You will also learn how to incorporate multiple input variables (e.g., 'square feet', '# bedrooms', '# bathrooms'). You will then be able to describe how all of these models can still be cast within the linear regression framework, but now using multiple "features". Within this multiple regression framework, you will fit models to data, interpret estimated coefficients, and form predictions.Here, you will also implement a gradient descent algorithm for fitting a multiple regression model.

• how to build models of more complex relationship between a single variable (e.g., 'square feet') and the observed response (like 'house sales price'). 为输入输出构建复杂的模型
• how to incorporate multiple input variables使用多个特征
• describe how all of these models can still be cast within the linear regression framework, but now using multiple "features". 理解为什么这些模型仍可以称为线性回归。
• implement a gradient descent algorithm for fitting a multiple regression model实现梯度下降算法

~~~~开始啦~~~~

首先用预测房屋价格的例子开场，接着介绍回归的一些实际应用

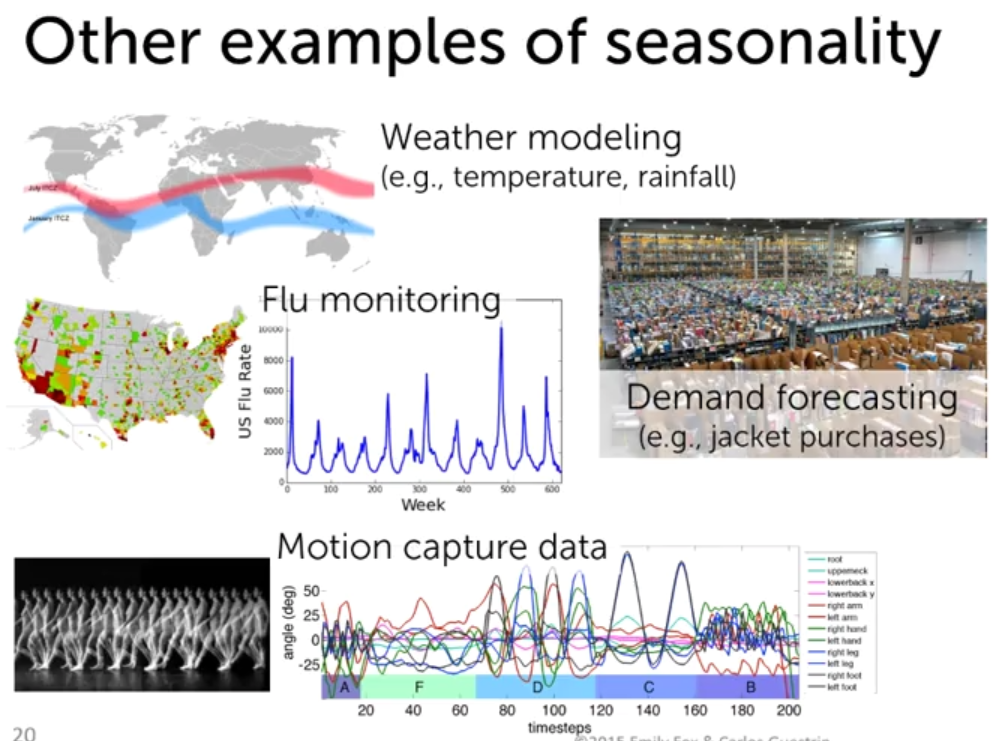
如图，天气预报、流感预测、商品需求预测等

我们可以看到这些都和季节性有关系，随着季节变化，天气、流感的感染率、商品的需求量、人体不同部位的运动量都有一些规律性的变化。比如会有一些流感高发季和低发季，可以引入三角函数；商品需求上，如冬天购买厚衣服，夏天需要半袖之类的等等

In this notebook you will use data on house sales in King County to predict prices using multiple regression. The first assignment will be about exploring multiple regression in particular exploring the impact of adding features to a regression and measuring error. In the second assignment you will implement a gradient descent algorithm. In this assignment you will:

• Use SFrames to do some feature engineering特征工程
• Use built-in GraphLab Create (or otherwise) functions to compute the regression weights (coefficients)计算回归权重（系数）
• Given the regression weights, predictors and outcome write a function to compute the Residual Sum of Squares计算RSS
• Look at coefficients and interpret their meanings解释系数和截断的意义
• Evaluate multiple models via RSS评估模型

第一章我们使用Graphlab实现了多项式回归，本章我们将使用SFrames和numpy用梯度下降来解得回归权重。

In this notebook we will cover estimating multiple regression weights via gradient descent. You will:

• Add a constant column of 1's to a SFrame (or otherwise) to account for the intercept
• Convert an SFrame into a numpy array。将一个SFrame转换成numpy数组
• Write a predict_output() function using numpy。用numpy实现函数predict_output()
• Write a numpy function to compute the derivative of the regression weights with respect to a single feature求导
• Write gradient descent function to compute the regression weights given an initial weight vector, step size and tolerance.实现梯度下降函数更新权重
• Use the gradient descent function to estimate regression weights for multiple features

==================第三章=====================

bias is the difference between this average fit and the true function, f true

经验风险最小化会可能带来过拟合

泛化误差从宏观上给出了算法的优劣评分

In this notebook you will compare different regression models in order to assess which model fits best. We will be using polynomial regression as a means to examine this topic. In particular you will:评估模型

• Write a function to take an an array and a degree and return an data frame where each column is the array to a polynomial value up to the total degree.
• Use a plotting tool (e.g. matplotlib) to visualize polynomial regressions
• Use a plotting tool (e.g. matplotlib) to visualize the same polynomial degree on different subsets of the data
• Use a validation set to select a polynomial degree
• Assess the final fit using test data

==================第四章=====================

In this assignment, we will run ridge regression(岭回归) multiple times with different L2 penalties to see which one produces the best fit. We will revisit the example of polynomial regression as a means to see the effect of L2 regularization. In particular, we will:

• Use a pre-built implementation of regression to run polynomial regression
• Use matplotlib to visualize polynomial regressions
• Use a pre-built implementation of regression to run polynomial regression, this time with L2 penalty
• Use matplotlib to visualize polynomial regressions under L2 regularization
• Choose best L2 penalty using cross-validation.
• Assess the final fit using test data.

==================第五章=====================

Which of the following statements about coordinate descent is true? (Select all that apply.)

A small enough step size should be chosen to guarantee convergence.

To test the convergence of coordinate descent, look at the size of the maximum step you take as you cycle through coordinates.

Coordinate descent cannot be used to optimize the ordinary least squares objective.

Coordinate descent is always less efficient than gradient descent, but is often easier to implement.

  

逆运算的复杂度

==================第六章=====================

limitations-of-parametric-regression参数回归的局限性

所以引出了最近邻方法，其中最简单的是1-nearest-neighbor-regression-approach1近邻回归方法　　

如何衡量远近？怎么样定义距离？在一维空间中我们采用欧式距离，在多维空间中有多种定义方法，最直接的是对不同维度进行加权计算

1-nearest-neighbor-algorithm1近邻算法

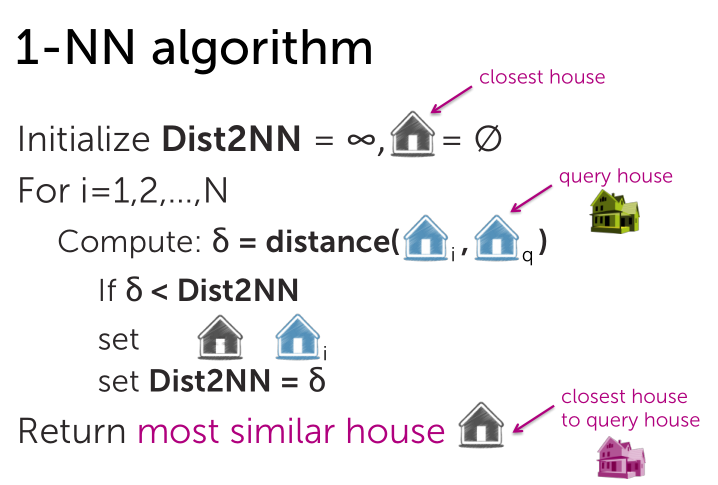
1近邻在数据量较少的情形下拟合效果不好，而且对噪音较为敏感。如果增加参考集数目，效果是否会有所改善呢？接下来我们讨论K近邻~

k-nearest-neighbors-in-practice K近邻的实际应用

　　Much more reasonable fit in the presence of noise在有噪数据集中拟合更合理

　　Boundary & sparse region issues

但是对于不连续数据集，整体上可能会有较高的精度，但对个体而言，还是有一些问题存在的。比如说我们都在某一领域内，但我在中心，你在边上，我们得到相同的分值，我就感觉不公平。对此，我们引出加权K近邻的方法~

Weigh more similar houses more than those less similar in list of k-NN与KNN列表中更相似的给予更高的权重

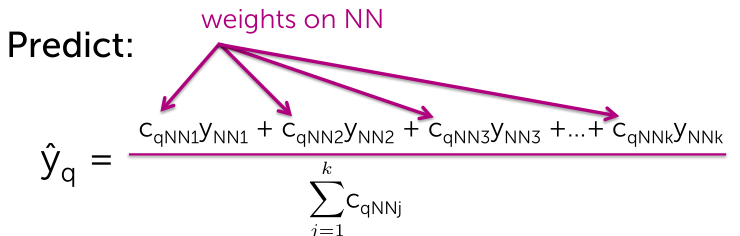
那如何定义权重呢？我们想让距离越大权重越小，距离越小权重越大。

Kernel regression（Instead of just weighting NN, weight all points）对所有点进行加权

 from-weighted-k-nn-to-kernel-regression

In this notebook, you will implement k-nearest neighbors regression. You will:

• Find the k-nearest neighbors of a given query input找出最近邻
• Predict the output for the query input using the k-nearest neighbors使用K近邻作预测
• Choose the best value of k using a validation set选择最优K

*****************************************************

　　　　　　　　　　　　　　小结

*****************************************************

simple-and-multiple-regression 

简单回归分析是simple regression was that we just had a single input and we're just fitting a very simple line as a relationship between the input and the output我们只是有一个单一的输入，我们用一个非常简单的线来拟合输入和输出之间的关系。然后我们对拟合结果进行评估，引出RSS，我们的目标是最小化RSS找到最好的拟合线。最后还讨论了拟合方程的两个变量（斜率和截距）

多项式回归分析是多个特征作为输入，还引入some epsilon term一些术语（eg噪音），介绍了the ridge regression岭回归， closed-form solution和gradient descent algorithm