78. 子集
Difficulty: 中等
给你一个整数数组 nums ,数组中的元素 互不相同 。返回该数组所有可能的子集(幂集)。
解集 不能 包含重复的子集。你可以按 任意顺序 返回解集。
示例 1:
输入:nums = [1,2,3]
输出:[[],[1],[2],[1,2],[3],[1,3],[2,3],[1,2,3]]
示例 2:
输入:nums = [0]
输出:[[],[0]]
提示:
1 <= nums.length <= 10-10 <= nums[i] <= 10nums中的所有元素 互不相同
Solution
子集系列题目的第一题,回顾先前回溯算法题目中提到的解题框架:
result = []
def backtrack(路径, 选择列表):
if 满足结束条件:
result.add(路径)
return
for 选择 in 选择列表:
做选择
backtrack(路径, 选择列表)
撤销选择
回答两个问题:1. 递归什么时候结束?2. 元素是可以被重复使用的还是不可以被重复使用的?
- 数组内每一个元素开头的子集都被找到之后回溯结束
- 可以被重复使用
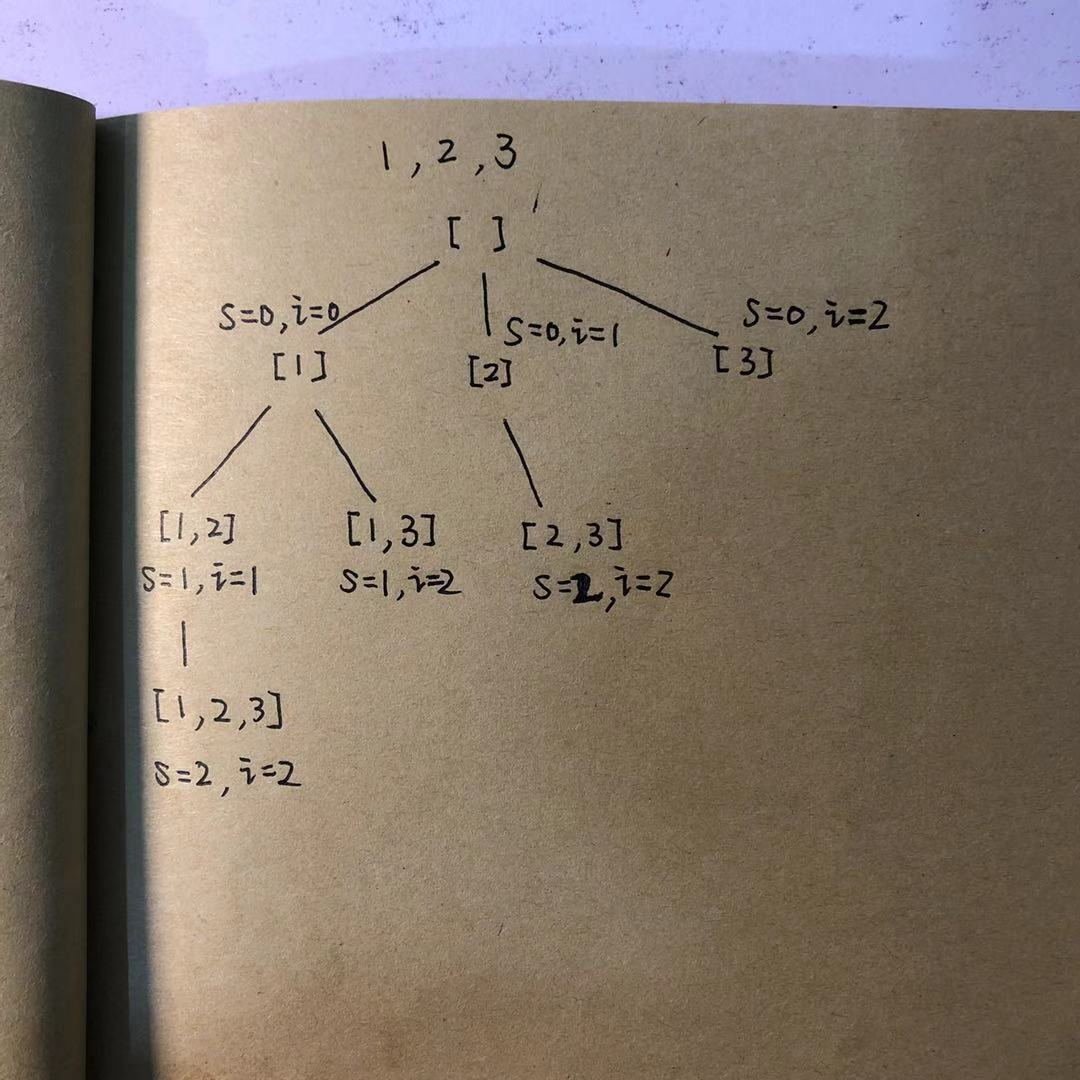
根据题意,这题实际上是一道组合combination问题,也就是每次从n个元素的数组中取0、1、···或者N个元素,有多少种组合结果。以下是回溯的过程,其实也是一个深度优先搜索的过程,s表示从数组的第s个元素开始循环。当s=0和i=0的时候表示从数组的第0个元素开始此时path为[1],往下递归,s=i+1=1表示从数组的第一个元素开始选择此时path为[1,2],然后pop退栈往上回到[1]的状态再向下递归,此时i已经加过1了,所以此时i为2,只能选择3了,此时的path为[1,3]
class Solution:
def subsets(self, nums: List[int]) -> List[List[int]]:
self.res = []
self.dfs(nums, 0, [], self.res)
return self.res
def dfs(self, nums, s, path, res):
res.append(path[:])
for i in range(s, len(nums)):
path.append(nums[i])
self.dfs(nums, i+1, path, res)
path.pop()