29. 两数相除
Difficulty: 中等
给定两个整数,被除数 dividend 和除数 divisor。将两数相除,要求不使用乘法、除法和 mod 运算符。
返回被除数 dividend 除以除数 divisor 得到的商。
整数除法的结果应当截去(truncate)其小数部分,例如:truncate(8.345) = 8 以及 truncate(-2.7335) = -2
示例 1:
输入: dividend = 10, divisor = 3
输出: 3
解释: 10/3 = truncate(3.33333..) = truncate(3) = 3
示例 2:
输入: dividend = 7, divisor = -3
输出: -2
解释: 7/-3 = truncate(-2.33333..) = -2
提示:
- 被除数和除数均为 32 位有符号整数。
- 除数不为 0。
- 假设我们的环境只能存储 32 位有符号整数,其数值范围是 [−231, 231 − 1]。本题中,如果除法结果溢出,则返回 231 − 1。
Solution
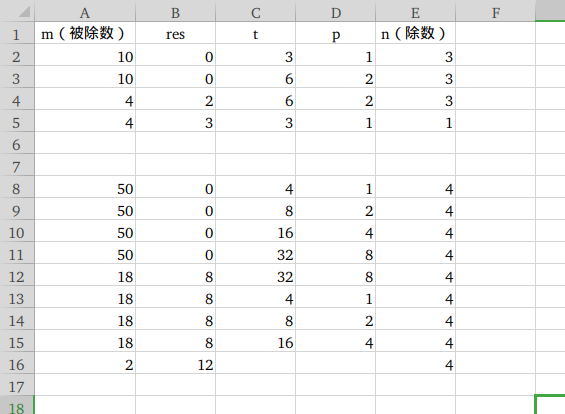
当被除数大于等于除数,进入如下循环,令t等于除数,m等于被除数,当m大于等于t的两倍时,t和p都增大一倍
class Solution:
def divide(self, dividend: int, divisor: int) -> int:
MIN, MAX = -2147483648, 2147483647
if (dividend == MIN and divisor == -1):
return MAX
# 除数和被除数取绝对值
m, n, res = abs(dividend), abs(divisor), 0
# 判断除数和被除数是否相同
sign = -1 if ((dividend < 0) ^ (divisor < 0)) else 1
if divisor == 1:
return m if sign == 1 else -m
while m >= n:
t = n
p = 1
while m >= (t << 1): # 如果m大于t的两倍
t <<= 1
p <<= 1
res += p
m -= t
return res if sign == 1 else -res