1.感知机模型
感知器模型只是适用于线性可分的二分类情况，例如有n个样本，x是n维的特征，y是二分标签{+1， -1}，任务是找到一条超平面将样本中的正负样本分开。
具体的，如果我们有m个样本，每个样本都对应与n为特征和一个二分类别输出，如下
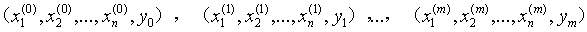
由输入空间到输出空间的函数为：
称为感知机，其中，w和b为感知机参数模型，w为一个n维行向量，叫做权值向量，b为一个标量，叫做偏置。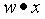
表示w和b的内积。sign是符号函数，即
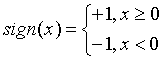
对于特征空间Rn中的一个超平面S，其中w是超平面的法向量，b是超平面的截距。这个超平面将特空间划分为两个部分，法向量指向的为正类，另外一类为负类。
2 感知机学习损失函数
感知器的目标是找到一个超平面将训练集的正负样本分开，只要确定了权值向量w和偏置b即确定了超平面，为了可以完成任务的超平面，就要确定一个学习策略，即定义一个损失函数并将损失函数最小化。
为了下面叙述方面，接下来做一个约定，即：
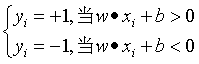
上面的公式的意思就是说，存在一个分离超平面，正例样本在超平面的上面，负例在超平面的下面。将上面两个公式合成一个公式，即：
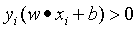
当存在错分的样本时，则错分的样本满足关系：
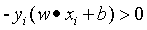
感知器的损失函数为误分类点到超平面S的总距离。
下面是某一个样本点x0到超平面的距离：
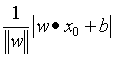
对于一个误分类的数据（xi, yi）来说，其到超平面S的距离是：
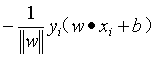
这样，假设超平面S的误分类点集合为M，那么所有误分类点到超平面S的总距离为：
当公式中分子的w扩大N倍时，公式的分母也会扩大N倍，因此可以固定分母为1，即将w和b同时缩小至w的二范数为1，这并不会改变超平。然后求分子的最小化作为损失函数，这样就得到了感知器的损失函数：
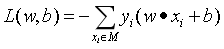
其中M为误分类点的集合。这个损失函数就是感知机学习的经验风险函数。
显然，损失函数L(w, b)是非负的，如果没有误分类点，损失函数值为0。而且，误分类点越少，误分类点离超平面越近，损失函数值就越小。
3 感知机学习算法
通过上一节的推导，得出感知机的损失函数，则感知机的学习问题变为求解损失函数的最优化问题，最优化的方法是随机梯度下降。
假如我们拥有m个样本，每个样本的特征维度为n的数据集，如下：
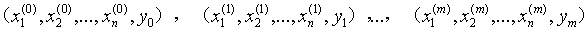
其中yi是一个二元类别输出+1或者-1，求参数w和b，使其为以下损失函数的极小化问题的解：
其中M为误分类点的集合。
感知机的损害函数只有和误分类的点有关，是误分类数据驱动的，具体采用随机梯度下降，首先先任意选择一个超平面w0，b0，然后用梯度下降法不断极小化目标函数，极小化的过程中不是一次是M中所有所有的误分类点的梯度下降，而是一次随机选取一个误分类点使其梯度下降。
加入误分类集合M是固定的，那么损失函数L(w,b)的梯度是：
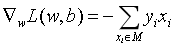
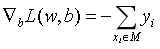
然后随机选取一个误分类点（xi, yi），接着对w和b进行更新：
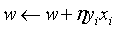
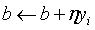
上式中，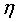
是学习率，又叫学习步长，是一个大于0，小于等于1的浮点值，这样就可以通过迭代是损失函数不断减小，直到算法收敛。
算法的执行步骤如下：
输入：线性可分的训练数据集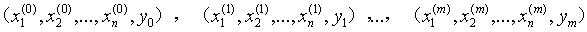
，其中y为二分类标签{+1， -1}， 学习率
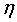(0 < 
<=1);
输出：w和b，感知机模型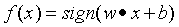
（1）选取初值w0，b0；
（2）在训练集中随机选取一个样本点（xi，yi）;
（3）如果
，
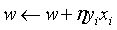
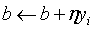
（4）转至(2), 直到训练集中没有误分类的点。
算法的直观解释：当一个样本点被误分类，即位于分离超平面的错误的一侧时，则调整w， b的值，使分离超平面想该误分类点的一侧移动，以减少该误分类点与超平面的距离，直到超平面越过该误分类点使其被正确分类。
4 感知机学习算法的对偶形式
在上一节算法中：
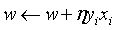
是对w和b进行逐个修改，即每一个循环迭代就只更新了一次，为了加速算法的收敛，设修改了n次，则w和b的增量为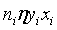
和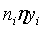
，其中ni的意思是通过样本点i修改了ni次w和b，这里可以令
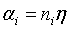。这样，从学习过程中就可以推导出最后学习到的w和b的值：
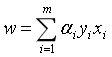
其中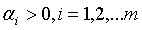
，m是样本的总量，当
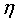=1时，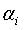
表示第i个样本由于误分类而进行更新的次数。样本点更新次数越多，意味着它距离分离超平面越近，也就越难正确分类。换句话说，这样的样本对学习的结果影响很大。
算法的执行步骤如下：
输入：线性可分的数据集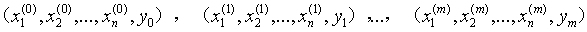
，其中y为二分类标签{+1， -1}， 学习率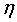(0 < <=1);
输出：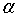
，b;感知机模型
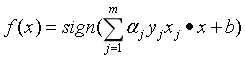，其中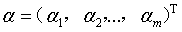
。
（1）
；
（2）在训练集中随机选取数据（xi, yi）;
（3）如果
，
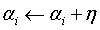
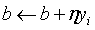（4）转至（2）直到没有误分样本数据。
（转载请注明出处，谢谢！）