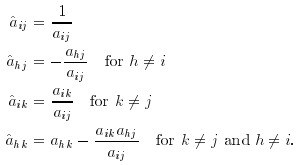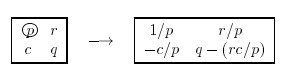某天我备考运筹学期间,找到了一份来自UCLA的讲义 ,考虑到考试需要以及和各种竞赛关系很大,决定好好学习一下。
讲义的 P4 给出了线性规划能解决的问题,标准最大化问题的形式:

简言之,要求你最大化 C1X1 + …… + CnXn,约束条件是下面的不等式,以及X为正。
以及标准最小化问题的形式:

接下来,他讲解了一些实际问题的例子,列成方程,都可以转化成标准最大化/最小化问题。
Goto Page 8: 里面给出了若干概念:
1:目标函数,就是咱们要最大/小化的函数
2:可行解(feasible vector),一个满足所有约束条件的向量(或者说X,Y)。
3:可行域,所有可行解的集合
4:最优解:顾名思义,一个可行的解,让目标函数取得最优值,就是最优解。
5:无解:可行域为空,没有可行解。这是线性规划问题解的一种特殊情况。
6:无界解:最优值可以取到无穷大,这是线性规划问题解的另一种特殊情况,
所有线性规划问题通过一些技巧都可以转化成标准形式。譬如不等式两边都 *= -1 变号。另一个情况就是变量 Xi 取值范围没有约束,可以列出等式 Xi = Xi_1 - Xi_2 代换掉所有的 Xi,然后给出约束 Xi_1 >= 0,Xi_2 >=0。 明白了概念之后,再看一看标准最小化/最大化问题,就可以一一对应了。
接下来,教材介绍了对偶。首先,他介绍了标准最大化问题和标准最小化问题互为对偶:

矩阵的形式看上去很抽象……画成表格看一下:

直观的多了,借助这个表格,也很容易可以计算得到一个问题的对偶。
看上去很Magic,补充一个实际问题来说明一下:
这是某个工厂的情况表,随手盗个图:

那么,对于工厂来讲,如果需要计算分别生产多少甲乙产品获利最大,那么很显然有:
Maximize 10X + 18Y
5X + 2Y <= 170
2X + 3Y <= 100
1X + 5Y <= 150
考虑另外一个问题:假设存在一个原料收购商人,他想要收购你的生产材料,他当然期望尽可能压价,设每样资源的单价为X,Y,Z
那么目标应该是:
Minimize 170X + 100Y + 150Z
但是工厂肯定期望收购价不低于自己生产的盈利,因此有约束条件:
5X + 2Y + 1Z >= 10
2X + 3Y + 5Z >= 18
这就是原问题和对偶问题为啥形式如此相近。
接下来,P11 Theorem 1: 弱对偶性。证明比较简单,因为 AX <= B && C’ <= Y’A ,所以 C'X <= Y'AX <= Y'B,去掉中间的,C'X <= Y'B
这个 Theorem 有什么意义呢,我们可以推出:
Corollary 1:如果原问题和对偶问题都可行,那么他们一定是有界可行。根据Theorem 1中的证明,如果对于标准最大化和最小化问题,分别存在着两个可行解 X,Y,那么最大化问题的解C'X一定小于最小化问题的解 Y’B,我们就找到了一个上界。因此,存在这样的上界。反之亦然。
Corollary 2:强对偶性,如果存在C’X* = Y*’B,则标准最大化最小化问题同时取得最优解。由于对任何最大化问题的可行解X,由Corollary 1,他都该小于等于Y*’B,而 Y*’B = C’X*,因此 C’X <= C’X*, 证明了X*已经是最优解。反之亦然。
因此有P11底端的对偶定理呼之欲出:如果原问题和对偶问题都是有解可行,那么一定存在一个解,让两个问题同时取得最优解。
结合上面的实际例子,这意味着,一定存在一个方案,恰好使工厂将材料卖出给收购商和自己生产取得收益相等。
之后解释了一下无解和无穷解的对偶关系,结论就是:对于线性规划问题,要么就是原问题和对偶问题都有解,要么就是都无解,要么就是无解和无穷解互为对偶,不存在其他情况。
接下来,咱们goto到第16页,学习一个Pivot操作
所谓Pivot,可以理解成换元,是把y’A = s’ 这个矩阵里面,用sj 和 y1...yi-1,yi+1... 表示yi,然后代入换元的操作。例子可见第16页。
直奔17页下方
这个式子给出了pivot操作之后,矩阵A 的变化,用矩阵的形式描绘就是
注意这个操作和求解线性规划无关,这只是一个很通用的对方程组的换元操作。
咱们研究这么个Pivot有什么用呢,goto Page 20,咱们试图来解这个标准最小化问题。
Y,A,B,C都好理解。原问题的约束条件是一个不等式组,我们加入松弛变量S将其转化成方程组,令S’ = Y’A - C’。
因此,咱们应该可以理解下面的那个单纯形表了。这个单纯形表表示的就是 S’ = Y’A - C’ 。
然后,这个问题怎么解呢,由于这个问题是标准最小化问题,容易知道,如果 B >= 0,-C >= 0,最优解应该是Y = 0,最优解也该 = 0,但是问题就是 B >= 0,-C >= 0这个条件不太好满足……因此,咱们的pivot操作就派上用场了,根据之前的变换规则,如果在一个位置 Aij 执行Pivot,交换 yi 和 sj ,那么会让 bi 和 cj 的值发生变化。如果之后满足了 B >= 0,-C >= 0,则相当于令 Y(当然这里的Y 可能一部分已经被S代换了)= 0,就得到了解。
接下来,他介绍了一个 Pivot Madly的方法,这可就看脸了……
而后,他介绍了一些策略。根据 Pivot 操作咱们知道,如果在位置 Ai,j Pivot,若Aij > 0, Bi >= 0,则Pivot之后,Aij,Bi 的正负一定不会变,而Cj的正负会反过来。 另一种情况,如果 Bi < 0,那么咱们如果可以找到一个 Aij < 0,那么就可以把Bi反过来。 就这样,不停Pivot,当 B 和 -C都 >= 0,即可得到最优解。最优解保存在这个矩阵的右下角。
这个实际上就是大名鼎鼎的单纯形法。如果我们从空间的角度上思考,每个约束条件,相当于是N维空间的一个超平面,限制这个超平面的一侧是解空间。那么若干个N维平面,他们相交会得到一个N+1个点的凸包,最优解一定是凸包的顶点,但是我们不知是哪个顶点。比起盲目枚举,单纯形法的本质就是从一个顶点出发,走向一个更优的相邻的顶点,直到走到最优解的过程。
由于匹配问题很容易可以转化成网络流问题,我们不单独讨论匹配问题。
我们讨论一下“最大流等于最小割”。
现在有一个网络,点 1->2,容量C1,流量F1;点 2->3,容量 C2,流量F2;点 1->3,容量C3,流量F3,源是1,汇是2,
根据流量平衡以及流量小于容量,我们可以列式:
Maximize 0F1 + 1F2 + 1F3
1F1 + 0F2 + 0F3 <= C1
0F1 + 1F2 + 0F3 <= C2
0F1 + 0F2 + 1F3 <= C3
1F1 - 1F2 + 0F3 <= 0
-1F1 +1F2 + 0F3 <= 0
而对偶问题则为:
Minimize C1X1 + C2X2 + C3X3 + 0X4 + 0X5
1X1 + 1X4 - 1X5 >= 0
1X2 - 1X4 + 1X5 >= 1
1X3 >= 1
易得 X3 >= 1,X1 + X2 >= 1,这就是对应的最小割问题。显然,1->3一定要割掉,1->2,2->3割哪一条,取决于C1,C2的大小了。