定理:设A,B为两个有限集,则(遇到这种问题画文氏图判断一下)
|AUB|=|A|+|B|-|AnB|.(并换成“或”,交换成“且”);
证明:见离散课本
例1:有多少个以”1“开始或者以”00“结尾的长度为8的0-1序列?
以”1”开始的长度为8的0-1序列有27=128个;
以“00”结尾的长度为8的0-1序列有26=64个;
以“1”开始且以“00”结尾的长度为8的0-1序列有128+64-32=160个
定理:设A,B,C是有限集合,则 |AUBUC|=|A|+|B|+|C|-| AnB|-|BnC|-|AnC|+|AnBnC|
(画一画文氏图)
证明:见离散课本
容斥原理进一步推广到m个有限集的计数问题上:
|A1UA2U...Am|
=∑mi=1|A1|-∑0≤i≤j≤m|AinAj|+∑0≤i≤j≤k≤m|AinAjnAk|+...+(-1)m-1|A1nA2n...nAm|;
错排问题:
问题:家中阳台有10盆不同的花,为保持新鲜感,希望每天重新摆放,使得每盆花都不在第一天放的位置。那么最多可以保持多少天每天摆法都不同?
抽象一下,若一个n元素的全排列中所有的元素都不在本来的位置上,那么称这个全排列就为原排列的一个错排(derangement).
问题:小明给n个朋友写信,邀请他们来家中聚会,结果粗心的他却把请柬全都装错了信封。请问有多少种全部装错信封的情况?
n个元素的错排的个数记为D(n)或d(n)或“!n",称作错排数或德·蒙特莫特数。
下边通过两种方法计算D(n)的具体值。
方法1:建立递推关系。
第一步,选择第n个元素的位置,共有n-1种方法(假定放在标号为k的位置);
第二步,选择第k个元素的位置,有两种可能
1.第k个元素放在标号为n的位置,此时剩下的n-2个元素进行错排即可,方案数是D(n-2);
2.第k个元素不在标号为n的位置,此时把标号为n的位置视作标号为k的位置,将(n-1)
个元素进行错排即可,方案数是D(n-1);
由此得到递推关系D(n)=(n-1)(D(n-2)+D(n-1)),初值D(1)=0,D(2)=1.
//推导过程
因为D(1)=0,则:0!=1,N(1)=0;
D(2)=1,则:2!=2*1,N(2)=1/2;
则N(1) = 0, N(2)=1/2.
n≥3时,
D(n-1)=(n-1)!*N(n-1),D(n-2)=(n-2)!*N(n-2);
则:n! N(n) = (n-1)*[ (n-1)! N(n-1) + (n-2)! N(n-2) ] ;
即 nN(n) = (n-1) N(n-1) + N(n-2) ;
则:[N(n)-N(n-1)] / [ N(n-1)-N(n-2)] =-1/ n;
[ N(n-1) - N(n-2) ] / [N(n-2)-N(n-3)] =-1/(n-1);
.
.
.
[ N[3] - N[2] ] / [ N[2]-N[1] =-1/3;
将上式累乘得:
于是有N(n) - N(n-1) = - [N(n-1) - N(n-2)] / n= (-1/n) [-1/(n-1)] [-1/(n-2)]…(-1/3) [N(2) - N(1)] = (-1)^n / n!.
因此
N(n-1) - N(n-2)= (-1)^(n-1) / (n-1)!,
…
N(2) - N(1) =(-1)^2 / 2!.
将上式累加,可得
N(n) = (-1)^2/2!+ … + (-1)^(n-1) / (n-1)! + (-1)^n/n!
因此
D(n) = n![(-1)^2/2! + … + (-1)^(n-1)/(n-1)! + (-1)^n/n!].
此即错排公式。//
方法二:应用容斥原理。
分别固定1个元素,2个元素...得到结果。
n个元素的全排列有n!个,用集合Ak表示第k个位置是第k个元素(也即元素k没有发生错排)的所有排列,则易得
|Ai|=(n-1)!,1≤i≤n
|AinAj|=(n-2)! 1≤i≤j≤n
......
|A1nA2n...nAn|=0!

不包含不动点(即错排数)的结果就是:
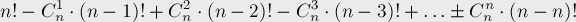
化简一下:
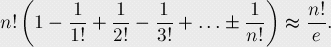
大佬博客,有关容斥原理的各种应用:
链接:https://www.cnblogs.com/fht-litost/p/9556802.html
百度百科关于错排问题:
链接:https://baike.baidu.com/item/%E9%94%99%E6%8E%92%E5%85%AC%E5%BC%8F/10978508?fr=aladdin