141. 环形链表
给定一个链表,判断链表中是否有环。
为了表示给定链表中的环,我们使用整数 pos 来表示链表尾连接到链表中的位置(索引从 0 开始)。 如果 pos 是 -1,则在该链表中没有环。
示例 1:
输入:head = [3,2,0,-4], pos = 1 输出:true 解释:链表中有一个环,其尾部连接到第二个节点。

示例 2:
输入:head = [1,2], pos = 0 输出:true 解释:链表中有一个环,其尾部连接到第一个节点。

示例 3:
输入:head = [1], pos = -1 输出:false 解释:链表中没有环。
思路l:让快指针走两步,慢指针走一步,只要有环,最后总会相遇

当一个链表有环时,快慢指针都会陷入环中进行无限次移动,然后变成了追及问题。想象一下在操场跑步的场景,只要一直跑下去,快的总会追上慢的。当两个指针都进入环后,每轮移动使得慢指针到快指针的距离增加一,同时快指针到慢指针的距离也减少一,只要一直移动下去,快指针总会追上慢指针。
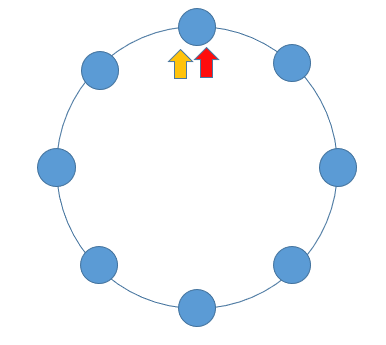

根据上述表述得出,如果一个链表存在环,那么快慢指针必然会相遇。实现代码如下:
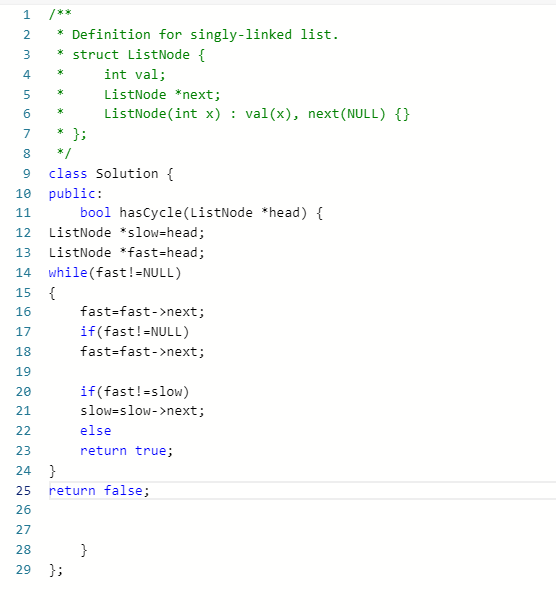
class Solution {
public:
bool hasCycle(ListNode *head) {
ListNode *slow = head;
ListNode *fast = head;
while(fast != nullptr) {
fast = fast->next;
if(fast != nullptr) {
fast = fast->next;
}
if(fast == slow) {
return true;
}
slow = slow->next;
}
return nullptr;
}
};
最后一个问题,如果存在环,如何判断环的长度呢?方法是,快慢指针相遇后继续移动,直到第二次相遇。两次相遇间的移动次数即为环的长度。
作者:Time-Limit
链接:https://leetcode-cn.com/problems/linked-list-cycle/solution/yi-wen-gao-ding-chang-jian-de-lian-biao-wen-ti-h-2/
来源:力扣(LeetCode)
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。