对于一类题目,是一棵树或者森林,有多次查询,求2点间的距离,可以用LCA来解决。
这一类的问题有2中解决方法。第一种就是tarjan的离线算法,还有一中是基于ST算法的在线算法。复杂度都是O(n);
先介绍在线算法:

1) dfs:
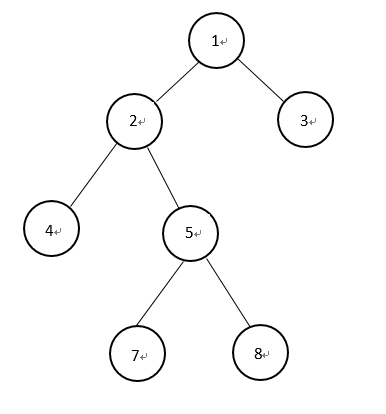
对于图所示的树,我们从根节点1开始dfs,按照先序访问(不算完全的先序),那么它访问顺序就是1 -> 2 -> 4 -> 2 -> 5 -> 7 -> 5 -> 8 -> 5 -> 2 -> 1 -> 3 -> 1
然后用数组first存第一次访问到该点时的时间(也就是访问顺序里面第一次访问到的下标)。 dfn[]存访问顺序对应的深度。
2) 初始化rmq:
根据节点的访问顺序初始化rmq,存的是这些访问顺序对应的深度的最小值对应的下标(也就是对应顺序里的下标)。
3)查询:
查询x,y的最近公共祖先。 令x = first[x],y = first[y],找到x和y第一次出现的位置,那么x,y的公共最近祖先一定也会在x,y之间出现,然后askrmq(x,y),这样就得深度最小的对应的公共祖先了。例如我们要找4,3的祖先,那么第一次出现3的对应下标是12,第一次出现4的下标是3,求3~12的最小深度对应的下标为11,也就是1节点。