完美正方形
如果一些边长互不相同的正方形,可以恰好拼出一个更大的正方形,则称其为完美正方形。历史上,人们花了很久才找到了若干完美正方形。比如:如下边长的22个正方形
2 3 4 6 7 8 12 13 14 15 16 17 18 21 22 23 24 26 27 28 50 60
如【图1.png】那样组合,就是一种解法。
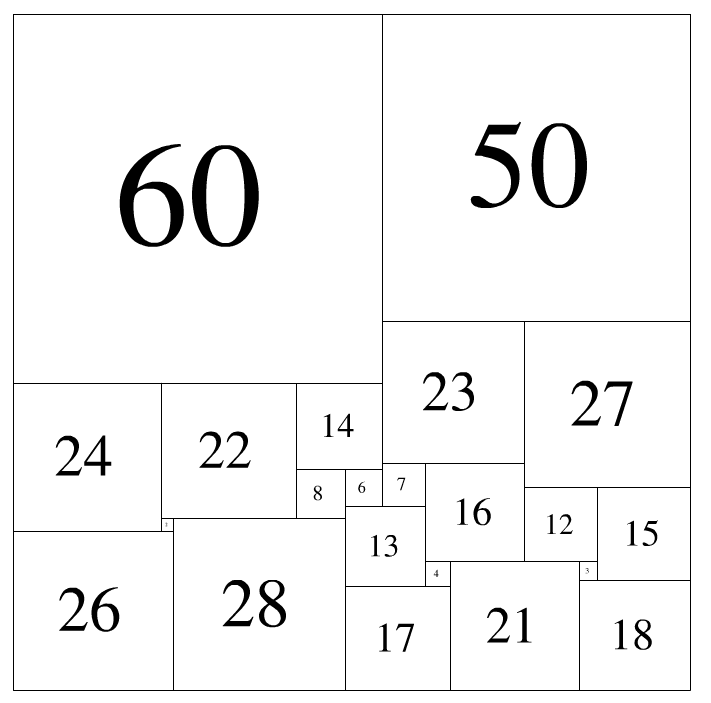
此时,紧贴上边沿的是:60 50,紧贴下边沿的是:26 28 17 21 18
22阶完美正方形一共有8种。下面的组合是另一种:
2 5 9 11 16 17 19 21 22 24 26 30 31 33 35 36 41 46 47 50 52 61
如果告诉你该方案紧贴着上边沿的是从左到右依次为:47 46 61,你能计算出紧贴着下边沿的是哪几个正方形吗?
请提交紧贴着下边沿的正方形的边长,从左到右,用空格分开。
不要填写任何多余的内容或说明文字。
解题思路:
既然已经给出紧贴着上边沿的三个正方形,便可以得知最终拼接成的大正方形边长为47+46+61=154我们将整个大正方形视为一个154*154的地图,将47 46 61三个正方形先拼到地图顶端。之后找到第一个空闲位置,深搜填入其他正方形,直到找到可以填满地图的填充方式为止。
1 #include <bits/stdc++.h> 2 using namespace std; 3 const int EDGE = 47 + 46 + 61; 4 //大正方形边长 5 int num[] = {2, 5, 9, 11, 16, 17, 19, 21, 22, 24, 26, 30, 31, 33, 35, 36, 41, 50, 52}; 6 //num需要是有序的 7 //记录剩下的所有可以被选取的正方形边长 8 int vis[20] = {false}; 9 //vis[i]记录i号正方形是否被选取过 10 int mp[EDGE][EDGE]; 11 //地图 12 void fillUp(int x, int y, int length, int fillNumber){ 13 //填充函数,x y为要填充位置的坐标(要填充正方形的左上角所在位置) 14 //length为填充正方形的长度,fillNumber表示填入地图的数字(填充时设为边长,拿出时设为0) 15 for(int i = x; i < x + length; i++) 16 for(int j = y; j < y + length; j++) 17 mp[i][j] = fillNumber; 18 } 19 bool isFull(){ //判断地图是否已被填满 20 for(int i = 0; i < EDGE; i++) 21 for(int j = 0; j < EDGE; j++) 22 if(!mp[i][j]) 23 return false; 24 return true; 25 } 26 bool judge(int x, int y, int length){ //判断位置x y是否能填入边长为length的正方形 27 if(x + length > EDGE || y + length > EDGE) 28 return false; 29 for(int i = x; i < x + length; i++) 30 for(int j = y; j < y + length; j++) 31 if(mp[i][j]) 32 return false; 33 return true; 34 } 35 bool dfs(int x, int y){ 36 if(isFull()) //如果地图已被填满则找到答案,返回true 37 return true; 38 if(x > EDGE || y > EDGE) 39 return false; 40 bool flag = false; 41 int newX, newY; 42 for(int i = 0; i < EDGE; i++){ //将newX newY记录为地图上第一个空位的坐标 43 for(int j = 0; j < EDGE; j++) 44 if(!mp[i][j]){ 45 newX = i, newY = j; 46 flag = true; 47 break; 48 } 49 if(flag) 50 break; 51 } 52 for(int i = 0; i < 19; i++){ 53 if(judge(newX, newY, num[i])){ //位置newX newY能填入边长为num[i]的正方形 且边长为num[i]的正方形还没有被选取过 54 if(!vis[i]){ 55 fillUp(newX, newY, num[i], num[i]); //将长度为num[i]的正方形 填入位置 newX, newY 56 vis[i] = true; //边长为num[i]的正方形标记为已选取 57 if(dfs(newX, newY + num[i])) 58 return true; 59 fillUp(newX, newY, num[i], 0); //将长度为num[i]的正方形从位置 newX, newY取出 60 vis[i] = false; //边长为num[i]的正方形标记为未选取 61 } 62 }else //由于num是有序的只要num[i]无法放入位置newX newY则之后的正方形都无法放入位置newX newY 63 break; 64 } 65 return false; 66 } 67 int main() 68 { 69 fillUp(0, 0, 47, 47); 70 fillUp(0, 47, 46, 46); 71 fillUp(0, 93, 61, 61); 72 //将题中给出的上方三个正方形填入地图 73 dfs(0, 0); 74 //int ans = 0; 75 for(int j = 0; j < EDGE; j++) 76 printf("%3d ", mp[153][j]); //打印最后一行 77 return 0; 78 }
答案:
50 33 30 41