前言:希望自己每個星期能發一篇文章,提升一下寫文章的能力?雖然對語文作文毫無幫助但是總比玩遊戲強
所以不務正業的東西就不放在首頁了,有興趣的可以點分類去看
來源:https://www.cnblogs.com/COLIN-LIGHTNING/p/8450053.html 以及書
1.遞推公式:
(1)一般:c [ n ]=Σ c [ k ] * c [ n-k-1 ],邊界為c[ 0 ]=1
其遞推解為c [ n ]=C( 2n,n ) / ( n+1 ),即通項公式,其中C表示組合數。
化簡得c [ n ]=2n*( 2n-1 ).....( n+2 ) / n!
(2)另類遞推式:c [ n ]=c[ n-1 ] * ( 4n-2 ) / ( n+1 ),邊界為c [ 0 ]=1
其遞推解為c [ n ]=C(2n,n)-C(2n,n-1)
(3)其他公式:c [ n ]=( Σ ( 0<=i<=n ) C( i,n )^2 ) / ( n+1 )
通過展開可發現它們的本質是一樣的。
2.這裡看一下它們的用處:(來自P1044 棧 題解)
(1)c [ n ]=Σ c [ k ] * c [ n-k-1 ]
在數據一大的情況下就比較麻煩
(2)c [ n ]=c[ n-1 ] * ( 4n-2 ) / ( n+1 )
對於大數據要mod一個數的時候,難保一個f [ n ]%mod=0
那麼根據公式下面所有的數都會等於0,非常的不好
(3)組合數公式1:c [ n ]=C( 2n,n ) / ( n+1 )
組合數是一個楊輝三角可以通過遞推得到,但是對大數據取膜模的時候並不滿足取模的性質的(但是可以用逆元?),所以也會比較麻煩
(4)組合數公式2:c [ n ]=C(2n,n)-C(2n,n-1)
與組合數公式1不同的是這是兩個組合數相減的形式,可以用模的性質,這樣就比較好
所以很多情況下我們可以用(4)的公式。
3.简单应用
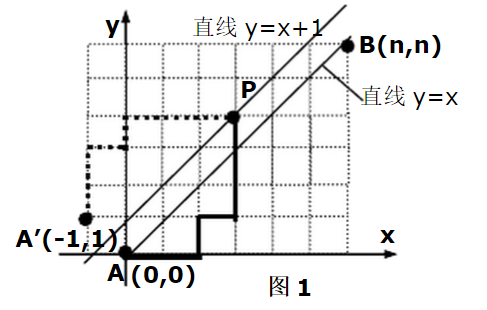
(1)求解路径方案数:如图所示,从原点(0,0)到点B(n,n),只能向右或向上进行长度为一个单位的移动,路线一直处于y=x之下(不越过直线y=x)的不同路径方案数;
Solution:每个n的解都可以看做先前的解数(再向右向上即为所求)加上不触及各个y=x上的点到达B点的方案数,可以发现其递推公式即为卡特兰数计算公式;
(2)求01串的个数:n个0与n个1构成的序列方案数,使得任何一个前缀0的个数不少于1的个数;
Solution:将0看做在坐标系中向右走一步,1看做向上走一步,则问题可化简为从原点到(n,n)所有路线中一直处于y=x之下(不越过直线y=x)的不同路径方案数,与上题相同,方案数即为对应n的卡特兰数;
(3)给定节点求解二叉树的个数:已知由n个节点,求形成不同的二叉树有多少种?
Solution:将向左生成子树看做0,向右生成字数看成1,则问题化简为求n/2个0和n/2个1构成数串的不同方案数,即上题无条件解的一半,与上题答案相同,形成不同的树的个数即为对应n的卡特兰数;
(4)求凸边形进行三角剖分的不同方案数:在一个有n+3条边的凸多边形中,求通过若干条互不相交的对角线,把这个多边形划分成若干个三角形的不同方案数。
Solution:因为每一条边都一定是剖分后的三角形的一条边,任意一条边都会把多边形分成两个小多边形,那么根据乘法原理,解即为划分成不同多边形的方案数对应小多边形的划分方案数之和,即f[n]=Σ(3≤k≤n-3)f[k]f[n-k-1],可以发现解数即为n对应的卡特兰数;
(5)n对括号正确匹配数目:给定n对括号,求括号正确配对的字符串数;
Solution:因为是匹配问题,那么最后一个左括号必然有唯一右括号与其匹配,假设f[n]为n对括号的正确配对数目,那么有递推关系f[n]=f[0]f[n-1]+f[1]f[n-2]+...+f[n-1]f[0],显然f[n]是n对应的卡特兰数。
4.卡特兰数的扩展(折线原理)
对于在n位的2进制中,有m个0,其余为1的catalan数为:C(n,m)-C(n,m-1)。其可由应用(1)证明;
例題:
1.luogu P1044 棧
可以將n個數分成兩部分,一部分入棧出棧的方案數和另一部分的入棧出棧方案數滿足乘法原理,
也就是 f [ i ]=Σ f [ j ](前一部分)*f [ i-j-1 ](后一部分)(1<=i<=n,0<=j<i)
剛好是卡特蘭數,數據較小,公式(1)暴力遞推即可
也有二維動態規劃的解法,f [ i ] [ j ]表示 i 個在棧里,j 個在棧外,
每次兩種選擇:出棧或入棧 於是 f [ i ] [ j ]=f [ i-1 ] [ j ]+ f [ i ] [ j-1 ] 好像就是卡特蘭數的方法
邊界:f [ i ] [ 0 ]=1 ( 0<=i<=n )
2.luogu P1976 雞蛋餅
這里的圓和多邊形沒有什麼本質區別,所以和引用中的(4)一樣,直接求卡特蘭數即可
這個數據範圍仍然不大,所以還用公式(1)每次取膜就可以,注意乘的時候要轉longlong,會爆int
會繼續更新(有生之年)