二叉树【基础算法题】

题目一

 思路

1）递归

忽略打印，实际上递归节点到达每个节点的顺序如图。打印的时机放到第一行就是先序遍历，打印的时机放到第二行就是中序遍历，打印的时机放到第三行就是后序遍历。

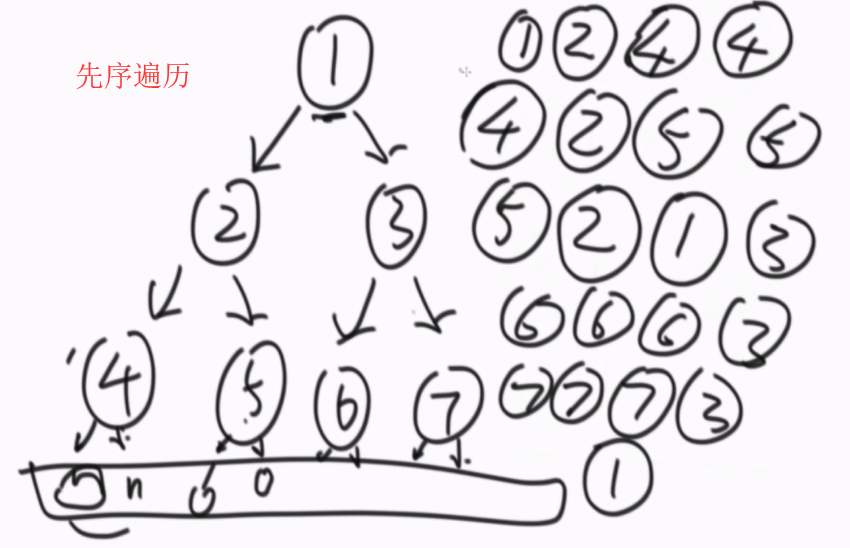
先序遍历：根节点→左子树→右子树。按照忽略打印实际递归顺序每个数第一次出现的顺序。1 2 4 5 3 6 7

中序遍历：左子树→根节点→右子树。按照忽略打印实际递归顺序每个数第二次出现的顺序。4 2 5 1 6 3  7

后续遍历：左子树→右子树→根节点。按照忽略打印实际递归顺序每个数第三次出现的顺序。4 5 2 6 7 3 1

2）非递归

自己准备一个栈。

先序遍历

1 2 4 5 3 6 7  中左右

如果头结点为空不打印，如果不为空压入栈中，进入while循环。

如果栈不为空，将栈中栈顶节点出栈并打印。如果当前节点右孩子不为空则将其压入栈中，如果当前节点左孩子不为空则将其压入栈中。

···以此类推，不断循环这个过程，直到所有节点都遍历完。

步骤：

1 压栈

1 出栈 打印

3 压栈 2压栈

2 出栈 打印

5 压栈 4 压栈

4 出栈 打印

5 出栈 打印

3 出栈 打印

7 压栈 6 压栈

6 出栈 打印

7 出栈 打印

中序遍历

4 2 5 1 6 3  7 左中右

如果头结点为空什么都不做，如果不为空，准备好一个栈。

如果栈不为空，或者头结点不为空，进入while循环。

如果当前节点不为null，会把自己压栈，当前节点向左移动。

如果当前节点为null，栈顶元素出栈并打印，当前节点向右移动。

···以此类推，不断循环这个过程，直到所有节点都遍历完。

步骤：

1 压栈 2压栈 4压栈

当前节点到了4的左孩子 为null

4 出栈 打印

当前节点到了4的右孩子 为null

2 出栈 打印

当前节点到了2的右孩子 不为null

5 压栈

当前节点到了5的左孩子 为null

5 出栈 打印

当前节点到了5的右孩子 为null

1 出栈 打印

当前节点到了1的右孩子 不为null

3 压栈

当前节点到了3的左孩子 不为null

6 压栈

当前节点到了6的左孩子 为null

6 出栈 打印

当前节点到了6的右孩子 为null

3 出栈 打印

当前节点到了3的右孩子 不为null

7 压栈

当前节点到了7的左孩子 为null

7 出栈 打印

当前节点到了7的右孩子 为null

此时栈空，退出循环，遍历结束。

后序遍历

4 5 2 6 7 3 1 左右中

方法一：准备两个栈，根据先序遍历的中左右，调整为中右左的顺序，将这个顺序压入另一个栈中，依次出栈的顺序就是左右中了。

方法二：使用一个栈。

代码实现

package class_04;

import java.util.Stack;

public class Code_01_PreInPosTraversal {

    public static class Node {
        public int value;
        public Node left;
        public Node right;

        public Node(int data) {
            this.value = data;
        }
    }

    public static void preOrderRecur(Node head) {//递归先序
        if (head == null) {
            return;
        }
        System.out.print(head.value + " ");
        preOrderRecur(head.left);
        preOrderRecur(head.right);
    }

    public static void inOrderRecur(Node head) {//递归中序
        if (head == null) {
            return;
        }
        inOrderRecur(head.left);
        System.out.print(head.value + " ");
        inOrderRecur(head.right);
    }

    public static void posOrderRecur(Node head) {//递归后序
        if (head == null) {
            return;
        }
        posOrderRecur(head.left);
        posOrderRecur(head.right);
        System.out.print(head.value + " ");
    }

    public static void preOrderUnRecur(Node head) {//非递归先序
        System.out.print("pre-order: ");
        if (head != null) {
            Stack<Node> stack = new Stack<Node>();
            stack.add(head);
            while (!stack.isEmpty()) {
                head = stack.pop();
                System.out.print(head.value + " ");
                if (head.right != null) {
                    stack.push(head.right);
                }
                if (head.left != null) {
                    stack.push(head.left);
                }
            }
        }
        System.out.println();
    }

    public static void inOrderUnRecur(Node head) {//非递归中序
        System.out.print("in-order: ");
        if (head != null) {
            Stack<Node> stack = new Stack<Node>();
            while (!stack.isEmpty() || head != null) {
                if (head != null) {
                    stack.push(head);
                    head = head.left;
                } else {
                    head = stack.pop();
                    System.out.print(head.value + " ");
                    head = head.right;
                }
            }
        }
        System.out.println();
    }

    public static void posOrderUnRecur1(Node head) {//非递归后序
        System.out.print("pos-order: ");
        if (head != null) {
            Stack<Node> s1 = new Stack<Node>();
            Stack<Node> s2 = new Stack<Node>();
            s1.push(head);
            while (!s1.isEmpty()) {
                head = s1.pop();
                s2.push(head);
                if (head.left != null) {
                    s1.push(head.left);
                }
                if (head.right != null) {
                    s1.push(head.right);
                }
            }
            while (!s2.isEmpty()) {
                System.out.print(s2.pop().value + " ");
            }
        }
        System.out.println();
    }

    public static void posOrderUnRecur2(Node h) {
        System.out.print("pos-order: ");
        if (h != null) {
            Stack<Node> stack = new Stack<Node>();
            stack.push(h);
            Node c = null;
            while (!stack.isEmpty()) {
                c = stack.peek();
                if (c.left != null && h != c.left && h != c.right) {
                    stack.push(c.left);
                } else if (c.right != null && h != c.right) {
                    stack.push(c.right);
                } else {
                    System.out.print(stack.pop().value + " ");
                    h = c;
                }
            }
        }
        System.out.println();
    }

    public static void main(String[] args) {
        Node head = new Node(5);
        head.left = new Node(3);
        head.right = new Node(8);
        head.left.left = new Node(2);
        head.left.right = new Node(4);
        head.left.left.left = new Node(1);
        head.right.left = new Node(7);
        head.right.left.left = new Node(6);
        head.right.right = new Node(10);
        head.right.right.left = new Node(9);
        head.right.right.right = new Node(11);

        // recursive
        System.out.println("==============recursive==============");
        System.out.print("pre-order: ");
        preOrderRecur(head);
        System.out.println();
        System.out.print("in-order: ");
        inOrderRecur(head);
        System.out.println();
        System.out.print("pos-order: ");
        posOrderRecur(head);
        System.out.println();

        // unrecursive
        System.out.println("============unrecursive=============");
        preOrderUnRecur(head);
        inOrderUnRecur(head);
        posOrderUnRecur1(head);
        posOrderUnRecur2(head);

    }

}

题目二

 思路

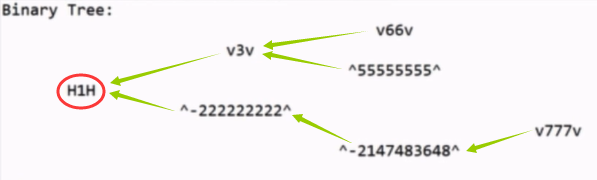
H*H是头结点*。

v*v是代表*的父节点是左下方离*最近的。

^*^是代表*的父节点是左上方离*最近的。

   

代码实现

直观打印二叉树

题目三

思路

每个节点都能通过它的parent指针找到它的父节点；头结点的父指针指向自己或null，大多情况都设置为null。

 在中序遍历的序列中，一个节点的下一个节点（后继节点）是它的父节点。

 

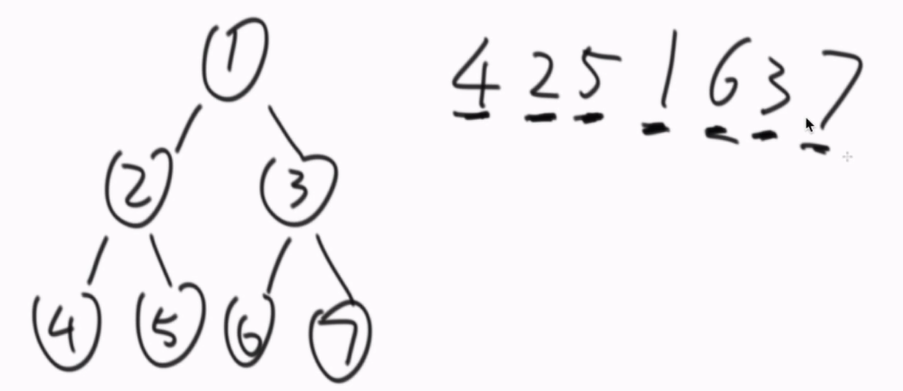
 例：如果只给了其中一个节点，可以通过它的parent指针，一路找到头结点，再从头结点进行中序遍历，这样就能找到所有节点的父节点，但是这样要遍历整颗树，复杂度较高。

怎么能不遍历整颗树也能找到某节点的父节点呢？

在中序遍历序列中，

①一个节点，只要其有右子树，那它的后继节点一定是它的整颗右子树中最左的那个节点。

②一个节点x，若其没有右子树，要考察到底那个节点作为其整颗左子树的最后一个节点。如果没有就是不存在。例如节点7没有后继节点。

(通过x的parent指针往上找，如果x是它父节点的右孩子，继续往上找，当前节点变为x的父节点，直到当前节点是当前节点的父节点的左孩子停止，当前节点的父节点就是x的后继节点，如果某一步parent是空，则表示x没有后继节点。)

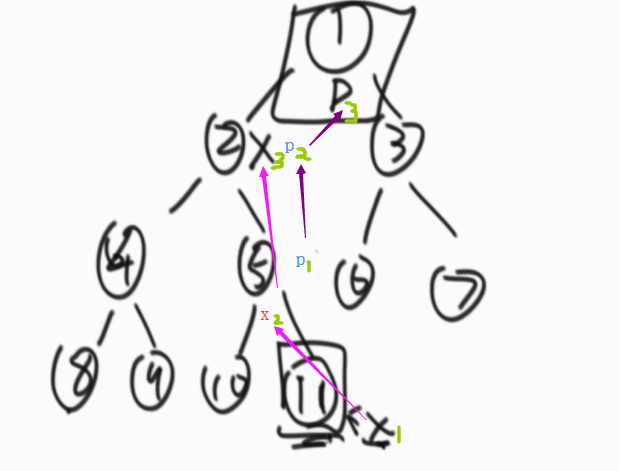         11的后继是1

举一反三：怎么找一个节点的前驱节点?

①一个节点，只要其有左子树，那它的前驱节点一定是它的整颗左子树中最右的那个节点。

②一个节点x，若其没有左子树，通过x的parent指针往上找，如果x是它父节点的左孩子，继续往上找，当前节点变为x的父节点，直到当前节点是当前节点的父节点的右孩子停止，当前节点的父节点就是x的前驱节点，如果某一步parent是空，则表示x没有前驱节点。

代码实现

查找二叉树中某个节点的后继节点

题目四

 思路

在内存里可以串起一棵树，但关机的时候，内存里的东西就销毁了，怎么能把它变成文件的形式记录下来，以便能把树重建？

把内存中的树记录下来的过程就叫序列化，重建树（还原内存中树结构）的过程就叫反序列化。

【方法一】

先序的方式序列化

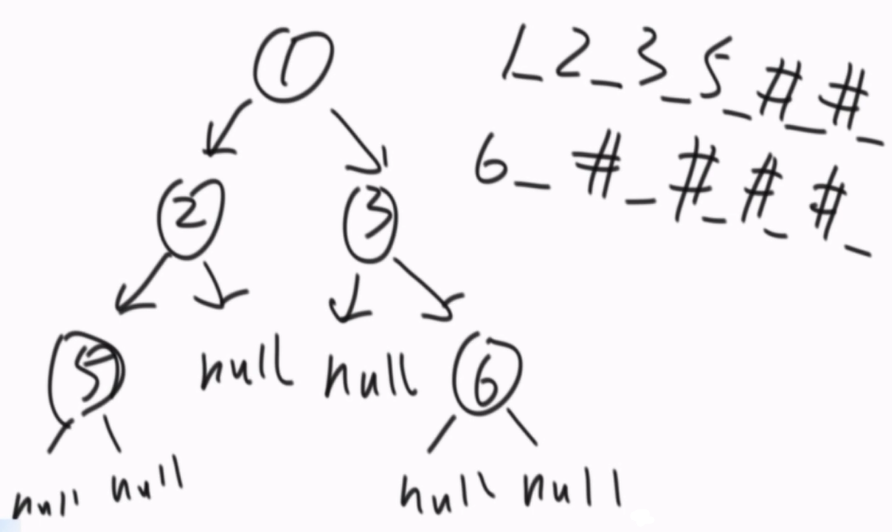
按照先序遍历得到的顺序来组成一个字符串，存储起来，每个节点后有一个下划线（用于隔开各个节点），当前节点为null时，用#代替节点。

加上空是为了区分结构（当节点的值相等时，会存在它的先序中序后序是一样的的情况）。

先序的方式反序列化

怎么序列化就怎么反序列化。

第一个数是根节点，依次按先序顺序（中左右）来建立树，当前节点x为null时，不再继续往下，当前节点x回到它的父节点y，再走到y的右孩子，当遍历过右孩子后，继续往上走，以此类推，直到所有节点都建立完毕。

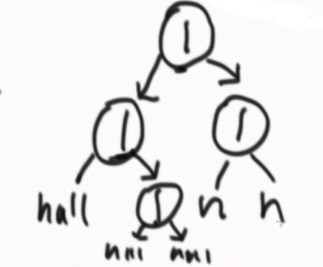
中序和后序遍历的序列化和反序列化类似。

【方法二】

按层序列化

代码实现

序列化代码

题目五

 代码实现

 折纸代码

题目六

 思路

平衡二叉树：对于一颗二叉树中的任何节点，它的左右子树的高度差不超过1。满二叉树一定时平衡二叉树，但平衡二叉树不一定是满二叉树。平衡性主要是用来解决效率问题的。

如果树中以每一个节点作为头结点的树都是平衡树，则整棵树是平衡的。

1）左树是否平衡，左树不平衡直接返回false。

2）左树平衡了，右树是否平衡？右树不平衡返回false。

3）左树和右树都平衡，左树的高度是几？右树的高度是几？

4）判断左树和右树的高度差，即可判断出整棵树是否平衡。

由以上分析可知，我们的递归函数需要返回两个信息，当前树是否是平衡的，以及这棵树的高度。

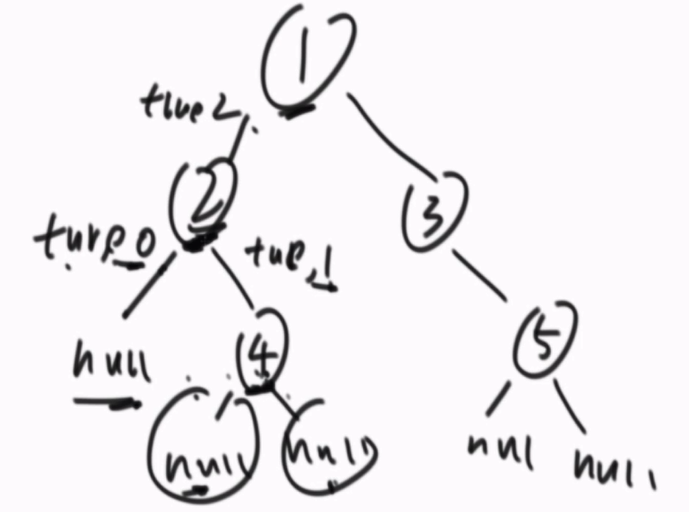
关键词：树形BP

代码实现

package class_04;

public class Code_06_IsBalancedTree {

    public static class Node {
        public int value;
        public Node left;
        public Node right;

        public Node(int data) {
            this.value = data;
        }
    }

    public static boolean isBalance(Node head) {
        boolean[] res = new boolean[1];
        res[0] = true;
        getHeight(head, 1, res);
        return res[0];
    }

    public static int getHeight(Node head, int level, boolean[] res) {
        if (head == null) {
            return level;
        }
        int lH = getHeight(head.left, level + 1, res);
        if (!res[0]) {
            return level;
        }
        int rH = getHeight(head.right, level + 1, res);
        if (!res[0]) {
            return level;
        }
        if (Math.abs(lH - rH) > 1) {
            res[0] = false;
        }
        return Math.max(lH, rH);
    }

    public static void main(String[] args) {
        Node head = new Node(1);
        head.left = new Node(2);
        head.right = new Node(3);
        head.left.left = new Node(4);
        head.left.right = new Node(5);
        head.right.left = new Node(6);
        head.right.right = new Node(7);

        System.out.println(isBalance(head));

    }
}

题目七

 思路

搜索二叉树：对于树中任意一个节点x为头的子树，左子树都比x小，右子树都比x大。

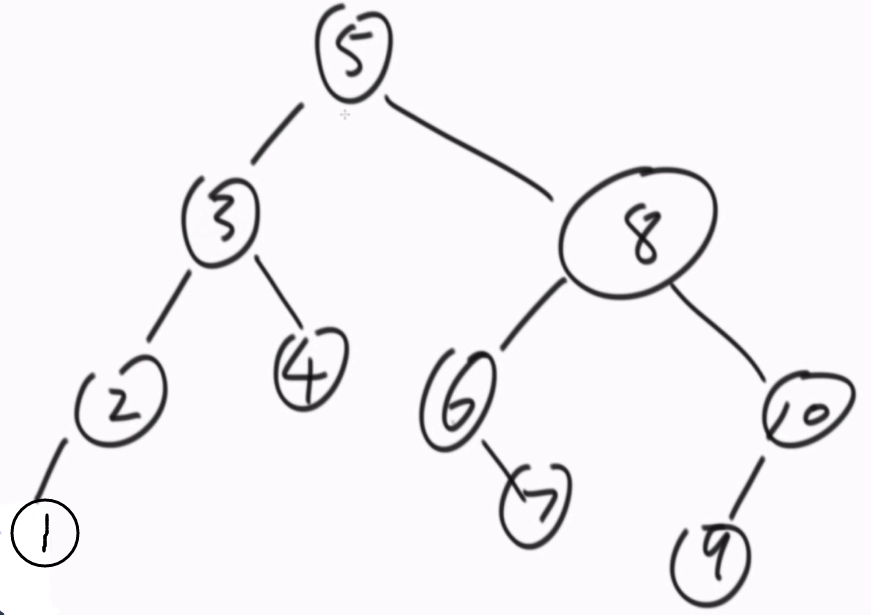
二叉树的中序遍历的节点是依次升序的就是搜索二叉树！

完全二叉树：对于深度为K的，有n个结点的二叉树，当且仅当其每一个结点都与深度为K的满二叉树中编号从1至n的结点一一对应时称之为完全二叉树。

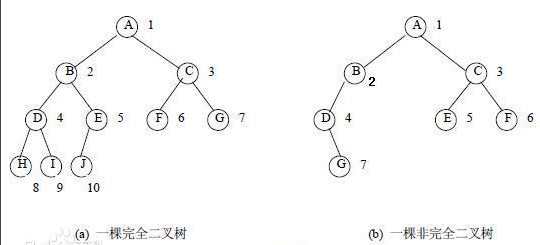
判断逻辑：二叉树按层遍历。

1）一个结点有右孩子，没有左孩子，一定不是完全二叉树。返回false。

2）一个结点只有左孩子没有右孩子 或者 左右孩子都没有，后面遇到的所有结点都必须是叶节点，否则不是完全二叉树，返回false。 

代码实现

 判断搜索二叉树和完全二叉树

题目八

 思路

二叉树实现的堆，没有空间浪费，没有扩容代价。这两个方面比使用数组实现堆更好。

因为时间复杂度的要求，不能用遍历的方式获取。

满二叉树的高度为L ，它的节点个数是2^L -1。

完全二叉树：

①遍历整棵树的左边界，看看左边界最后一个结点到了哪一层。代价是O(logn)。

②遍历头结点x的右子树的左边界，看看右子树的左边界到没到最后一层。

　　如果到了最后一层，说明整棵树的左子树的满的，能够得到整棵树左子树的高度H左，进而得到左子树的节点数，2^H左 -1，加上当前节点，一共是2^H左 个节点。整棵树的右子树也是一颗完全二叉树，递归求出右树的节点数。

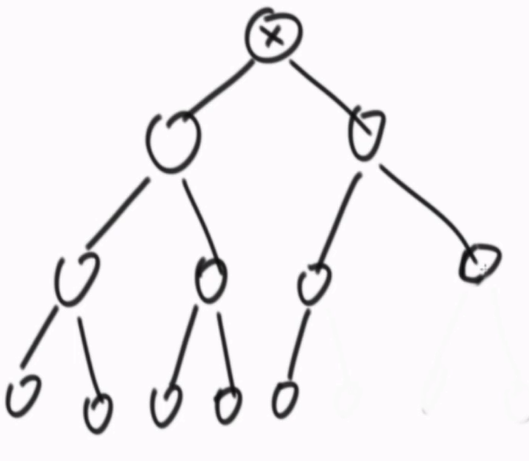
　　如果没到最后一层，说明整棵树的右子树是满的，能够得到整棵树右子树的高度H右，进而得到右子树的节点数，2^H右 -1，加上当前节点，一共是2^H右 个节点。整棵树的左子树也是一颗完全二叉树，递归求出左子树的节点数。

复杂度：

每一层只遍历一个节点 O(logn)，遍历每一个子树的边界O(logn)。

总复杂度 O(logn)*O(logn)。

代码实现

完全二叉树节点的个数