求解数字二进制表示中1的个数?代码如下:
class Program
{
private int Get(int number)
{
if (number == 0) return 0;
if (number == 1) return 1;
return number % 2 + Get(number / 2);
}
static void Main(string[] args)
{
int n=0;
n = Console.Read();
n = (new Program()).Get(n);
Console.Write(n);
Console.ReadKey();
}
}
这个程序的递归实现了某种类型的螺旋状while循环。while循环在循环体每次执行时必须取得某种进展,逐步迫近循环终止条件。递归函数也是如此,它在每次递归调用后必须越来越接近某种限制条件。当递归函数符合这个限制条件时,它便不在调用自身。
递归有什么用呢?其实,递归并不是个好算法,因为在有多次(实际情况很可能是许多许多次)调用递归的情况下,会非常耗内存。因此,我们使用递归算法,必须 权衡运行时间与内存这两者的消耗,一般来说,递归算法不适合解决数学计算!
具体来说,一般递归用于关于二叉树的算法。详见http://www.cnblogs.com/abatei/archive/2008/05/23/1205707.html。
6.2.2 二叉树的存储结构
二叉树的存储可分为两种:顺序存储结构和链式存储结构。
1. 顺序存储结构
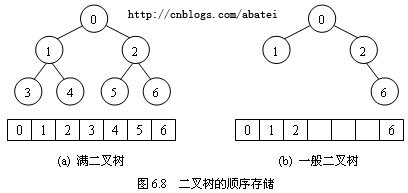
把一个满二叉树自上而下、从左到右顺序编号,依次存放在数组内,可得到图6.8(a)所示的结果。设满二叉树结点在数组中的索引号为i,那么有如下性质。
(1)如果i = 0,此结点为根结点,无双亲。
(2)如果i > 0,则其双亲结点为(i -1) / 2 。(注意,这里的除法是整除,结果中的小数部分会被舍弃。)
(3)结点i的左孩子为2i + 1,右孩子为2i + 2。
(4)如果i > 0,当i为奇数时,它是双亲结点的左孩子,它的兄弟为i + 1;当i为偶数时,它是双新结点的右孩子,它的兄弟结点为i – 1。
(5)深度为k的满二叉树需要长度为2 k-1的数组进行存储。
通过以上性质可知,使用数组存放满二叉树的各结点非常方便,可以根据一个结点的索引号很容易地推算出它的双亲、孩子、兄弟等结点的编号,从而对这些结点进行访问,这是一种存储二叉满二叉树或完全二叉树的最简单、最省空间的做法。
为了用结点在数组中的位置反映出结点之间的逻辑关系,存储一般二叉树时,只需要将数组中空结点所对应的位置设为空即可,其效果如图6.8(b)所示。这会造成一定的空间浪费,但如果空结点的数量不是很多,这些浪费可以忽略。
一个深度为k的二叉树需要2 k-1个存储空间,当k值很大并且二叉树的空结点很多时,最坏的情况是每层只有一个结点,再使用顺序存储结构来存储显然会造成极大地浪费,这时就应该使用链式存储结构来存储二叉树中的数据。
1. 链式存储结构
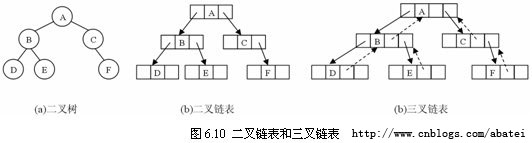
二叉树的链式存储结构可分为二叉链表和三叉链表。二叉链表中,每个结点除了存储本身的数据外,还应该设置两个指针域left和right,它们分别指向左孩子和右孩子(如图6.9(a)所示)。
当需要在二叉树中经常寻找某结点的双亲,每个结点还可以加一个指向双亲的指针域parent,如图6.9(b)所示,这就是三叉链表。

图6.10所示的是二叉链表和三叉链表的存储结构,其中虚线箭头表示parent指针所指方向。
二 叉树还有一种叫双亲链表的存储结构,它只存储结点的双亲信息而不存储孩子信息,由于二叉树是一种有序树,一个结点的两个孩子有左右之分,因此结点中除了存 放双新信息外,还必须指明这个结点是左孩子还是右孩子。由于结点不存放孩子信息,无法通过头指针出发遍历所有结点,因此需要借助数组来存放结点信息。图6.10(a)所示的二叉树使用双亲链表进行存储将得到图6.11所示的结果。由于根节点没有双新,所以它的parent指针的值设为-1。

双亲链表中元素存放的顺序是根据结点的添加顺序来决定的,也就是说把各个元素的存放位置进行调换不会影响结点的逻辑结构。由图6.11可知,双亲链表在物理上是一种顺序存储结构。
二叉树存在多种存储结构,选用何种方法进行存储主要依赖于对二叉树进行什么操作来确定。而二叉链表是二叉树最常用的存储结构,下面几节给出的有关二叉树的算法大多基于二叉链表存储结构。
6.3 二叉树的遍历
二叉树遍历(Traversal)就是按某种顺序对树中每个结点访问且只能访问一次的过程。访问的含义很广,如查询、计算、修改、输出结点的值。树遍历本质上是将非线性结构线性化,它是二叉树各种运算和操作的实现基础,需要高度重视。
6.3.1 二叉树的深度优先遍历
|
图6.12二叉树的递归定义 |
|
D |
|
L |
|
R |
我们是用递归的方法来定义二叉树的。每棵二叉树由结点、左子树、右子树这三个基本部分组成,如果遍历了这三部分,也就遍历了整个二叉树。如图6.12所示,D为二叉树中某一结点,L、R分别为结点D的左、右子树,则其遍历方式有6种:

先左后右 先右后左
先序 DLR DRL
中序 LDR RDL
后序 LRD RLD
这里只讨论先左后右的三种遍历算法。
如图6.13所示,在沿着箭头方向所指的路径对二叉树进行遍历时,每个节点会在这条搜索路径上会出现三次,而访问操作只能进行一次,这时就需要决定在搜索路径上第几次出现的结点进行访问操作,由此就引出了三种不同的遍历算法。

1. 先序遍历
若二叉树为非空,则过程为:
(1)访问根节点。
(2)先序遍历左子树。
(3)先序遍历右子树。
图6.13中,先序遍历就是把标号为(1)的结点按搜索路径访问的先后次序连接起来,得出结果为:ABDECF。
2. 中序遍历
若二叉树为非空,则过程为:
(1)按中序遍历左子树。
(2)访问根结点。
(3)按中序遍历右子树。
图6.13中,先序遍历就是把标号为(2)的结点按搜索路径访问的先后次序连接起来,得出结果为:DBEACF。
3. 后序遍历
若二叉树为非空,则过程为:
(1)按后序遍历左子树。
(2)按后序遍历右子树
(3)访问根结点。
图6.13中,先序遍历就是把标号为(3)的结点按搜索路径访问的先后次序连接起来,得出结果为:DEBFCA。
【例6-1 BinaryTreeNode.cs】二叉树结点类
2 public class Node
3 {
4 //成员变量
5 private object _data; //数据
6 private Node _left; //左孩子
7 private Node _right; //右孩子
8 public object Data
9 {
10 get { return _data; }
11 }
12 public Node Left //左孩子
13 {
14 get { return _left; }
15 set { _left = value; }
16 }
17 public Node Right //右孩子
18 {
19 get { return _right; }
20 set { _right = value; }
21 }
22 //构造方法
23 public Node(object data)
24 {
25 _data = data;
26 }
27 public override string ToString()
28 {
29 return _data.ToString();
30 }
31 }
32
Node类专门用于表示二叉树中的一个结点,它很简单,只有三个属性:Data表示结点中的数据;Left表示这个结点的左孩子,它是Node类型;Right表示这个结点的右孩子,它也是Node类型。
【例6-1 BinaryTree.cs】二叉树集合类
2 public class BinaryTree
3 { //成员变量
4 private Node _head; //头指针
5 private string cStr; //用于构造二叉树的字符串
6 public Node Head //头指针
7 {
8 get { return _head; }
9 }
10 //构造方法
11 public BinaryTree(string constructStr)
12 {
13 cStr = constructStr;
14 _head = new Node(cStr[0]); //添加头结点
15 Add(_head, 0); //给头结点添加孩子结点
16 }
17 private void Add(Node parent, int index)
18 {
19 int leftIndex = 2 * index + 1; //计算左孩子索引
20 if (leftIndex < cStr.Length) //如果索引没超过字符串长度
21 {
22 if (cStr[leftIndex] != '#') //'#'表示空结点
23 { //添加左孩子
24 parent.Left = new Node(cStr[leftIndex]);
25 //递归调用Add方法给左孩子添加孩子节点
26 Add(parent.Left, leftIndex);
27 }
28 }
29 int rightIndex = 2 * index + 2;
30 if (rightIndex < cStr.Length)
31 {
32 if (cStr[rightIndex] != '#')
33 { //添加右孩子
34 parent.Right = new Node(cStr[rightIndex]);
35 //递归调用Add方法给右孩子添加孩子节点
36 Add(parent.Right, rightIndex);
37 }
38 }
39 }
40 public void PreOrder(Node node) //先序遍历
41 {
42 if (node != null)
43 {
44 Console.Write(node.ToString()); //打印字符
45 PreOrder(node.Left); //递归
46 PreOrder(node.Right); //递归
47 }
48 }
49 public void MidOrder(Node node) //中序遍历
50 {
51 if (node != null)
52 {
53 MidOrder(node.Left); //递归
54 Console.Write(node.ToString()); //打印字符
55 MidOrder(node.Right); //递归
56 }
57 }
58 public void AfterOrder(Node node) //后继遍历
59 {
60 if (node != null)
61 {
62 AfterOrder(node.Left); //递归
63 AfterOrder(node.Right); //递归
64 Console.Write(node.ToString()); //打印字符
65 }
66 }
67 }
68
BinaryTree是一个二叉树的集合类,它属于二叉链表,实际存储的信息只有一个头结点指针(Head),由于是链式存储结构,可以由Head指针出发遍历整个二叉树。为了便于测试及添加结点,假设BinaryTree类中存放的数据是字符类型,第5行声明了一个字符串类型成员cStr,它用于存放结点中所有的字符。字符串由满二叉树的方式进行构造,空结点用‘#’号表示(参考本章“二叉树存储结构”这一小节中的“顺序存储结构”)。图6.13所示的二叉树可表示为:“ABCDE#F”。
11~16行的构造方法传入一个构造字符串,并在Add()方法中根据这个字符串来构造二叉树中相应的结点。需要注意,这个构造方法只用于测试。
17~39行的Add()方法用于添加结点,它的第一个参数parent表示需要添加孩子结点的双亲结点,第二个参数index表示这个双亲结点的编号(编号表示使用顺序存储结构时它在数组中的索引,请参考本章“二叉树存储结构”这一小节中的“顺序存储结构”)。添加孩子结点的方法是先计算孩子结点的编号,然后通过这个编号在cStr中取出相应的字符,并构造新的孩子结点用于存放这个字符,接下来递归调用Add()方法给孩子结点添加它们的孩子结点。注意,这个方法只用于测试。
40~48行代码的PreOrder()方法用于先序遍历,它的代码跟之前所讲解的先序遍历过程完全一样。
49~57行代码的MidOrder()方法用于中序遍历。
58~66行代码的AfterOrder()方法用于后序遍历。
以上三个方法都使用了递归来完成遍历,这符合二叉树的定义。
【例6-1 Demo6-1.cs】二叉树深度优先遍历测试
2 class Demo6_1
3 {
4 static void Main(string[] args)
5 { //使用字符串构造二叉树
6 BinaryTree bTree = new BinaryTree("ABCDE#F");
7 bTree.PreOrder(bTree.Head); //先序遍
8 Console.WriteLine();
9 bTree.MidOrder(bTree.Head); //中序遍
10 Console.WriteLine();
11 bTree.AfterOrder(bTree.Head); //后序遍
12 Console.WriteLine();
13 }
14 }
15
运行结果:
ABDECF
DBEACF
DEBFCA
6.3.2 二叉树的宽度优先遍历
之前所讲述的二叉树的深度优先遍历的搜索路径是首先搜索一个结点的所有子孙结点,再搜索这个结点的兄弟结点。是否可以先搜索所有兄弟和堂兄弟结点再搜索子孙结点呢?
由于二叉树结点分属不同的层次,因此可以从上到下、从左到右依次按层访问每个结点。它的访问顺序正好和之前所述二叉树顺序存储结构中的结点在数组中的存放顺序相吻合。如图6.13中的二叉树使用宽度优先遍历访问的顺序为:ABCDEF。
这个搜索过程不再需要使用递归,但需要借助队列来完成。
(1)将根结点压入队列之中,开始执行步骤(2)。
(2)若队列为空,则结束遍历操作,否则取队头结点D。
(3)若结点D的左孩子结点存在,则将其左孩子结点压入队列。
(4)若结点D的右孩子结点存在,则将其右孩子结点压入队列,并重复步骤(2)。
【例6-2 BinaryTreeNode.cs.cs】二叉树结点类,使用例6-1同名文件。
【例6-2 LevelOrderBinaryTree.cs】包含宽度优先遍历方法的二叉树集合类
打开例6-1的【BinaryTree.cs】文件,在BinaryTree类中添加如入方法后另存为LevelOrderBinaryTree.cs文件。
2 {
3 Queue queue = new Queue(); //声明一个队例
4 queue.Enqueue(_head); //把根结点压入队列
5 while (queue.Count > 0) //只要队列不为空
6 {
7 Node node = (Node)queue.Dequeue(); //出队
8 Console.Write(node.ToString()); //访问结点
9 if (node.Left != null) //如果结点左孩子不为空
10 { //把左孩子压入队列
11 queue.Enqueue(node.Left);
12 }
13 if (node.Right != null) //如果结点右孩子不为熔
14 { //把右孩子压入队列
15 queue.Enqueue(node.Right);
16 }
17 }
18 }
【例6-2 Demo6-2.cs】二叉树宽度优先遍历测试
2 class Demo6_2
3 {
4 static void Main(string[] args)
5 { //使用字符串构造二叉树
6 BinaryTree bTree = new BinaryTree("ABCDE#F");
7 bTree.LevelOrder();
8 }
9 }
运行结果:ABCDEF