Gerald got a very curious hexagon for his birthday. The boy found out that all the angles of the hexagon are equal to 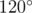 . Then he measured the length of its sides, and found that each of them is equal to an integer number of centimeters. There the properties of the hexagon ended and Gerald decided to draw on it.
. Then he measured the length of its sides, and found that each of them is equal to an integer number of centimeters. There the properties of the hexagon ended and Gerald decided to draw on it.
He painted a few lines, parallel to the sides of the hexagon. The lines split the hexagon into regular triangles with sides of 1 centimeter. Now Gerald wonders how many triangles he has got. But there were so many of them that Gerald lost the track of his counting. Help the boy count the triangles.
The first and the single line of the input contains 6 space-separated integers a1, a2, a3, a4, a5 and a6 (1 ≤ ai ≤ 1000) — the lengths of the sides of the hexagons in centimeters in the clockwise order. It is guaranteed that the hexagon with the indicated properties and the exactly such sides exists.
Print a single integer — the number of triangles with the sides of one 1 centimeter, into which the hexagon is split.
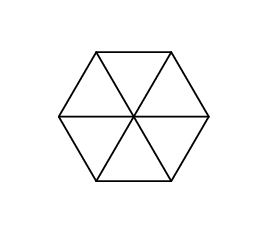
1 1 1 1 1 1
6
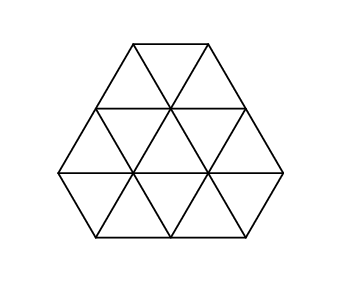
1 2 1 2 1 2
13
This is what Gerald's hexagon looks like in the first sample:
And that's what it looks like in the second sample:
解:
取不相邻的三条边以边长向外即可扩展成一个大等边三角形,因为边长为n的大三角形由n*n个小单位角形拼成,更容易计算。,再减去补上的三角形面积。
这是我搜的题解,补的方法很巧妙。

#include <cstdio> #include <iostream> #include <algorithm> #define N 1000005 using namespace std; int main() { int a[7]; for(int i = 0; i < 6; i++) scanf("%d", &a[i]); printf("%d", (a[0] + a[1] + a[2]) * (a[0] + a[1] + a[2]) - (a[0] *a[0] + a[2] * a[2] + a[4] * a[4])); return 0; }
