第八章 线性时间排序
比较排序算法的下界
把比较排序的每次比较当做决策树中的每个决策分支。每个结点都是到达排好序时原始输入的下标数组。原始输入N个数有N!种排序。所以决策树至少有N!个结点。
考虑一棵高度为h,具有l个可达结点的决策树,它对应一个对N个元素所做的比较排序。我们有:

得到:
所以在最坏情况下,任何比较排序算法都需要做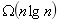 次比较。
次比较。
堆排序和归并排序都是渐近最优的比较排序算法。
计数排序
计数排序假设n个输入元素的每一个都是在0到k区间[0,k]内的一个整数,其中k为某个整数。当k=O(n)时,排序的运行时间为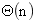 。
。
|
#!/usr/bin/env python #encoding=utf-8 import random def count_sort(A,B,k): C = [0 for i in range(0,k+1)] for j in range(0,len(A)): C[A[j]] += 1 for i in range(1,k+1): C[i] += C[i-1] for j in range(len(A)-1,-1,-1): B[C[A[j]]-1] = A[j] C[A[j]] += -1 A = [int(random.random()*10) for i in range(0,100)] B = [0 for i in range(0,100)] count_sort(A,B,9) print(B) |
基数排序
https://baike.baidu.com/item/%E5%9F%BA%E6%95%B0%E6%8E%92%E5%BA%8F/7875498?fr=aladdin
从低位到高位排序,高位排序的过程中运用到了低位已经排好的结果。
|
#!/usr/bin/env python #encoding=utf-8 import math def sort(a, radix=10): """a为整数列表, radix为基数""" K = int(math.ceil(math.log(max(a), radix))) # 用K位数可表示任意整数 bucket = [[] for i in range(radix)] # 不能用 [[]]*radix for i in range(1, K+1): # K次循环 for val in a: bucket[int(val%(radix**i)/(radix**(i-1)))].append(val) # 析取整数第K位数字 (从低到高) del a[:] for each in bucket: a.extend(each) # 桶合并 bucket = [[] for i in range(radix)] a = list(range(99,0,-1)) sort(a,10) print(a) |
桶排序
桶排序:假设输入数据服从均匀分布,平均情况下它的时间代价为O(n)。
|
#!/usr/bin/env python #encoding=utf-8 import random import math def insertion_sort(A): for j in range(1,len(A),1): key = A[j] i = j-1 while i >= 0 and A[i] > key: A[i+1] = A[i] i = i-1 A[i+1] = key def bucket_sort(A): n = len(A) B = [] V = [[] for i in range(0,n)] for i in range(0,len(A)): V[math.floor(n*A[i])].append(A[i]) for a in V: insertion_sort(a) for a in V: B.extend(a) print(B) A = [random.random() for i in range(0,88)] print(A) bucket_sort(A) |
第九章 中位数和顺序统计量
输入:一个包含n个数的集合A和一个整数i,1<=i<=n.
输出:元素x属于A,且A中恰好有i-1个其他元素小于它。
期望为线性时间的选择算法
和快速排序一样,进行递归划分。
|
#!/usr/bin/env python # -*- coding:UTF-8 -*- def partition(A,p,r): x = A[r] i = p-1 for j in range(p,r): if A[j]<=x: i += 1 tmp = A[i] A[i] = A[j] A[j] = tmp tmp = A[i+1] A[i+1] = A[r] A[r] = tmp return i + 1 def quick_sort(A,p,r): if p < r: q = partition(A,p,r) quick_sort(A,p,q-1) quick_sort(A,q+1,r) def randomized_select(A,p,r,i): if p==r: return A[p] q = partition(A,p,r) k= q-p+1 if i == k: return A[q] elif i < k: return randomized_select(A,p,q-1,i) else: return randomized_select(A,q+1,r,i-k) if __name__ == '__main__': A = [9,3,5,2,3,5,7,8,9,1,11,20,0,2] B=A[:] print(A) quick_sort(A,0,len(A)-1) print(A) selected = 9 i = randomized_select(B,0,len(B)-1,selected) print(i,A[selected-1]) |
最坏情况为线性时间的选择算法
|
#!/usr/bin/env python # -*- coding:UTF-8 -*- import random import math subLen = 5 midSub = 2 def select_insertion_sort(A,start,end): for j in range(start+1,end+1,1): key = A[j] i = j-1 while i >= start and A[i] > key: A[i+1] = A[i] i = i-1 A[i+1] = key def select_partition(A,p,r,x): i = p for j in range(p,r+1): if A[j]<=x: tmp = A[i] A[i] = A[j] A[j] = tmp i += 1 return i-p def select(A,start,end,s): if end-start+1 <= subLen: select_insertion_sort(A,start,end) return A[start+s-1] c = math.ceil((end-start+1)/subLen) B = [] for i in range(0,c): E = (i*start + subLen-1) if (i*start + subLen-1) < (len(A)-1) else (len(A)-1) select_insertion_sort(A,start+i*subLen,E) midIndex = (start+i*subLen+midSub) if (i < c-1) else int((start+i*subLen+end)/2) B.append(A[midIndex]) b = select(B,0,len(B)-1,math.ceil(len(B)/2)) k = select_partition(A,start,end,b) if k == s: return b elif k > s: return select(A,start,start+k-1,s) else: return select(A,start+k,end,s-k) if __name__ == '__main__': A = [int(random.random()*1000) for i in range(0,400)] C = A[:] A.sort() s = 117 value = select(C,0,len(C)-1,s) print(value,A[s-1]) |