算法导论Ch4

分治策略

最大子数组问题

A = [13,-3,-25,20,-3,-16,-23,18,20,-7,12,-5,-22,15,-4,7]

暴力解法：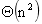

分治方法：

将数组划分为两个规模尽量相等的子数组。最大子数组A[i..j]位置必然是：

完全在A[low,mid]中;

完全在A[mid+1,high]中;

跨越了中点，因此low<=i<=mid<=j<=high.

#!/usr/bin/env python

# -*- coding:UTF-8 -*-

import math

A = [13,-3,-25,20,-3,-16,-23,18,20,-7,12,-5,-22,15,-4,7]

def findMaxCrossingSubarray(A,low,mid,high):

    leftSum = -float("inf")

    SUM = 0

    maxLeft = mid

    for i in range(mid,low-1,-1):

        SUM += A[i]

        if SUM > leftSum:

            leftSum = SUM

            maxLeft = i

            

    rightSum = -float("inf")

    SUM = 0

    maxRight = mid+1

    for j in range(mid+1,high+1,1):

        SUM += A[j]

        if SUM > rightSum:

            rightSum = SUM

            maxRight = j

    return (maxLeft,maxRight,leftSum+rightSum)

def findMaximumSubarray(A,low,high):

    if low == high:

        return (low,high,A[low])

    else:

        mid = math.floor((low+high)/2)

        (leftLow,leftHigh,leftSum)=findMaximumSubarray(A,low,mid)

        (rightLow,rightHigh,rightSum)=findMaximumSubarray(A,mid+1,high)

        (crossLow,crossHigh,crossSum)=findMaxCrossingSubarray(A,low,mid,high)

        if leftSum >= rightSum and leftSum >= crossSum:

            return (leftLow,leftHigh,leftSum)

        elif rightSum >= leftSum and rightSum >= crossSum:

            return (rightLow,rightHigh,rightSum)

        else:

            return (crossLow,crossHigh,crossSum)

if __name__ == '__main__':

    result = findMaximumSubarray(A,0,len(A)-1)

    print(result)

线性时间算法：

#!/usr/bin/env python

# -*- coding:UTF-8 -*-

A = [13,-3,-25,20,-3,-16,-23,18,20,-7,12,-5,-22,15,-4,7]

'''

https://www.cnblogs.com/allzy/p/5162815.html

如果累加和出现小于0的情况，  

则和最大的子序列肯定不可能包含前面的元素，  

这时将累加和置0，从下个元素重新开始累加

'''

def findMaximumSubarrayLinearAlgo(A):

    maxSum = 0

    thisSum = 0

    maxLeft = 0

    maxRight = 0

    for i in range(0,len(A)):

        thisSum += A[i]

        if thisSum > maxSum:

            maxRight = i

            maxSum = thisSum

        elif thisSum < 0:

            thisSum = 0

            maxLeft = i+1

    return (maxLeft,maxRight,maxSum) if maxSum >0 else None

if __name__ == '__main__':

    result = findMaximumSubarrayLinearAlgo(A)

    print(result)

后语：

从暴力解法到分治算法，是学以致用。

有线性时间算法，提示每个问题可能有更妙的解决办法。

矩阵乘法

常规方法：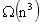

Strassen算法：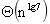

通过中间过程的精妙优化，将运行时间的递归式由(1)变成(2)

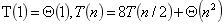    (1)

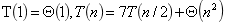   (2)

后语：

就像书上说的，最初可能认为矩阵乘法都要花费时间，但通过看到Strassen算法，才看到算法的精妙。

求解递归式*

迭代法

递归树

主方法

Akra-Bazzi方法