1.排序时,数组含有大量重复元素,应该使用哪种排序手段?
(1)mergeSort:与数组的特征无关,比较次数总是在1/2NlgN~NlgN之间
(2)quickSort:当所有的元素全都相同的时候,使用平方次时间
2.3-way partitioning算法的目标:
将数组划分为3部分:
(1)lt和gt之间的元素等于v
(2)lt的左边元素小于v
(3)gt的右边元素大于v
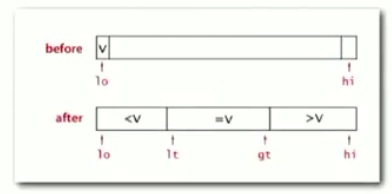
3.Dijkstra的3-way partitioning算法:
(1)划分元素v是a[lo]
(2)scan i from left to right
①a[i]<v:交换a[i]和a[lt],同时增大lt和i
②a[i]>v:交换a[i]和a[gt],减小gt
③a[i]==v:增大i(也就是不移动相等的元素)
i指向未遍历的元素,lt左边是比v小的,gt右边是比v大的,lt与i之间的是等于v的元素。
这个操作保证了等于v的元素 in place,接下来只需要分别对大于v和小于v的两个部分分别排序。

4.如果打乱数组,并且使用3-way partitioning,很多应用运行时间会是线性时间,会比mergesort快很多。
5.算法实现
package com.cx.sort; public class Quick3way { public static void sort(Comparable[] a) { //打乱数组 Shuffling.sort(a); sort(a,0,a.length-1); } public static void sort(Comparable[] a,int lo,int hi) { if(hi<=lo) return; int lt=lo,gt=hi,i=lo; Comparable v=a[lo]; //只要i和gt不重叠就要继续进行 //完成后,lt左边小于v,gt右边大于v,lt..gt等于v while(i<=gt) { int cmp=a[i].compareTo(v); //a[i]<v,交换a[lt]和a[i] if(cmp<0) exch(a, i++, lt++); //a[i]>v,交换a[i]和a[gt] else if(cmp>0) exch(a, i, gt--); //保证等于v的元素in place else i++; } //递归排序lt左侧和gt右侧部分 sort(a, lo, lt-1); sort(a, gt+1, hi); } private static boolean less(Comparable v,Comparable w) { return v.compareTo(w)<0; } private static void exch(Comparable[] a,int i ,int j ) { Comparable t=a[i]; a[i]=a[j]; a[j]=t; } private static void show(Comparable[] a) { for(int i=0;i<a.length;i++) { System.out.print(a[i]+" "); } System.out.println(); } public static void main(String[] args) { String a[]= {"s","o","r","t","e","x","a","m","p","l","e"}; show(a); sort(a); show(a); } }