手动博客搬家: 本文发表于20170716 10:58:18, 原地址https://blog.csdn.net/suncongbo/article/details/81061601
https://www.lydsy.com/JudgeOnline/problem.php?id=1179
题意:给定一张有向图,点有点权。给定起点(仅一个)(s)与终点集合(多个)(T),问开始于起点、结束于终点集合中的一个点的路径中点权和的最大值。
题解:这里,第一步当然是tarjan缩点。
由于是开始于特定点,dp有些麻烦,建议采用spfa. 但是DP也能做,而且bfs和dfs都能做。只不过,有一些需要注意的地方,很容易写错。
bfs状态转移方程很简单:(dp[i])表示从s出发到i这个点路径点权和的最大值,(dp[i]=max_{jin ind[i]}{dp[j]+a[i]}), a[i]为点权。对于终点集合,我们可以建一个超级终点,每一个终点向超级终点连边,当然也可以朴素地枚举每个终点。但是,有一个细节问题坑了我很久:如果是这样写的:
Tarjan原图中的每一个点;
建新图;
bfs(); (队列中初始只有一个元素s)
ans = dp[超级终点];
则必然会WA. 后来我又对着标程查了好久,问了几位大佬,最后实在没办法对拍了一下,发现生成了这样一组数据成功卡掉自己,经简化如下——
3 2
1 2
3 2
5
1
3
1 1
2
Read 0,Expected 6.
正确的写法应该是:
Tarjan(s); //从s能到达的点
建新图;
bfs(); (队列中初始只有一个元素s)
ans = dp[超级终点];
只有第一行tarjan不一样。为什么呢?
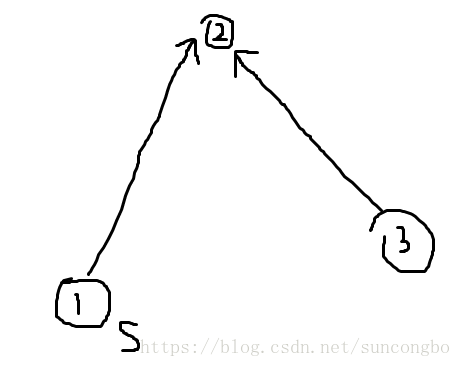
原因是:对于一个点i, 刚才我们讨论的数食物链、字母最多出现次数、最长路径,都是要求(i)的所有入边的起点都被更新后才可转移(i)(将其加入队列),bfs的时候从所有入度为0的点开始。但是,现在情况变了,如果我们只从s开始bfs,有一些s走不到的点将永远不会被更新,这样这个点所连向的边也不会被更新,就相当于这个点作废了。但是实际上这个点并未作废。如图所示,如果1号点为起点,2号点为终点,那3号点显然不会被访问到,但是由于2号点有1->2, 3->2两条入边,因此3号点不更新,2号点永远也不会被更新,答案一直是0.但是实际上,2还应该被1更新,因为起点1一定可以通过1->2进入2号点。
实际上,我们确保这种入边的起点先统计的顺序,原因是防止一个点有许多条转移的途径,但是只枚举了其中的一部分,最优解藏在另一部分中的这种情况。但是在这里,所谓“另一部分”是s点永远不可能达到的,因此答案为0,不可能成为最优解,反而还会拖累2号点的更新。
AC代码:
#include<cstdio>
#include<algorithm>
using namespace std;
const int N = 500000;
struct Edge
{
int v,nxt; bool us;
} e[N+2],e0[N+2];
int fe[N+2],fe0[N+2];
int a[N+2],a0[N+2];
bool f[N+2];
int dfn[N+2],low[N+2];
int sta[N+2];
bool ins[N+2];
int clr[N+2];
int dp[N+2];
int que[N+2];
int ind[N+2];
bool f0[N+2];
int n,m,m0,s,p,tp,cnt,num;
void addedge(int u,int v)
{
m++; e[m].v = v;
e[m].nxt = fe[u]; fe[u] = m;
}
void addedge0(int u,int v)
{
m0++; e0[m0].v = v; ind[v]++;
e0[m0].nxt = fe0[u]; fe0[u] = m0;
}
void Tarjan(int u)
{
cnt++; dfn[u] = low[u] = cnt; ins[u] = true;
tp++; sta[tp] = u;
for(int i=fe[u]; i; i=e[i].nxt)
{
if(dfn[e[i].v]==0) {Tarjan(e[i].v); low[u] = min(low[u],low[e[i].v]);}
else if(ins[e[i].v]==true) {low[u] = min(low[u],dfn[e[i].v]);}
}
if(low[u]==dfn[u])
{
num++; clr[u] = num; a0[num] = a[u]; f0[num] = f[u];
while(sta[tp]!=u)
{
ins[sta[tp]] = false;
clr[sta[tp]] = num;
a0[num] += a[sta[tp]];
f0[num] = f[sta[tp]]||f0[num];
tp--;
}
ins[u] = false; tp--;
}
}
void bfs()
{
int head = 1,tail = 1; que[tail] = clr[s]; dp[clr[s]] = a0[clr[s]];
while(head<=tail)
{
int cur = que[head]; head++;
for(int i=fe0[cur]; i; i=e0[i].nxt)
{
if(e0[i].us==false)
{
ind[e0[i].v]--; e0[i].us = true; dp[e0[i].v] = max(dp[e0[i].v],dp[cur]+a0[e0[i].v]);
if(ind[e0[i].v]==0)
{
tail++; que[tail] = e0[i].v;
}
}
}
}
}
int main()
{
int mm; m = 0; scanf("%d%d",&n,&mm);
for(int i=1; i<=mm; i++)
{
int x,y; scanf("%d%d",&x,&y); addedge(x,y);
}
for(int i=1; i<=n; i++) scanf("%d",&a[i]);
scanf("%d%d",&s,&p);
for(int i=1; i<=p; i++) {int x; scanf("%d",&x); f[x] = true;}
cnt = 0; Tarjan(s);
//for(int i=1; i<=n; i++) if(!dfn[i]) Tarjan(i);
num++;
for(int i=1; i<=n; i++)
{
for(int j=fe[i]; j; j=e[j].nxt)
{
if(clr[i]!=0 && clr[e[j].v]!=0 && clr[i]!=clr[e[j].v])
{
addedge0(clr[i],clr[e[j].v]);
}
}
}
for(int i=1; i<=num; i++) {if(f0[i]==true) addedge0(i,num);}
bfs();
printf("%d
",dp[num]);
return 0;
}
dfs当然也能做,此处不再赘述。