哈夫曼树定义
(01) 路径和路径长度
定义:在一棵树中,从一个结点往下可以达到的孩子或孙子结点之间的通路,称为路径。通路中分支的数目称为路径长度。若规定根结点的层数为1,则从根结点到第L层结点的路径长度为L-1。
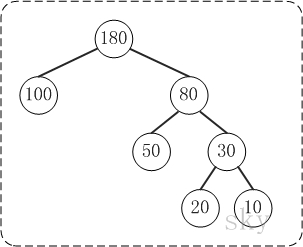
例子:100和80的路径长度是1,50和30的路径长度是2,20和10的路径长度是3。
(02) 结点的权及带权路径长度
定义:若将树中结点赋给一个有着某种含义的数值,则这个数值称为该结点的权。结点的带权路径长度为:从根结点到该结点之间的路径长度与该结点的权的乘积。
例子:节点20的路径长度是3,它的带权路径长度= 路径长度 * 权 = 3 * 20 = 60。
(03) 树的带权路径长度
定义:树的带权路径长度规定为所有叶子结点的带权路径长度之和,记为WPL。
例子:示例中,树的WPL= 1*100 + 2*80 + 3*20 + 3*10 = 100 + 160 + 60 + 30 = 350。
哈夫曼树
哈夫曼树又称最优二叉树。它是 n 个带权叶子结点构成的所有二叉树中,带权路径长度 WPL 最小的二叉树。
哈夫曼树的构造过程:
- 给定的n个权值{W1,W2,…,Wn}构造n棵只有一个叶结点的二叉树,从而得到一个二叉树的集合F={T1,T2,…,Tn}。
- 在F中选取根结点的权值最小和次小的两棵二叉树作为左、右子树构造一棵新的二叉树,这棵新的二叉树根结点的权值为其左、右子树根结点权值之和。
- 在集合F中删除作为左、右子树的两棵二叉树,并将新建立的二叉树加入到集合F中。
- 重复(2)、(3)两步,当F中只剩下一棵二叉树时,这棵二叉树便是所要建立的哈夫曼树。

哈夫曼编码
规定哈夫曼树中的左分支为0,右分支为1,则从根结点到每个叶结点所经过的分支对应的0和1组成的序列便为该结点对应字符的编码。这样的编码称为哈夫曼编码

注意:在一组字符的哈夫曼编码中,不可能出现一个字符的哈夫曼编码是另一个字符哈夫曼编码的前缀。
测试代码
1 #include<stdio.h> 2 #include<string.h> 3 #define N 50 4 #define M 2*N - 1 5 typedef struct 6 { 7 char data[5]; //节点值 8 int weight; //权重 9 int parent; //双亲节点 10 int lchild; //左孩子 11 int rchild; //右孩子 12 }HTNode; 13 14 typedef struct 15 { 16 char cd[N]; //存放哈夫曼编码 17 int start; //ch[start....n]存放哈夫曼编码 18 }HCode; 19 20 void CreateHT(HTNode ht[], int n) 21 { 22 int i, k, node1, node2; 23 int min1, min2; 24 for (i = 0; i < 2 * n - 1; ++i) 25 ht[i].parent = ht[i].lchild = ht[i].rchild = -1; 26 for (i = n; i < 2 * n - 1; ++i) 27 { 28 min1 = min2 = 32767; //min1最小,min2次小; 29 node1 = node2 = -1; 30 for (k = 0; k <= i - 1; ++k) 31 if (ht[k].parent == -1) 32 { 33 if (ht[k].weight < min1) 34 { 35 min2 = min1; 36 node2 = node1; 37 min1 = ht[k].weight; 38 node1 = k; 39 } 40 else if (ht[k].weight < min2) 41 { 42 min2 = ht[k].weight; 43 node2 = k; 44 } 45 } 46 ht[node1].parent = i; //合并两个最小的和次小的节点 47 ht[node2].parent = i; 48 ht[i].weight = ht[node1].weight + ht[node2].weight; 49 ht[i].lchild = node1; 50 ht[i].rchild = node2; 51 } 52 } 53 54 void CreateHCode(HTNode ht[], HCode hcd[], int n) 55 { 56 int i, f, c; 57 HCode hc; 58 for (i = 0; i < n; ++i) 59 { 60 hc.start = n; 61 c = i; 62 f = ht[i].parent; 63 while (f != -1) 64 { 65 if (ht[f].lchild == c) 66 hc.cd[hc.start--] = '0'; 67 else 68 hc.cd[hc.start--] = '1'; 69 c = f; 70 f = ht[f].parent; 71 } 72 hc.start++; 73 hcd[i] = hc; 74 } 75 } 76 77 void DispHCode(HTNode ht[], HCode hcd[], int n) 78 { 79 int i, k; 80 int sum = 0, m = 0, j; 81 for (i = 0; i < n; ++i) 82 { 83 j = 0; 84 printf(" %s: ", ht[i].data); 85 for (k = hcd[i].start; k <= n; ++k) 86 { 87 printf("%c", hcd[i].cd[k]); 88 ++j; 89 } 90 printf(" "); 91 m += ht[i].weight; 92 sum += ht[i].weight*j; 93 } 94 printf(" 平均长度 = %g ", 1.0 * sum / m); 95 } 96 97 int main() 98 { 99 int n = 15, i; 100 const char *str[] = { "The", "of", "a", "to", "and", "in", "that", "he", "is", "at", "on", "for", "His", "are", "be" }; //节点值 101 int fnum[] = { 1192, 677, 541, 518, 462, 450, 242, 195, 190, 181, 174, 157, 138, 124, 123 }; //权重 102 HTNode ht[M]; 103 HCode hcd[M]; 104 for (i = 0; i < n; ++i) 105 { 106 strcpy(ht[i].data, str[i]); 107 ht[i].weight = fnum[i]; 108 } 109 110 CreateHT(ht, n); //创建哈夫曼树 111 CreateHCode(ht, hcd, n); //构造哈夫曼编码 112 DispHCode(ht, hcd, n); //输出哈夫曼编码 113 return 0; 114 }